Every nice maths olympiad algebra problem | Can you solve for a+b=? | Algebra

In this video, I'll be showing you step by step on how to solve this Olympiad Maths Exponential problem using a simple trick.
Please feel free to share your ideas in the comment section.
And if you are new here and you enjoy my content, please hit the like button and subscribe to my channel. Don't forget to hit the bell icon as well so you don't miss on my upcoming videos.

[@damyankorena]

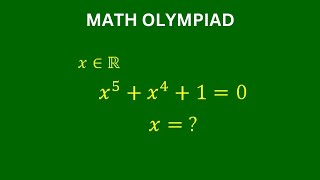
I am bored so lets solve with complex numbers.
4+4i=a²+2abi-b²=(a+bi)²
a+bi=√(4+4i)
Let z=4+4i
|z|=4√2
z/|z|= 1/√2 + i/√2
Arg(z)=π/4
Therefore
√z=2∜2 * e^(πi/8)
Which as shown earlier is equal to a+bi.
a=Re(√z), b=Im(√z)
a=2∜2 * sin(π/8)
b=2∜2 * cos(π/8)
a+b=2∜2 * √2 sin(⅜π)
a+b= 2^(¾) * √(2+√2)
а+b=2√(1+√2)
Naturally while taking the square root of z instead of
Arg(√z)=⅛π we can use
Arg(√z)=⅝π which will by similar methods turn out to be the other solution in which
a+b=-2√(1+√2)

[@ohiyo_o7637]

My approach is:
(a+b)(a-b)=4
(a^2+b^2+4)(a^2+b^2-4)=16
(a^2+b^2)^2=32
a^2+b^2=4root(2) (notice that a^2 and b^2 are both positive, so no plus or minus sign is needed for this square root)
(a+b)^2=4root(2)+4
a+b=plus or minus 2root((root(2)+1))

[@ohiyo_o7637]

i got a+b = root( root(32)+4 ), is it correct or where did i do it wrong

[@ohiyo_o7637]

oh it is the same thing, i just didnt simplify it, i am not very good at math haha

[@damyankorena]

√32=4√2
So
√(4+√32)=√(4+4√2)
= 2√(1+√2)
Therefore they are equal

[@ohiyo_o7637]

I see, thank you