Відео

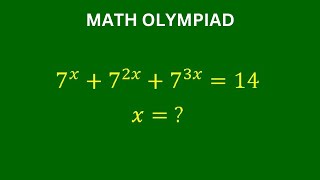
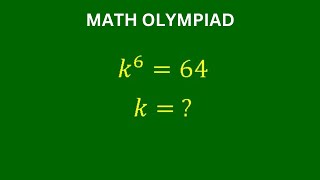
Check 61+y^3 for y=1, 2, 3, 4, bingo! 5^3-4^3 = 61, hence (x,y)=(5,4) or (-4,-5). This is not an IMO-class problem.

Step one and step two can be done in one go you don't have to do every tiny operation

(7^x)+[7^(2x)]+7^(3x)=14 (7^x)+(7^x)²+(7^x)³=2+4+8 =2+2²+2³ As the structure of bot side is similar 7^x=2 --> x=⁷log(2) where the logarithm is 7-based. For other possibile roots, knowing that [(7^x)-2] is a factor, we can factor the equation as (7^x)³+(7^x)²+(7^x)-14=0 [(7^x)-2][(7^x)²+3(7^x)+7]=0 (7x^x)²+3(7^x)+7=0 is a quadratic equation which is positive definite. The roots are imaginary: 7^x=½[-3±isqrt(19)] Have to take logarithm to find x, which can't be done.

How do we know a quartic equation without a cubic can be factorised as (x²+x+p)(x²-x+q) and does it still hold true even when there is a cubic? Also is there any reasoning why the coefficient of x equals 1 anyway? 😄

Notice that in the video, I only considered the positive factors of 61. You can try the negative factors of 61 and show us what you've got. ❤

First❤❤❤❤

Easier with the polar writing. Set i = (1,pi/2 + 2k.pi) with k = 0 or 1. Then for k = 0 ==> sqrt(i) = (1,pi/4) = (sqrt(2)/2).(1 + i) for k = 1 ==> sqrt(i) = (1,pi/4 + pi) = (-sqrt(2)/2).(1 + i)

(√a+√-a)^2=32^2;=>a+2(√a√-a)-a= 1024;=>2(√a√-a)= 1024;=> √(-a^2)= 512;=> a=±512i

Hoc est x= log 2/ log7, Eheu! Responsi. 😂😅😊😢🎉😂😅😊😮😢

At about 4:30 the lecturer is cheating: The tentative factorization over the integers must take the form (x^2+rx+p)(x^2-rx+q) There is no stated prior reason why r should equal 1 (except by already knowing the result)! With r unknown a completely different solution strategy must be adopted, based on all possible factorizations of the constant term.

Introduce y=√(x+5), and rewrite equation as x^2 - y = 5 y^2 - x = 5 Subtract to find x^2 -y^2+x-y=(x-y)(x+y+1)=0. Case y=x => (after squaring) (x-1/2)^2 = 5+1/4 = 21/4 x=(1+√21)/2 is a valid solution, x=(1-√21)/2 is not a valid expression for y as a square root. Case y=-(x+1) => (after squaring) (x+1/2)^2 = 5-1+1/4 = 17/4 x=-(1+√17)/2 is a valid solution. x=(-1+√17)/2 does not lead to a valid expression for y as a square root.

Let a=±bi where b is real. Then √2√b/2=16. Thus, √b=16√2, b=2*16^2=512, and a=±512i

为什么能展开成这两个二次方程的乘积 我随便写了个方程，就无法这样做 x^4 -22x^2+3x+8=0

(x-3)^4=16 x=5 5 - 3 = 2 2^4 =16

What is the value of “log of a complex number” ? Are there any definition of it value?

much simpler in polar coordinates. x⁶≉2⁶ exp(i2nπ) x=2exp(iπ2n/6) =2exp(iθ) θ=0, π/3, 2π/3, π, 4π/3, 5π/3. note exp(iθ)= cosθ +isinθ so solutions are x=±2, 2(cos60±isin60), 2( cos120±isin120) x=±2, 1±i√3 , −1±i√3 it helps to draw the solutions on the Argand diagram. The solutions are six equally spaced points on a circle radius 2

I tried x^4-14x+5x+30=0, using your method, but the system of equations was q-p=5, q+p=-13 and qp=30. Two of the solutions involved quadratics with “c” that contained a square root for a coefficient.

(X^2 - Y^2) = (X+Y)(X-Y)=24; 24=12x2, the sum of X+Y and X-Y is 2X = 14 and X= 7 and Y= 5. This is the answer in natural numbers

It’s tricky, but not as hard as partial fractions.

(x^2)^2 ➖(5)^2={x^4 ➖ 25}=21 3^7 3^7^1 3^1^1 3^1 (x ➖ 3x+1). {x+x ➖ }+{5+5 ➖ }={x^2+10}=10x^2 5^5x^2 2^3^2^3x^2 1^1^1^3x^2 3x^2 (x ➖ 3x+2).

(x⁸ - x²)/(x⁴ - x²) = 9 , (x⁴ - x²) ≠ 0 -> x ≠ 0, ±1 (x⁶ - 1)/(x² - 1) = 9 x⁴ + x² + 1 = 9 x⁴ + x² - 8 = 0 x² = (-1 ± √33)/2 = 2*(-1 ± √33)/4 x = ±√2*√(√33-1)/2, ±i*√2*√(√33+1)/2

La equis subuno en positiva mayor que cero la que es negativa es la equis subidos

One obvious solution is x = ln(2)/ln(7).

let u=7^x , u^3+u^2+u-14=0 , (u-2)(u^2+3u+7)=0 , u=2 , 7^x=2 , x=log2/log7 , 1 -2 test , 7^x+7^2x+7^3x=2+4+8 , --> 14 , OK , 3 -6 /u^2+3u+7=0 , u=(-3+/-V(9-28))/2 , u=(-3+/-i*V(19))/2/ , 7 -14

{14+28x^2+21x^3}=63x^4 14 2^14x^2+3^7x^3 2^7x^2+2^3^7x^3+ 1^1+1^1x^1+ 1^3^4x^1 3^2^2 x^1 3^1^2x^1 3^2x (x ➖ 3x+2).

7ˣ = 2 (2 + 4 + 8 = 14) x = log₇2

X=log2/ log7 (log 2 with base 7)

For logs, you would save steps if you use the log base that cancels out leaving with whatever is in the exponent. In this case, the extra steps would not have been necessary had you simply introduced the log to base 7 on both sides of the equation.

7^x+7^2x+7^3x=14 (7^x)³+(7^x)²+7^x-14=0 Let y=7^x y³+y²+y-14=0 y³-8+y²-4+y-2=0 (y-2)(y²+2y+4)+(y-2)(y+2)+1(y-2)=0 (y-2)(y²+3y+7)=0 y²+3y+7=0 ∆=b²-4ac ∆=3²-4•1•7 ∆=-19<0 reject y-2=0 y=2 7^x=2 x=log_7(2) ❤

I mean what is wrong if we took matual 7 to the power x and its 1+1²+1³=14 It's not working but i want to know why can you explain plz

Thanks for the video. You are touching on a very tricky topic. The definition of the log of a complex number leads to some contradictions which need exclusion and specific treatment. To say it differently I would not touch this animal :-). By the way I think that dividing the polynomial by t-2 (knowing that 2 is "evident" solution) and solving the quadratic equation is a shorter path. Good job anyway.

Good work my fellow Mathematician ❤ keep up with the content I have subscribed

❤❤❤ Спасибо, что развлекли на полчаса. Молодость вспомнил (мне уже 67 лет). Все зависит от области допустимых значений, (как меня учили когда-то в школе), которая здесь, увы, не оговорена. Без этого игра с числами не имеет смысла. Поэтому область этих самых допустимых значений установил себе сам: 1.Если это просто школьный прикол, то ответ простой: "-1". Для такого "решения" понадобилось ~30сек На областной олимпиаде по математике была задача о рыбах, где ответ был такой же, только числа в ответе отличались 2.Если это реальная задача с областью допустимых значений, где x больше 0, то: x ~ 1,6640625, если преобразовать это уравнение так: (x•x - 2)(x•x + 2) = x + 2; x•x•x•x + 2•x•x - 2•x•x - 2•2 = x + 2; x•x•x•x - 4 = х + 2; x•x•x•x - x = 4 + 2; x (x•x•x - 1) = 6 (эти преобразования на уровне средней школы тогдашнего моего выпуска ). Комп не работает, есть в доме только бухгалтерский CASIO (DM-1200) с 12-тью цифрами на экране. Мое наследство от умершей от COVID жены. Я чудом тогда выжил. Но это так, к слову... Имеем только этот арифмометр и то "преобразование", на котором проще его вычислять (в практической области допустимых значений, где x больше нуля), т.е. : x(x•x•x - 1) = 6 При x =1: 0 не равно 6; При x = 2: 30 не равно 6; Принимаем значение x, равное половине этого интервала, т.е. : x = 1,5 , при котором 3,5625 не равно 6; Принимаем значение x, равное половине этого интервала, т.е. "+", например, к его нижнему значению, где x = 1,75 , при котором тоже 7,62890625 не равно правой части уравнения, т.е. 6; Принимаем значение x, равное еще половине интервала, но уже на понижение, где х = 1,625 , при котором 5,34790039062 не равно 6; и т.д. , половиня интервалы куда надо. Вот так я и получил на простом бухгалтерском арифмометре x = 1,6640625 когда уже было: 6,00387448441 которое было все еще больше тех 6. Можно было бы это продолжать и далее, пока CASIO не выдал бы 6,000...000 в силу своих возможностей, "округлив" очередной результат этих вот вычислений, т.е. как и заложено было в его программе (возможностях его) изначально его творцами. Кстати: допустимая погрешность вычислений - это совсем уж отдельная тема!!! Эти все подробности излагал не для Вас, взрослые, а для школьников: а вдруг математика кому-то из них понравится??? P.S. А Вам, для прикола, вот эта школьная задачка, из тех лет: Три товарища пришли в ресторан "гульнуть". Каждый дал официанту по 10-ке. Уходя, попросили рассчитаться с ними. Тот, зная что они "гульнули" на 25-ть, украл с этой суммы себе 3-и и сообщил им, что "нагуляли" они по 9-ть с каждого, вернув каждому из них по 1-му. Т.Е.: по факту они заплатили 9 х 3 = 27, а 3-и он себе прикарманил. 27 (9х3) они оплатили по факту + 3 (он себе "прикарманил") = 29!!! Куда делся 1 рубль, доллар или евро из тех 30-ти ??? С уважением к Вам, Василий

x^2=t t^4-t=9(t^2-t) t^4-9t^2+8t=0 t^3-9t+8=0 (t-1)(t^2+t-8)=0 t=1(no),t^2+t-8=0

This is a very simple math problem and not a Math Olympiad Problem.

I did this in my head in less than a minute, using the obvious method illustrated by @key_board_x below. I don't understand the point of this video.

Much better to change variable and solve, let Z=x-5 and solve. You obtain a linear equation of square root of Z.

Bro k⁶=64 =⁶√k⁶=⁶√64 =K=2

Squaring when solving, or indeed cubing etc, can introduce fallacious solutions. It’s vital to point this out before starting, very clearly, that all solutions should be checked. An explanation why this occurs would be useful to enquiring minds. Before starting, it’s often a good idea to sketch the functions graphically.

Cube root of 4/9? If you want a numeric value beyond that, use a calculator.

For the problem given, without conditions for k, which in theory is a constant, variables use w,x,y,z, k=-1,3 If you require complex solutions, you should state this in the initial conditions. Then a simple application of (cosθ+isinθ)^n=cosnθ+isinnθ, gives the necessary solutions. 5 min would be lengthy.

Навіщо так складно? 🤔 Двічі підносити до квадрату, щоб потім відхиляти лишній корінь рівняння; ділити на 2, щоб потім множити на 4; виносити за дужки 4, щоб скоротити дріб на 2 і лишитися з виразом із двійкою за дужками? 🤷🏻‍♂️

2(a²+b²)=(a+b)²+(a-b)²=62 So, X= 2 Easy

Я тоже так решила

More simple: (x/2)^6=3^6, (x*1/2)^6=(1/2)^6 * (x)^6 (x)^6=[3^6/(1/2)^6] (x)^6=[3^6 * 2^6]= (3*2)^6 x1,2=+-6.

I Haven a different solution. Can You check plecase if my solution is corect? 15=16-1, 15=4^2-4^0, 4^(x-2)=15 =» 4^x/4^2=4^2-4^0 » (2^x)^2=240 (2^x)=4✓15 x=log(4✓15), base 2 of log.

The hell is this video... delete it please

Educate us by explaining the reasoning behind multiplying the numerator and denominator by the nth root of a to the n-1, please.

The author created a lot of unnecessary entities. Everything is solved much easier if the variables and constants are immediately separated.

Simplify by X^2, then by x^2-1 : ok, but you have immediately précise, thé solution (s) MUST bé différent from , respectively : 0, +1, -1 (even if it IS quasi évident....)