【検証】東大医学部は本当に数学できるのか?【ドッキリ】
Вставка
- Опубліковано 7 лют 2025
- 東大医学部の頭の中、全て見せます。
初見で解くと、思考回路がわかるよね。
(by DD兄弟)
P.S. 今日のパスチャレの答えはこちら
note.com/pfsbr...
~~~~~~~~
■東大医学部発「朝10分」の受験勉強cafe
PASSLABOのチャンネル登録
→ / @passlabo
■東大生たちと一緒に勉強したい方必見!
公式LINE@登録はコチラから
→ line.me/R/ti/p/...
(勉強法や質問相談はLINE LIVEにて配信予定!!)
======
【君のコメントが、動画に反映されるかも!】
問題の解説希望やリクエストあれば、好きなだけ載せてください。
1つ1つチェックして、役立つものは動画にしていきますね^ ^
======
■偏差値43から東大合格までの勉強法がまとめて知りたい方
→ amzn.to/2GRW3tL
■公式Twitterはコチラ
→ / todai_igakubu
===========
■PASSLABOメンバー情報(note)
*気になるメンバーのnoteをチェック!!
「1」宇佐見すばる
東大医学部 / PASSLABO室長
→ note.mu/pfsbr1...
「2」くぁない
早稲田 / PASSLABO切り込み隊長
→ note.mu/pfsbr1...
「3」あいだまん
東大逆転合格/ PASSLABO歌のお兄さん
→ note.mu/pfsbr1...
「4」くまたん
東大文一1点落ち?/PASSLABO癒しキャラ
→ note.mu/pfsbr1...
===========
#PASSLABO
#東大医学部発
#概要欄も見てね♪
朝6時半にほぼ毎日投稿!
一緒に動画で朝活しよう





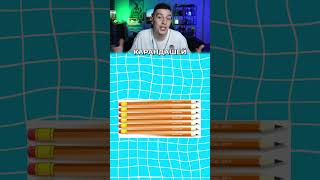



相加相乗平均、判別式、解と係数の関係、文字で置く、範囲を考える………この問題1つでめっちゃ大事な数学の要素を考えれる、めっちゃお得な問題やな。
それな^_^
最近 塾講師を始めたのものです。
改めてスバルさんの考えの深さを
思い知ります。尊敬します
この解法だと「なぜ分母分子をx^2で割ろうと思ったか?」のところをもっと深掘りして解説しないと、一歩目でつまづく。ここを「思いつかないとアウト」にしちゃうともったいない。
分数関数の基本はまず「(分子の次数)≧(分母の次数)のときは割り算して字数下げ」なので、まずは与えられた分数式をx+1/(x^3+x)に変形する。さらに1/(x^3+x)=a/x+(bx+c)/(x^2+1)と部分分数分解を考えてa=1,b=-1,c=0を得る。ここまでやれば、x+1/x=tとおく方針が見えやすくなります。
凄い分かりやすい、、、
やっぱり色んな方法を考えてみるのって大事ですね、、、
ほんとに笑っちゃうくらいわかりやすいしどんな場面でも使える大事なポイント押さえられてるからすごいですよ。ほんとに。
数学の解法で
自分が笑ったのは
何十年ぶりです(^◇^)
いろいろな解き方で解く・・・正に数学力アップの王道のような気がしました。
1年前はこれムズっ! って思ってたけど 今見たら普通に解けるようになってました
うれしい
冒頭「自粛中数学解いてなくて鈍ってるんじゃない??」
私((青チャート耐久してたやん……めっちゃ数学解いてるやん……))
多分この人たち青ちゃは数学じゃないとか言い出すんだよ(震え)
パスラボ見てたら、出てくる人が好きになった
こういう頭いい人の数学の解説見てるとだいたいみんな問題をパターン化して解きやすくしてるよな。
ある程度暗記は必要なんかな
スバルさんが問題集を解いてる間、あしだまんとくまたんが筋トレ耐久して、ぷろたんみたいになる企画お願いします!
②の考え方って逆手流(逆像法)
ですよね!
最大最小問題とか軌跡、通過領域の問題で効果抜群👍
塾の先生が、微分して答え出す前にこの動画みたいにグラフ書いてみるとある程度あたりをつけられるって言ってたなー
グラフ使った解答は厳密な記述が難しくなるから、どっちにしろ微分する羽目になるぞ
代数的に解くならいいけどね
志築智己 もしかして広瀬先生ですか?
最近話題になっていた相加・相乗平均の最小値についても触れられていてさすがです…!
問題見た瞬間2パターンって言えるのスゴいなぁ。
複数解法が浮かぶように頑張ろ
x=1で最小取るなぁと直感的に分かったが、論理的に説明できなかったので動画見終わった時の納得感半端ない。
言語化された後だと、直感的に単調増加だってことに気づいたんだなぁと思った。
5年ぶりに見たけどわかりやすすぎ😂
もっと早く動画出して欲しかったな😭
相加相乗平均しようとして解けなかった…
ガチガチ…
高1だけど楽しく見れる!
最高です!
y=x+1/xとおくとy-1/yの最小値を求める問題に変換できる。y>=2(x=1)なので求める最小値は3/2
いつも楽しく見て来ます(リズムが大好きです)。シェアさせてください↓↓↓二番目の解法、いつもやっています。グラフによる視覚化は大切ですね。
おはようございます。すばるさんすごい😅Dッキリにも動じてない。楽しい動画をありがとうございます😊
解法もとても美しい物でしたが、それ以上にすばるさんの普段から解法を体系立てて整理している様子が垣間見れました。これからは、ある程度統一されたアプローチが出来るように、解法をうまく整理していきたいです!
(x+1/x)-(x+1/x)^-1
と変形して二つの項で相加相乗を使って
(x+1/x)-(x+1/x)^-1≧2-1/2=3/2
ど、どゆことですか??👀
相加相乗ってx>0,y>0じゃないと使えないんじゃ…
hr m 両方正なのであってますよー
@@しょーごしょーご-d5h
動画のようにx+1/x=tとおくと、t≧2がいえて(等号はx=1のとき成立)、逆数をとると、
0 < 1/t ≦ 1/2
となり、-1をかけると、
- 1/2 ≦ - 1/t (< 0)
が得られます(等号成立:x=1)
これとt≧2を合わせて、
t - 1/t ≧ 2 - 1/2 = 3/2
運慶 自分もそうしました
こんな風に解きました。
x^4+x^2+1/x^3+x 因数分解すると
(x^2+x+1)(x^2-x+1)/x(x^2+1)
x^2+1=tとおく
(t+x)(t-x)/tx = t^2-x^2/tx
2乗する(元の式もtもxも正なのでok)
x^4+t^4-2t^2*x^2/t^2*x^2 = t^2/x^2+x^2/t^2-2
ここでt/xの取りうる値について考える。
全体をkと置いて判別式からt/x>=2
よってt^2/x^2>=4
t^2/x^2=pとおいて
p+1/pについて考える。
相加相乗平均よりp>=4なので最小は17/4。
(17/4)-2の平方根より3/2。
この人あれよな。数学の本質押さえてるよな。
それがわかるってことはあなたも
数学って楽しいんだな
久しぶりに教えてくれたとてもいい動画
さすが理3ですね(^_^)
本質って言葉使った途端
薄っぺらい人間に見えるのは私だけでしょうか
ですたなか だけではないがひねくれてると思うよ
れじいみらあ31 理科二類から医学部なんですよ
すんっっごいためになりました!
受験控えてるのに知らない公式というか解き方というか定義というのかいろいろ出てきて焦りが出てきました…
ソーシャルディスタンスは、タイムリーな感じでおもろかった
朝の少しぼーっとしてる脳を起こす時にすごく良い問題でありがたい
おはようございます。
意外とDが多くて笑いました。
行ってきます。
分子をx^2(x^2+1)+1 にして
分母もx(x^2+1) になるから
微分で割と綺麗になる。
x^2=t(>0)←これまじ大事
とかで置いてあげると楽になる。あとは増減表書いて終了。
何をtと置くかとか、分子をどうやってtで表すか辺りが個人的に鬼門。
演習量なんだろうな〜
そうはんほうていしき
文系数学の相加相乗使う率結構高いですよね
僕も相加相乗平均の関係使おうかなと思いました。
理系なんですけどもね
クローバーぁ 僕も理系なのですが、すぐ微分、に走る人よりサラーっと相加相乗という考えが出てくる人は賢い、という印象があります。0より大きいという確認なしで使うのはその限りではないですが。
この手の問題は、自分ならまず間違いなく最初に微分しちゃいますねw。置き換えて単調性を利用する解き方だと、計算量が激減して、計算ミスのリスクも減りますね。(勿論、与式を微分しないと解けない問題も多数ありますが。)
こういうスタイルの動画を待っていた
珍しく方針自力で考え付いて嬉しかった
感動😭数学好きになりました!
ずっと思ってるんだけど
t=x+(1/x)っておいてtの変域出すとき、相加相乗と等号成立でt>=2って言ってるけど、これは不十分。lim(x→∞)とかを考えてtが上に有界でないこと、かつx+(1/x)が至るところ連続であること、の2点を言わないとtが2以上のすべての実数をとることは言えない。
チャート式もずっとこの間違いを犯していてそれを放置している。
解決法としては、相加相乗平均ではなく、しっかりとxの二次方程式の実数解条件に持ち込んでtの範囲を出すこと。
パスラボさんにはこれにしっかり触れて受験生に広めてほしい。模試では引かれないかもだけど難関大入試本番では確実にこれで1点は引かれてしまう。
このコメント欄を見ても
疑問が残る方に
補足させていただくと
4分の式の両辺をx倍しその方程式の解が正の解を持つ条件として
軸と端点の条件を用いて求めると
というものだった気がします。(間違いがあれば気づいた方訂正よろしくお願いします)
6:06 tはt-(1/t)=kという分数式の分母だからt≠0が前提となるのでは?その辺どうなんでしょ?
tは2以上だから
@@piman_taro そう、t≧2(かつt≠0)だからt=0 でf(0)=・・と考えること自体ナンセンスでは‥と言いたいわけです。愚問だったらすみません。
@@dqr7336 え?マジですか?すみません、自分は数学が出来ない部類なもので‥ t-1/t=k から①に式変形する際に「ただしt≠0」としなければならないはずで、その次にf(0)=~と論ずるのは?と抵抗感がある訳です。式変形は制約が伴うのが鉄則と学んだ世代ですので‥間違ってたらすみません。
tora toratora
すいません、上の僕の説明は完全に間違えているので忘れてください
当然ですが、今はt-1/tのt≧2における最小値を求めようとしています
ここで、t-1/t=kとおけば「t-1/t=kかつt≧2」…②という条件のもとで、kの最小値を求めればよいということになります
しかし、この条件式はわかりにくいのでわかりやすいものを考えます(動画の最後の解法ではk→yとしてy=t-1/tのグラフを考えて、この条件から直接求めていますね)
②は、意味することが変わらないように変形することができて、②⇔「t^2-kt-1=0…①かつt≧2」となります
(t≧2なので条件式に勝手にtをかけても良く、①とt≧2という式は別々に扱っても良いということです)
この条件を使ってkの最小値を求めます
ここで、f(t)=t^2-kt-1とします
f(t)=0…①
①の解の配置を調べるために、y=f(t)としてグラフの形を考えます
y=f(t)のグラフそのものにはt≧2という制限はないので、f(0)を考えればグラフの概形がわかります(点線で描かれる部分を考えているということです)
よってグラフの概形がわかり、①が正の解をただ一つ持つことがわかったので、
①がt≧2の範囲に解を持つ、(⇔放物線y=f(t)とt軸がt≧2の範囲に共有点を持つ) ようなkの範囲を求め、そこから最小値を求めたということです
間違った説明で混乱を与え、余分な時間を使わせてしまい申し訳ありません
(tの関数のグラフを考えるならtでかけたり割ったりすると当然グラフの形は変わります、私の勘違いです。)
高校数学に対する理解が深いと、他の道具と照らし合わせながら全体を俯瞰して問題を解くことができるということがわかりました。
公式とその公式が成り立つ理由を知る→基本問題を解く(公式の理解ができているか、その理解が正しいかを確かめるため)→演習問題を解く(問題文から使うべき公式を導き出す力をつける)→応用問題を解く(全ての公式を網羅しているか)という形で勉強するべきなのかなー
公式が存在しないこと、例えば会社経営だと、①メリットとリスクをある程度把握する→②とりあえずやってみる(言葉では表せないような感情や細かい出来事を知る)→③経営しながらトライアンドエラーを繰り返す
って大まかに言えるかも
おはようございますー!!
おはようございます!DD兄弟笑
PASSLABOと鈴木貫太郎先生の動画見始めてからマジで数学楽しくなってきて草
数学の難問解いてる時がめっちゃワクワクする
武者震い的な
これは式の形から解答の道順が分かりやすいですね。
解けそうで解けない
パスラボさん……難しい……でも観たらわかったからOKですね!(納得)
本当にわかりやすいです!!!
2, 3分で解けましたが、これ、面白い!
まさかの微分禁止でしたか。一気に難易度が上がりますね。これまた勉強になりました。
x^2で割るという発想がなかった。
なぜx^2という文字で割っていいのでょうか?
頭が悪いので教えてくれると嬉しいです
ごめんなさい
解決できました
最初にx>0って書いてありましたね
DD兄弟面白いですね!!
Dっきり、ぱんD、D画とかの言い方がQuizKnock の企画であるDDDDDを思い出します!!
伊沢さんが結構こだわって言っていました!!
この問題を初見では解けませんでした・・・
すばるさんさすがです!!
オープニング面白かったです笑
Dのネタまあまあ面白かった笑
判別式が出てくると思ってました。
あ、なんかすいません
なんかこの時間に目が覚める
汝?
@@瓦林遼太郎 誤字
y=t-(1/t)ってグラフはy=tが漸近線だから…って書いてもいいのね!
問題のパターンに応じてどういう方針が良いかなどをまとめた動画が欲しいです!!!!
俺は微積に支配されてる気がします
皆さん。ここでのパンダちゃんの「レベルが低い」は褒め言葉なので暖かい目で見守りましょう。
@@aimy0306 どうしたん??落ちたん????
おはようございます!前半2人ともめっちゃ可愛い爆笑
受験終わって久しぶりに見にきたけど、やっぱり楽しいなー
手軽に見れる
単純に与式をx+1/{x^2(x^2+1)}と変形して微分し、(x-1)(x^5+x^4+3x^3+3x^2+x+1)/{x^2(x^2+1)}^2となってx=1で最小と解きましたね...x^2で割れば綺麗になりそうという発想がパッと出てこない()
解と係数の関係は中学生でも知ってる人はいるかも。塾技っていう高校受験用参考書に載ってありましたし。
⚠️オープニングの2人は東大生です
くまたんは違うんですけれどもね
あいだまんさんの髪型、可愛い感じですね笑笑
くまたんゴツいて
文系のくせに一日2時間は数学やってるww
二次で数学使うからってのもあるけど楽しいからでもある!!
意外と文系でも数学が合否を分けますからね、お互いがんばりましょう!
文系で数学出来るぞ!ってなったらリードできるぞ!頑張って!~
数学って絶対立ち止まる時ってあるんだけどそれを理解して自分で解けるようになる時の快感がどの教科よりもやばい
@@ajmmgtj
脳「美味しかった」
普通に理解してるジャン。強
相加・相乗平均でt≧2と出て、なおかつ等号成立を確かめたとしてもtは2以外の数をとるか確かめてないので、もし答えでtが2以外の数の時最小であればそのtをとるxを考えないといけないですか?
今日も面白かったです!
相加・相乗平均では範囲だしても減点だよね
理系の人は相加・相乗平均で範囲だした後に、何か増加関数なんちゃらかんちゃら書いて議論完成させるらしいから使ってもいいんだけど
文系の人はそれ習わないから、ちゃんと分母払ってXの2次式にしてX>0の範囲に解を持つ条件でやってね
答えは一緒になるから
式を羅列するのもいいけど、グラフで視覚的に解く
っていうのも面白いね。
動画今から見ます。文系の自分はまず分子の次数下げか、分子と分母を割って相加平均使うことを考えた。前者の場合だと次何すれば良いか分からなかった。
後者の場合だとx二乗で分母分子割ると対称式出てきて、分母をtとしてtの式にできた。このとき分母は文字で置いたからtは2以上。あとは分子因数分解できて増減表書いてtが2のとき最小値3/2をとった。理系だったら微分で一瞬なんだろうな、
動画サラッと見たけど、途中までの方針は一緒でうさみさんだと次数下げして存在範囲に着目したをみたい。因数分解できなかったら次数下げして存在範囲で解くと思う。この問題みたいに、分数式で因数分解できるなら、各項の正負に着目して増減表書くと最大最小わかるのでおすすめ!
ちなみに河野玄斗の相加平均についての動画は、分数式の解説も乗ってるからおすすめ
いい問題やな〜
(与式)=x+(1/x)-(x^2/x^3+x) 相加相乗平均より x+(1/x)
諦めて微分しましたが、解けました!解と係数との関係で解くやり方も身につけます!
6:34あたりからよくわからないです。f(2)が0以下なのは何故ですか?
自分もきになります
t>=2…①を変形すると-1/t >= -1/2…②が出るので、グラフを描かなくても①+②でt-1/t >= 3/2 が出ますね(*´▽`*)
5:15 実数解を1つ以上持たないといけない理由が何度見直しても分からない
求めたい値を文字で置いて、勝手に作った方程式なのに、何故実数解がないといけないんだ・・・
そもそもやけど、なんで分母分子をx^2で割ろうと思うんだ?
なんか綺麗になりそうっていう感覚なんかなぁ?
kが存在するということはそれを満たすtが少なくとも1つはあるということからですね。
x^2で割るのは無理やりでも約分して次数を減らしたいからです!
これ見た瞬間いきなり微分したくないわなw
さすがすばるさん。
ぜひ河野玄斗とコラボしてほしい
確かに・・・!
やめてほしい正直
与式を x+1/(x^3+x) と変形した上で、x>1 でも x
文系だけど相加・相乗平均より=k出おく方がいいなって思った
相加・相乗平均もっと勉強して使えるようにしなきゃ😥
解の配置問題に置換できる人頭柔らかいな
T兄弟面白かった
tが実数だから判別式がd≧0ではないのですか?
なぜd>0なのですか?
引き出しの多さといい喋りといいほんと凄いな
以前、センター数学の追試を不意打ちで解かせてたのを思い出しました笑
最後の解法が相加平均相乗平均が出来ている理屈で草
初見で教えれるんだなぁ、さすがで
相加相乗で範囲示すのはあかんやろ
Dずっと使ってくれ笑笑
最初にx^2で割るって言うのはただの閃き?それともこうゆう問題では典型なんでしょうか
もし xが2^xとなったときの 問題を
解いてほしいです!
登録者の伸びが凄い
忘れた頃にやってくる 偶数にして👍
はく いいね稼ぎのくせに3週間経っても19いいねしかないの草
@@yukimy_R そっからご時間経ってもひとつも増えてないの草
3年経って30😊
偶数でよかったね
いいね稼ぎしても現実は良くならない事実をしれてよかったね😊
今から学校行ってきまーす笑
x+1/xをノータイムでtとは置けない、、、
凄いっす、、、
講義内容も素晴らしいが、前座(?)も面白い。
(x⁴+x²+1)/(x³+x)=x+1/x-1/(x+1/x)
相加・相乗平均 x+1/x≧2
∴ (与式)=2-1/2=3/2
いちばんはやいと思う(自己満)
あいだまんからの企画最高
これ微分したらめんどいし計算ミスするかもしれないから試験で出ても微分で解かない方がいい。