sin derivative of cos
Вставка
- Опубліковано 7 вер 2024
- In this video, as a follow-up to my exponential derivative video, I calculate the sin-th derivative of cos, using the power series of sin. The answer is very strange, as you'll soon see! As you can see, this technique applies to any function which has a power series, so this example is just a special case of the general technique. Enjoy!
Note: Link to the exponential derivative video: • Exponential derivative


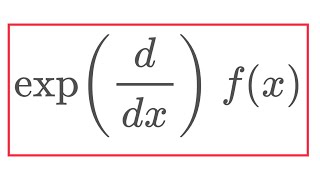





Won't somebody stop this madman!
Next video: "The derivativeth-derivative of e^(-x^2)"
Kiritsu Hahaha that’d be awesome!!
@@angelmendez-rivera351 dude sin derivative has no meaning either before this crazy youtuber give meaning to it
@@williamnathanael412 To be fair, he did exp(d/dx) just for fun, and that has applications in quantum mechanics.
@@williamnathanael412 Oh you just wait, I bet someday some crazy physiscist will find a way to use this sort of shenanigans xD
Next zeta functionth derivative of gamma function pleeease.
Can they be expressed as power series?
They can:
fractional-calculus.com/series_expansion_gamma_reciprocal.pdf
math.stackexchange.com/questions/2618488/taylor-series-of-gamma-function
math.stackexchange.com/questions/2029777/on-the-maclaurin-expansion-of-the-riemann-zeta-function-and-a-related-sequence
However, the coefficients are 'ridiculously hard to compute' [second link].
This series in a few years will be like:
Solve the differential equation
sin(D)y+exp(D)y+arctan(D)y+xy'=0
A few years? Haha
@@drpeyam I don't know how many new derivative operators you are planning to construct :p
Also I have been tinkering around with a "binomial derivative" B(n)=(1+D)^n this morning. It's quite interesting because it allows to solve homogeneous differential equations B(n)y=0 (it is trivial to solve for n≤2 because they are second order n>2 is probably solvable too but I don't have the skill set to do so)
I also worked through binomial derivatives of some well known functions (assuming they are correct):
•B(n)e^x = 2^n e^x = exp(x-n ln2)
•B(n)sinx = 2^n-1 (sinx+cosx)
•B(n)(ax²+bx+c) = ax²+(b+2na)x+(c+n(n-1)a)
The last one implies that one can easily solve the following differential equation for any n:
B(n)y - y = kx + h
To be
y= (k/2n)x² + (h/n - k(n-1)/2n)x + C
Likewise the following are also solvable for all n:
B(n)y - 2^n y = 0
B(n)y - 2^(n-1) (y + y') = 0
using the other functions
Whoa, this is freaking awesome!!!! I might actually turn this into a video someday, thank you!
@@atrumluminarium I know, this was more than a year ago, but you, sir, just blew my fucking mind. :O
@@atrumluminarium have you played around with negative, fractional, or complex values of n for the binomial derivative? As I understand it, this extension is understood with true binomials and perhaps you could find some interesting results. Veritasium's video about Newton's approximation of pi touches upon it which is why it occurs to me.
There is no stopping this mad man.
These kind of objects are actually used in quantum mechanics. For example, e^(-2pi*i/h*p*a) is on operator which shifts the wave function of the system in space, expressed by the momentum of the syste.. p, the momentum operator is h/2pii*grad. Ultimately this is connected to continuous symmetries being expressed vy lie groups, and the elements of the lie algebra being the operators of conserved quantities.
This idea is very clever. However, before I saw your videos about exponential derivative, I had thought that it is generalization to fractional derivative. Since I had seen your thumbnail, I thought it should be written as ((d^(e^x))/(dx^(e^x))) f(x) and calculated like fractional derivative. For example, like D^(e-2) (f'' (1)) (where D stands for fractional derivative). Although this isn't what I expected, I find your videos about differential operators very interesting. And I know that my idea might not be even possible to calculate.
Hmmm, I feel as though saying this is the ‘sin’th derivative is wrong because we don't have D^sin(x) instead we have sin(D). The notation in the thumbnail is misleading in this sense. Now that I think about it, D^f(x) sounds really interesting and could be a good video idea.
I think sin(D) makes more sense.
Wow I never thought of that, unfortunately ln(x) has a pole at zero so power series won't work and also it is branched in the complex plane and since this stuff tends to work with complex numbers introducing ln(x) may stop things being unique. If we have x as a rational then D^x becomes D^a/b so we are asking for an operator that when done 'b' times gives us D done 'a' times. This is then extended to all reals and can be defined explicitly, search fractional derivatives if you want to see how people make sense of D^x for all reals (Dr Peyam has vids on this).
You are probably familiar with all this if you know operator calculus, sorry if this is trivial for you.
@@angelmendez-rivera351 , maybe we can find ln(D) by solving e^F=D where F is some operator, expanding with power series seems like a good first step but I have no idea how to go further.
Yeah I know, but the thumbnail looks nicer that way!
@@angelmendez-rivera351 That would make sense for d/dx^(e^x) for x
Hey, Peyam! This was a great video! One thing I noticed was:
sinD(sin x)=D(sin x)*sinh(1) and
sinD(cosx)=D(cosx)*sinh(1), where
D(sin x) and D(cos x) are the regular derivatives of sin x and cos x, respectively. And I thought that was pretty cool and interesting!
I never knew I needed to know this, but boy I love it!
next: arithmetic differential equations lol
Next Xth derivative of X
The x-th derivative of a function is just the ordinary derivative 😉 At least based on the definition of the f th derivative
i mean, the xth derivative at x=5 would be the fifth derivative of y, and so on. for example, x^5 you see a graph that (kinda smoothly?) follows the points (0,0), (1,5), (2,160), (3,540), (4,480), (5,120), (6,0) (n>6,0)
Next do ζ(D) and determine the eigenspaces and eigenvalues of it.
Then also maybe Γ(D).
The more natural way to write the derivative is to note that it be the imaginary part of exp(id/dx)f(x) = f(x+i) and the cos derivative will be the real part.
Dr Peyam, i think you could use the exponential derivative exp(D)f(x)=f(x+1) to redefine the cosine and the sine derivative as cos(D)f(x):= (f(x+i)+f(x-i))/2 and sin(D)f(x):= (f(x+i)-f(x-i))/2i, it gives the same results above in your video
So, does that mean that exp(kD)f(x)=f(x+k)? And then you can linearly combine them, so exp(kD)f(x)+exp(mD)f(x)=f(x+k)+f(x+m)?
k,m ∈ ℂ
Yes, this is even true in higher dimensions with f(x +a) = exp(a 'dot' nabla)f(x).
What if f is not defined for complex numbers
Hey, Peyam! One thing I noticed was that taking the sin derivatives of sine and cosine multiplied their respective regular derivatives by sinh(1), which made it very easy for me to remember. And I thought it was pretty cool!
Hi Dr Peyam. I don't know if anyone else has commented this yet but I think I have figured out how to simply express sine and cosine derivatives of functions f(x). The sine derivative of f(x) = (f(x+i)- f(x-i))/2i, whilst the cosine derivative of f(x) = (f(x+i)+ f(x-i))/2. Also, the sinh derivative of f(x) = (f(x+1)- f(x-1))/2 whilst the cosh derivative of f(x) = (f(x+1)+ f(x-1))/2. The exponential derivative of f(x) indeed equals the sum of the cosh derivative of f(x) and the sinh derivative of f(x). The sine and cosine derivative formulae look very similar to the Euler formulae for sine and cosine, where the top of the fraction is a combination of ith and -ith exponential derivatives. You can also easily prove that the sinh and cosh derivative formulae hold for x^m.
These derivative functions applied to x^m are also really neat. Exponential derivative of x^m = mC0(x^m) + mC1(x^m-1) + mC2 (x^m-2)+ mC3 (x^m-3) + ... The sinh derivative of x^m = mC1(x^m-1) + mC3 (x^m-3) + mC5 (x^m-5) +.... The sine derivative of x^m = mC1 (x^m-1) - mC3 (x^m-3) + mC5 (x^m-5) - mC7 (x^m-7) +.... The cosh derivative of x^m = mC0 (x^m) + mC2 (x^m-2) + mC4 (x^m-4) + ..... The cosine derivative of x^m = mC0 (x^m) - mC2 (x^m-2) + mC4 (x^m-4) - mC6 (x^m-6) + ...... For example, the sine derivative of x^9 = 9C1(x^8) - 9C3 (x^6) + 9C5 (x^4) - 9C7 (x^2) + 9C9 = 9x^8 - 84x^6 + 126 x^4 -36 x^2 + 1. It'd be really cool to see you cover this in a future video (I don't think you've made one on this yet).
There might be confusion around the notation sin(D)x. sin(D) is not sin of D, it’s more like another function based on sin(x).
Could you talk about dual numbers? Since the topic is unusual ways to take derivatives, I feel that it would be relevant.
Interesting! I’ll look into that!
Love you channel! Thanks for sharing the stuff! %-)
The math gets more fun with your vídeos
Awesome!! (As always)
If you do exponential series but with the integral operator you get the shifting but with -1, which is kinda expected but still really cool.
Hey! I've been messing w/ similar ideas in my freetime using residue; not to sound presumptuous, but can you find a closed form for e^(ad^n/dx^n)f(x)?
- sin(1)*sin(x) is equal to (cos(x + 1) - cos(x - 1))/2 via Werner's formulas.
DeaR Peyami Bro Best regard from Turkey
U'r legend 😍❤
I found a general form for sin(D)
Notice that
exp(D)f(x) = f(x+1)
exp(nD)f(x) = f(x+n)
exp(iD)f(x) = f(x+i)
Since sin(t) = Im[exp(it)]
Re[exp(iD)f(x)] = Im[f(x+i)]
So...
sin(D)f(x) = Im[f(x+i)] , and
cos(D)f(x) = Re[f(x+i)]
Using Leibniz notation, you might write
g(d) f(x) / g(dx)
for the function-derivative by g of f with respect to x.
This makes linear differential equations feel truly linear. You can say
g(y) = y^2 + 1,
g(d) f(x) / g(dx) = 0,
which gives that f(x) = sin(x) {not 0-function, yadda yadda}. A trivial example, but a nifty one.
Also, g(e^x) = g(d) (e^x) / g(dx). It just pops right out.
g(d) (e^u) / g(dx) for any u(x) is a tougher problem, but not really.
An interesting challenge would be using a parameter function g_n(y), then asking for a function derivative by g of f(x) in terms of x and n.
I want to see what this kind of idea would mean if we wanted to talk about Fourier transforms instead of Maclaurin Series.
Beautiful, thank you!
I wonder if you could prove that this definition would hold on branch cuts if the functions in the differential operator weren't entire.
Enjoyed it as always! Hmm, I've never seen any antiderivative versions. Something to explore? By the way, in vector calculus, you skipped showing that the integral definition of divergence (given here: en.wikipedia.org/wiki/Divergence) is equivalent to the differential version. The divergence theorem plays an obvious central role in proving this result. If you mentioned it already, and I missed it, then I apologize XD. But I think it would make for a nice video on its own. It would also give you a chance to show off your skills in (mathematical) analysis. ;)
I hope this video wasn't as glitchy for everyone else as it was for me.
Make the inverse (Sine integral)
I don't think this would be possible, this derivative amounts to taking the imaginary part of f(x+i) which is an operation that is non invertable.
@@camerontorrance1992 i know I’m two years late, but this was just one way to do it. You don’t need complex analysis.
@@cpotisch Ok but expressing it this way makes it quite clear that this operation discards a lot more information about the original function than the normal derivative does, so you aren't going to get a pleasant theory of anti-sin-derivatives.
@@camerontorrance1992 Sorry, but you're still wrong. Just did the math and the sin-th integral of cos is sin(x)sinh(1).
@@camerontorrance1992 How did you conclude that it's "quite clear that this operation discards" information?
That's odd cause if you divide the last 2 equations then you get: cot(x)=-tan(x) but it should be: arccot(x)=-arctan(x)??
Last time you said that it might be useful for the lie groups. In the last year I've been very reading about quaternions and dual quaternions. what where you tinking about the usefulness of this derivatives in the lie groups?
Okay, there’re some cool suggestions in the comments but an exciting one is missed. Bow down before the imaginary derivative of f(x) :D
9:45 THE MEANING OF IT ALL!
I have a general formula for the sin derivative, sin(D)f(x)=(f(x+i)-f(x-i))/2 for any function admiting a Taylor serie.
That’s ok if you’re ok with complex functions, also there should be a 2i on the denominator
That's right I forgot
For ln function, the i disapears
On the numerator at least
So, sin(D)(x)= i !!! .
What about the Gamma function of D?
You should do the sine of a fractional derivative next
Is there any other way to go about this type of differentiation if the function is not analytic?
What is the "overall name" for these g(x)-th derivatives of f(x) so that I could look it up on Wikipedia or sth?
@@angelmendez-rivera351
Oh okay🤔 Thx a lot
Just asking for confirmation, so what Dr. Peyam has done in this video is that "operator calculus" stuff?
I kinda made this concept up, there’s no name for it
@@angelmendez-rivera351
Yes, I did found it on Wikipedia.
So, Dr. Peyam, there IS a name for what you have done in these videos.
The previous video about e^x-th derivative of f(x) is literally the "Shift Operator" introduced by Lagrange.
Anyway, this video is still awesome so I could have one more thing to study before sleeping lol
Well yes, I know the shift operator is the shift operator, but I haven’t found a name for the f th derivative of g :)
8:18 why it's linear ???
Are there cases where the sum diverges into infinity? Can those be represented algebraically?
Definitely! I’m thinking of cases like the ln(x+1), derivative of f, which depends on the radius of convergence of ln(x+1)
@@angelmendez-rivera351 in functional analisis you can do this pretty easily. Physicists use this all the time (most of them very not rigorously).
@@angelmendez-rivera351 I honestly tought spectral theory is considered part of functional analysis, my bad. Actually I still think so.
Is there something like a half integral or something like that?
Yep, the -1/2 th derivative!
Why is such derivative useful? Is it a mathematical trick or is there an application worth mentioning?
In quantum mechanics, you use thisnall the time. For example, space translations have the operator e^(-2pii/hbar*p*a), where p is the momentum operator (usually represented as a derivative operator) and a is the ammount of translation. Actually, for all continuous symmetries you have such operators (rotations, boosts, ...).
@@zoltankurti Do these class of operators have a name? Is QM the only application for such operators?
@@lucagagliano5118 I don't know any special names for them, in the qm kontex they are just ordinary linear operators on a Hilbert space. I can not also say if this is their only application, the only thing I can say is that this is the only place where I've seen them applied.
The derivativeth derivative of a function
ンアーッ! そんな危険なところにDを入れて・・・
と思ったら無限級数の方をいじるのか
いやぁー拡張するの楽しいです
Can you make video series about derivations of e ? That would be very very interesting. Perhaps 2-3 episodes.
/just kidding ;)
So, I know this is more of a comment on my lack of knowledge, but what precisely makes this valid?
5:07 you said you wanted to find the sin-th derivative of cos... But why did you use i?
Garand Chua e^(iθ)=cos(θ)+isin(θ). Therefore, taking the sin(D) operator and allowing it to operate on e^(iθ), you can compare the real and imaginary parts of both expressions (near the end of the video) to get the identification expressions for sin(D) operator acting on the exponential function.
@@robertleeshinkle8446 ok thanks
Infinite derivative?
Dr peyam can u wait a little bit lol when u finish a board before erasing and step a bit aside lol because a lot of us are taking screens hots of the final board lol thanks
I’ll try 😅
I mean screenshots sorry lol
What about i-th derivatives? (And next: complex ones)
Imaginary derivative of x ua-cam.com/video/tMalym_n8zM/v-deo.html
I went and looked at the g[D] of f(x), the general case for these function-derivatives, and I wasn't satisfied with Maclaurin series. It's pretty easy to find that g[D] (f(x)) =
sum n=0 to inf. {
[(D^n)[g] (0)] * [(D^n)[f] (x)] / n!
To get a taylor series, you would write
[(D^n)[g] (h)] * [((D-h)^n)[f] (x)]
That means we've got a binomial expansion to do, which is pretty bad because we've already got a summation. The double summation will not go away cleanly in the end, either.
Starting with the trouble spot (also, it makes more sense to use 'y' instead of 'h' for the end result, for a nifty 'symmetry'):
((D-y)^n) [f] (x)
=" {binomial expansion, (D^k)[f(x)], (-y)^(n-k)} "
and we eventually get
((D-y)^n) [f] (x)
=
(n!) * { sum k=0 to n
(-1)^(n-k) * (y)^(n-k) * [(D^k)[f(x)]] }
Putting it all together would get terribly cumbersome in a youtube comment (it's much cleaner when written properly), but the end result:
- is a double summation that isn't clearly easy to clean up
- contains the product:
[(D^k)[f(x)]] * [(D^n)[g(y)]]
-has an almost mystical 'symmetry,' where switching from
g[D] @y of (f(x))
to
f[D] @x of (g(y))
only switches
[(D^k)[ f (x)]] * [(D^n)[ g (y)]]
to
[(D^k)[ g (y)]] * [(D^n)[ f (x)]]
and changes y^(n-k) to x^(n-k)
-definitely includes the solution where y=0 gives the Maclaurin expansion of g. (There's a tiny trick because 0^0 = 1 for binomial expansions 'like' this.)
[D[f(x)] -y ] ^n isn't very clear notation, which got me caught up in thinking that it wouldn't make any sense (which it still doesn't, but I did use the binomial expansion.)
-D^k [f(x)] is a function of x with parameter k. So long as the output of that function satisfies |D-y| < r {Or = r, possibly}, the series will converge to the function g. The output space of D^k [f(x)] is not a 'function space,' it's a real space. This is true in the case where y=0, as well, as it has to be for any of this to work.- Incorrect, sorry.
I will change my comment to clarify the binomial expansion step.
I don't think it makes sense to consider it a Taylor series when we use (D-y). Convergence to a value can be established for the series, but I don't think there's any way of considering whether the Taylor Series converges to g([something]), partly because the operation isn't supposed to result in a function of g as such.
If the radius of convergence is infinite, it already will 'converge to the function,' to the extent that one might want to answer such a question, but I think you can just use a Maclaurin series if that's the case.
I guess my whole investigation here is moot, overall, then.
Of course. Only a function g with a Taylor or Maclaurin series that converges everywhere will allow you to use the g(D) of f operation. Anything else will be nonsense. This is one of the premises of these videos.
On another note, I think that a notation like
g(d) f(x) /
g(dx)
would cleanly convey what's implied in Leibniz notation. g(x) = x^2 implies d^2 f(x) / dx^2, and results in exactly that through the definition g[D](f(x)) = { g(d) f(x) / g(dx) } = series(...) { [g^(n)(0) /n!]*[f^(n)(x)] }.
Though that particular example just returns the original problem, it makes the whole idea of a Taylor-Maclaurin Function-Derivative, or however you might call it, much cleaner to think about.
Some applications that are trivial are thinking about differential equations as Function-Derivatives, for example:
Given
g(x) = x^2 + 1, f(0) = 0, f is not the 0-function, and g(d) f(x) / g(dx) = 0;
f(x) = sin(x) .
This is pretty trivial, but interesting nonetheless.
For the thumbnail: wouldn't it be "sin(d/dx) x" ?
I know, but the current thumbnail looks nicer
sin(1)=Im(exp(i))
do people commonly call sinh "sinch"? I never heard that before :D
Yeah, they do.
So sin(d/dx) [e^(pi*x)] is just 0. 🤯
Could you please write when you are deriving the function? Because you just wrote something like " function" = "derivative of the function", and it really complicates the comprehension of the video.
How about like arctan(d/dx) lnx?
Same idea, just use the power series expansion of arctan and apply that to ln(x)
@@drpeyam Ok, thx for your reply. How about for a general function f(d/dx)? How will you define it?
Just find the Maclaurin series of f and apply that to the function you want
How about the f(d/dx) is not defined.
That I’m not sure of, but most functions we know in calculus are defined
I think I could do a power series of: x.
Tangent derivative for sin . Its look funny..
Haha this is crazy. I love it.
this is me... what .... ohhh ... cool... the world just got bigger!
I want Gaussian derivative for Christmas please.
There will already be a Xmas special ;)
Does this have any practical use?
Functions of derivatives tend to appear often in quantum mechanics. For example, the time evolution of a system is described by an exponential derivative. Some other more fancy tricks can use sinD, etc.
Happy Yalda Peyam agha 🍉🍎
You too!!!!
@@drpeyam Danke! 👋
But why??? Why would you say that (d/dx)^(sin) =sin(d/dx) in the thumbnail (again!)? That is so wrong it even fails for reals: 2^3=/=3^2.
I love you but this is really frustrating. You don't even acknowledge it. Is it just clickbait? It's frustrating because I would love you to explore the real deal, the actual (d/dx)^(sin).
Sorry, I made the thumbnail one month ago 🙊 I’m gonna change it
@@drpeyam No problem. Thank you for the explanation and for changing the thumbnail. Love your videos. : )
@@angelmendez-rivera351 Hm, (d/dx)^(sin x) and (d/dx)^(sin) might be different things.
Also why e^[(sin x)•Ln(d/dx)], instead of e^[Ln(d/dx)•(sin x)]? I agree with you that the first makes more sense but clearly commutativity fails. If commutativity fails why would you expect (d/dx)^(sin x) =e^[(sin x)•Ln(d/dx)] to hold?
But I'm not being very helpful. Convergence is an issue but defining Ln(d/dx) isn't hard, you just need to take the Taylor series.
On possible definitions. One very boring definition would be (d/dx)^(f)(h)=[(d/dt)^(f(x))(h)]|(t=x). Where [(d/dt)^(f(x))(h)] is a function of the variable t.
What I would like to be true is that (d/dx)^(f)(d/dx)^(g)=(d/dx)^(f+g).