Germany || A Very Nice Math Olympiad Problem | Solve for the value of x

In this video, I'll be showing you step by step on how to solve this Olympiad Maths Exponential problem using a simple trick.
Please feel free to share your ideas in the comment section.
And if you are new here and you enjoy my content, please hit the like button and subscribe to my channel. Don't forget to hit the bell icon as well so you don't miss on my upcoming videos.

[@JakeMarley-k6g]

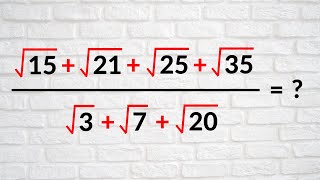
Interestingly, Desmos thinks there is only one solution to the equation

[@SrisailamNavuluri]

x^3+x^2=x^2(x+1)=4/27=1/9(4/3)=(1/3)^2(1/3+1
x=1/3.
Lhs=4/9(1/3)=(-2/3)^2(-2/3 +1)
x=-2/3.

[@SpencersAcademy]

Excellent delivery 👏

[@JyotiradityaDwivedi-j6e]

X^3 + X^2 - 4/27 = 0 --- (1)
X = 1/3 ( by trial and error )
divide eq (1) by (x - 1/3)
get the other value of x as -2/3 and -2/3 ( twice )
so finally three values of x are 1/3 , -2/3 , -2/3
Edit - personally i think this is a better way and quicker way , let me know if im doing something wrong

[@SpencersAcademy]

Fantastic

[@CharlesChen-el4ot]

x^3 + 1 = 3/27 - x^2
(x+1)(x^2- x+1) =
1/9 * (x+1)*(x-1)
9 x^2 -9x + 9 = x - 1
9 x^2 - 10x + 10 = 0
x = 1/18 * (( 10 +-(100-40)^1/2)

[@walterwen2975]

A Very Nice Math Olympiad Problem: x³ + x² = 4/27; x =?
x³ + x² - 4/27 = 0; (x³ - 1/27) + (x² - 3/27) = [x³ - (1/3)³] + [x² - (1/3)²] = 0
Let: a = 1/3; [x³ - (1/3)³] + [x² - (1/3)²] = (x³ - a³) + (x² - a²) = 0
(x - a)(x² + ax + a²) + (x - a)(x + a) = (x - a)(x² + ax + a² + x + a) = 0
x - a = 0, x = a or x² + ax + a² + x + a = x² + 4x/3 + 4/9 = (x + 2/3)² = 0, x + 2/3 = 0
x = 1/3 or x = - 2/3; Double root
Answer check:
x = 1/3: x³ + x² = 1/27 + 1/9 = 4/27; Confirmed
x = - 2/3: - 8/27 + 4/9 = 4/27; Confirmed
Final answer:
x = 1/3 or x = - 2/3; Double root

[@SpencersAcademy]

This is fantastic 👏

[@youssefelyousfi4929]

x=(-2/3)