A Nice Math Olympiad Problem | Two Paths to Success

A Nice Math Olympiad Problem | Two Paths to Success
Join us as we delve into a fascinating Math Olympiad problem that offers two distinct paths to success! In this video, we explore a challenging problem and demonstrate two different approaches-one through algebra and the other through trigonometry. Whether you're a math enthusiast or preparing for a competition, this video offers valuable insights into problem-solving strategies. Discover the beauty of mathematics as we navigate through this intriguing problem together!
🔍 In this video, you'll learn:
Strategies to approach challenging Hexic equations.
Step-by-step solutions explained with clarity.
Tips and tricks to make algebraic problem-solving feel like a breeze.
Gear up for an enlightening journey with trigonometry into the world of algebraic challenges!
🌐✨ Subscribe now and empower your math-solving skills.
#mathematics #matholympiad #problemsolving #algebra #trigonometry #competitions #mathenthusiasts #mathematicseducation #learningmaths #problemsolvingskills #stem #mathematicschallenge
Thanks for watching!!
@infyGyan

[@NadiehFan]

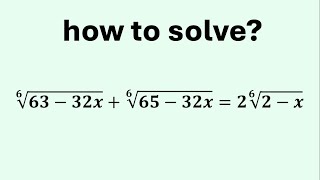
At 1:02 where you have arrived at
16x⁶ − 24x⁴ + 10x² − 1 = 0
it would have been much smarter to start by multiplying both sides by 4 to make the leading coefficient 16 into a cube 64 = 4³ because then we have
64x⁶ − 96x⁴ + 40x² − 4 = 0
which we can write as
(4x²)³ − 6·(4x²)² + 10·(4x²) − 4 = 0
Substituting
t = 4x²
then gives
t³ − 6t² + 10t − 4 = 0
which is a _monic_ cubic equation. This makes it much easier to apply the rational root theorem, because any rational solution of a monic polynomial equation with integer coefficients must be an integer.
Also note that the coefficients of the _odd_ powers of this cubic are _positive_ and the coefficients of the _even_ powers of this cubic are _negative_ which means that the left hand side is negative for any t < 0. Consequently, this equation cannot have negative roots. So, we _only_ need to test the positive integers 1, 2, 4 as potential rational roots, and then we quickly find that t = 2 is a solution of this equation.
In accordance with the factor theorem this means that the left hand side has a factor (t − 2). Factoring this cubic is now easy if we subtract 2³ − 6·2² + 10·2 − 4 = 0 from both sides, which gives
(t³ − 2³) − 6(t² − 2²) + 10(t − 2) = 0
(t − 2)(t² + 2t + 4 − 6t − 12 + 10) = 0
(t − 2)(t² − 4t + 2) = 0
t − 2 = 0 ⋁ t² − 4t + 2 = 0
t = 2 ⋁ (t − 2)² = 2
t = 2 ⋁ t = 2 + √2 ⋁ t = 2 − √2
Since t = 4x² and therefore x = ½√t ⋁ x = −½√t this gives
x = ½√2 ⋁ x = −½√2 ⋁ x = ½√(2 + √2) ⋁ x = −½√(2 + √2) ⋁ x = ½√(2 − √2) ⋁ x = −½√(2 − √2)
as the solutions of 16x⁶ − 24x⁴ + 10x² − 1 = 0.

[@StaR-uw3dc]

Nice problem and solutions.
In method 1 substitution t=2x^2 would make calculations easier.

[@richardleveson6467]

The second solution is very creative - reminiscent of Newton's method for solving the cubic. Thank you!

[@mohammedsaysrashid3587]

A wonderful explanation...thanks for sharing Sir 🙏

[@infyGyan]

Thanks for liking🙏