Conceptual understanding of flux in three dimensions | Multivariable Calculus | Khan Academy

Courses on Khan Academy are always 100% free. Start practicing-and saving your progress-now: www.khanacadem...
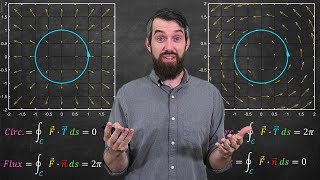
Conceptual understanding of flux across a two-dimensional surface
Watch the next lesson: www.khanacadem...
Missed the previous lesson?
www.khanacadem...
Multivariable Calculus on Khan Academy: Think calculus. Then think algebra II and working with two variables in a single equation. Now generalize and combine these two mathematical concepts, and you begin to see some of what Multivariable calculus entails, only now include multi dimensional thinking. Typical concepts or operations may include: limits and continuity, partial differentiation, multiple integration, scalar functions, and fundamental theorem of calculus in multiple dimensions.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to KhanAcademy’s Multivariable Calculus channel:
/ channel
Subscribe to KhanAcademy: www.youtube.co...

[@hadijaffri9856]

Man i swear this guy knows everything.I have been listening to his lectures from 10th grade,now im in university.Is this dude sheldon cooper with a masculine voice?

[@Timmy-zl1gu]

yes he is

[@Timmy-zl1gu]

or DR stugis

[@wyatttomlinson3475]

This video singlehandedly made flux cool! Thank you so much Sal! This semester of Calculus 3, you have made the concepts simple to grasp, sure, but more importantly, fascinating!

[@ritabratochatterjee6881]

Khan academy is one of the several sources from where I happen to get the most authentic lectures on topics. Thank you.

[@TheTokyoExpress]

you only hate it because you had teachers that were poor at teaching it

[@geetarwanabe]

If you throw the ball perpendicular to the wall (100% in the normal direction) then your dot product F(dot)n would be 1, result in no loss in your mass flux so 100% of your ball would pass in say 1s
If you throw a ball at an angle, say 10*,then your dot proct would result in (0.92 at a guess)so only 92% of your ball will pass through in the same time period
So yes, the same amount of mass would eventually pass through but the flux has changed. Its reduced. So we are only interested in normal.

[@johnmesserly4051]

you're so good at drawing things jesus

[@musataz]

yep he is but what did he draw here?

[@brothertrucker4820]

he was talking about Jesus and how good he can draw

[@salmagamal5676]

my love and gratitude for this channel is just infinite

[@SalsaTiger83]

The vectors that are orthogonal to the surface normal are "on" the surface, so if a partical travels on them, it doesn't "flux" through the surface. (I might be wrong, I'm no physicist)

[@ManojKumar-cj7oj]

You're absolutely correct, bcuz I'm a physicist 😁

[@starRushi]

Explanation for flux, if you don't understand it.
So two ways of understanding the relationship between mass and volume
Both say much mass is in a given volume
But one evaluates the volume using density [measuring three dimensions of space] and the other using flux [two dimensions of space, one of _time_ ].

[@gavi7v]

3 50 minute lectures summed up in 8 minutes

[@cravenhammock5401]

The one aspect I don't understand intuitively is taking the dot product. Why is it that the part of the flux (F) which is orthogonal to the surface normal (n) is excluded (by taking the dot product.
If I throw a ball through a doorway at an angle other than the doorway's normal its entire mass still passes through that surface.

[@adityaprasad465]

Imagine a volume of water flowing through that door. If it's not flowing normal to it, then _less_ mass gets through.

[@Civsuccess2]

Flux capacitor!!!! Great Scott!!!

[@RougeSamurai77]

Wow, this comment is old.

[@lamp0]

@@RougeSamurai77 Wow, this comment is old

[@raphaelramos4016]

Wow, this comment is old

[@rogacz935]

@@raphaelramos4016 wow this comment is old

[@midnightsun1429]

@@rogacz935 wow this comment is old

[@ilikefootballandbaddecisions]

Thank you!!!

[@geetarwanabe]

When you take the dot product you are seeing exactly how much ( or I guess you could say "what component" ) of your vector is pointing in the DIRECTION of the dotted vector.
Lay your head on a desk, place your hand off and to the side of it. Raise your hand vertically, then repeat at some angle. Notice how the speed at which your hand is rising has changed i.e some component is orthogonal, REDUCING the mass flux that is normal.
So F.n tells your how much mass is leaving/entering your surface

[@syabongajele6431]

thank you

[@arsalansyed4709]

holy crapp!!!! Thank you so much!!!!

[@stephenma5563]

this is awesome!

[@TheMornom]

awesome explanation.

[@andrerossa8553]

nice, tks

[@NeedSaltForFries]

excuse me, Mr Khan, but can you please do a module on a simple paradox?

[@alexander-p1f]

is F a vector field?

[@harshithatwal8293]

and to understand electric flux

[@vipeshrajput]

gud intuition

[@amitt111]

i loveee you !
thanks alot !!!

[@joerosati5017]

not bad

[@harshithatwal8293]

which chapters should i study to understand what is double integral please reply sir ............................

[@alejandroochoa5165]

chapter 2

[@madhavbovilla7363]

video is just appearing as green screen though the explanation is pretty good

[@VinothKumar-qo7ry]

Nice

[@HockeyMan-kd7yj]

Should be titled "5minuteFlux"

[@yuri778]

Gah I hate physics....but at least I learned something.

[@dapianoman03]

great explanation, but this guy repeats things too much

[@neilzep]

4 th comment