Destroying the Gaussian Integral using Papa Leibniz and Feynman
Вставка
- Опубліковано 7 лют 2025
- Help me create more free content! =)
/ mathable
Merch :v - teespring.com/...
www.amazon.com...
shop.spreadshi...
Leibniz Rule: • The Leibniz rule for i...
Fresnel Integrals: • An Insane Approach! Th...
Some people are accurate and call it using the Leibniz rule, some aren't and are calling it Feynman integration. Neverind that, let's continue Papa Flammy's integral week with a famous one: The Gaussian Integral including a constant in the exponent =)
2nd Channel: / @rockhardwooddaddy
--------------------------------------------------------------------------------
Wanna send me some stuff? lel:
Postfach 60 06 03
14406 Potsdam
Brandenburg
Germany
--------------------------------------------------------------------------------
My Website: www.papaflammy...
Instagram: / flammablemaths
Flammy's subreddit: / flammybois
Twitter: / flammablemaths
Facebook: / flammablemaths
Got some time to spare? Make sure to add captions to my videos! =) www.youtube.com...
Want to know more about me? Watch my QnA! =D • Question and Answer Ti...
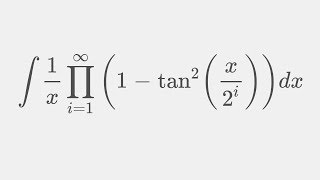







In approximately 1971 I attended a seminar by Feynman on the PCT theorem at UC Berkeley. The auditorium had sliding black boards as in this video except that they were huge and heavy and so they hung from pulleys with one of the boards serving as the counterweight for the other. Feynman, upon sending up one of the boards to write on the other said to the audience "Oh look. I don't have to do any work." Laughter from the all-physicist audience.
I just discovered this channel and I freaking LOVE IT. Flammable Maths is awesome!!!
Flammable Maths enjoying is an understatement! :D
14:29 This is outrageous
Gaussian represents some sort of symmetry which in 3-d can be built up by infinitely many slices of "disks". With that, it, no wonder, is somehow related to Pi.
I like how in these older videos you make a few more mistakes, still the content is great do like it very much! Papa bless
:)
10:41 the best thing to do as a german... xDDD
DON'T MENTION THE WAR!!!! :)
Godwin point my bois
Maks not C!
As a german, and behalf of all Germans
We will remember this flamy, and so will the wall street journal
*Sips* Reminds me of the time when Kant tried to destroy traditional metaphysics
Hahahha yeah, that was indeed funny.
More so. I don't think its so much of Kqnt trying to destroy traditional metaphysics than it is him being irresponsible epistemology
Nothing less than a cool video! Haven't learnt some of these integration techniques yet, so I know how I'm gonna spend this evening!
10:04 mah boi's board has been possessed by Papa's soul.
14:14 OMG that celebrity's name is Sharukh Khan and my mother was his fan and that's why she named me Sharukh. Coincidence? I think not.
You are a genius. Period. Just shared this video with 5 others
Alright,I wont be going to school now...Watching ur videos is enough
lol
Thanks for this video man! Keep going u are the best
Greetings from America and Africa! Have a Flammable day, bro! 😊🙌🏽🎊
Hi there, dude. Love your vids. At minute 14, what if the parameter "a" is negative? Wouldn't it lead to a non convergent integral? Brilliant! Keep going.
yes, a>0 is required!=)
Thank you... It is helpful in solving quantum mechanics problems
2:59 the CHEN LUUU!
14:13 Great picture of Dr. Peyam.
Is he Shahrukh Khan from India?
@@all462 yuuup
Ok but it works only if a>0 !!
Or Re(a)>0
@@aidankwek8340 Integral wont converge in all cases
Mathematics sounds so much better on chalk than a marker board
Subbed and favorited immediately upon seeing "Papa Leibniz". Haven't even watched the video yet and I still can't do calculus.
I allays wondered what π have to do with this integral
The moment i saw Invers tan i felt it
Thank you very much 🥰
finally a solution that i can understand
I am a high school student by the way
At 7:48
Don't forget the negative sign my boys!
Jens : 'My girls' are smart. Only boys need a reminder!
😂
:D
*Papa* ...
I miss you and your Math ....
Therefore I'm here, because your old videos are still great.
Thank you *Papa Flammy Mathy* .
*Papa's Ways, Is The Best* .
Your Hagoromo Chalk and Your black jacket 😂
i like how it sounds like a youtube apology video in the beginning
Had to come over here and hand out a like, just because of the title.
:D
13:37 This limit, we'll dominate :)
1337
i got asked to solve this for an interview and i am going to use this next time i get asked to BLOW SOMEONE'S MIND.
It must be so fascinating, any dislike in your videos i guess, thats a proof that your channel its a lot useful, fellow :)
Oh my god!!! Gauss could be angry :v.
Just amazing!
You look angry in the video debut 😂😂 I like you 🔥
I am from india....this concept come so many times in gate exam ...tq brother...🙏🙏
That's some nasty integral
If a
PHYSICS STUDENTS: change to polar coordinate plane --> done
I LOVE YOU
Watching you do this is very satisfying. Where did you learn these techniques? In graduate courses? I'm an engineering student but these techniques are never mentioned in my calculus classes.
I have learned how to solve exponential equations lately. I faced a problem that required a substitution t=2^x and t ended up being negative. Well, no problem, complex numbers helped me and I got the result. My teacher had never heard about such a thing. Note she has a masters degree. Thank you, mathematicians of UA-cam.
where do you find such thorny integrals? I'm looking for some hardcore calculus questions...
@@SirDerpingston e^[-(x)^2] is a famous function because 1.) It is the general shape of bell curves used in statistics and 2.) It's integral is non-elementary, which I find pretty interesting
@@PapaFlammy69 , that's the only way to really LEARN , DO & UNDERSTAND maths ... !!! ... & you also 'did well' , so thanks !
@@SirDerpingston michael penn on yt and this channel have some meaty integrals
I found the general method, it is more geometric
it change I(x) to (I(x))^2=I(x)I(x*)=I(x)I(y)=V(x,y)
so we need to integrate z(x,y)=e^((-a)(x^2+y^2)), plot on 3 dimension
the integral basically is finding the volume between z(x,y)=e^((-a)(x^2+y^2)) and z(x,y)=0
we found symmetry around z axis, so we change the coordinate to cylindrical coordinate
the original integral=z(x,y)dxdy=e^((-a)(x^2+y^2))*dx*dy
intergral after=z(R,angle)dRd(curve)=e^((-a)R^2)*dR*(Rd(angle))
the additional R from d(curve) made the integration solvable
them I(x)=(I(x)I(y))^0.5, solved
I still like your method more
Your method is much easier to understand
Making a bit complicated but I love your approach ...
Extremely a mad genius
You know what would actually be good, is if you can use guassian blurs to do filters instead of IIR/FIR if you can just increase the fall off!!!
you could do it in one action by dividing and multiplying by the root of A and substituting A under the differential
nice approach.
Are you interested only in real/complex analysis? What about Abstract Algebra, Combinatorics, Topology, Number Theory etc...?
why does he feel like crying but resisting it the best he can
Don't you have to use uniform convergence in order to interchange integral and limit at 13:25? Because that's not allowed in general. For example, observe the integral from 0 to 1 of n*x^(n-1) dx and let n go to infinity.
i love you papa flammable maths;
great video!
Man you're so cool and handsome
lol, you approach the problem of interchanging various limiting processes as every professional analyst I know: "just fuck it"
but the video and technique are lit af
if Gauss revives and sees this bad boi he will get mad indeed :v
At 2:00, how did we know to square the I(t) integral? Like, trying to solve it, what clues are there that this is a useful step?
Lovely stuff
Nice picture of Dr Peyam
AndDiracisHisProphet where?
AndDiracisHisProphet nvm got it at 14:14
@@blackpenredpen That's actually the Indian actor Shah Rukh Khan
3:08 There is just one term there equal to exp(-at^2) by the usual fund. thm. of calculus.
1:32 We call that bad boy "you""? OK, if you insist.
Thanks for the video!
7:30 The u=x/t therefore it is dependent on t, how could you ignore the chain rule in the partial differentiation step?
Lookin rough, my guy. You doin ok?
This could also be solved for by using the gamma function (a lot easier imo)
NICE! I only missed what if a
I know that pi is half a circumference. was he talking about circles?
San Samman a circle is 2pi radians, radians is standardized in the unit circle so it’s just 2pi
Why tan^{-1}(x)? Why? arctan(x) is so much better ! tan^{-1}x=1/tan(x)=cotan(x) ! Other than that, great video.
context, my friend
also i think it is important to remember that "to the minus 1" doesn't mean "1 over" but "inverse".
It just happens that the inverse of simple numbers is also denoted as "1 over"
inverses are just weird in trigonometry. go look up:
pre algebra.
I'm kidding 😂
Wow really awesome
Hey I just wanted to ask about when you are solving for the c value, you don't touch the variable u even though it is dependent on t. As I recall, t is equal to zero, and u is equal to x/t, which would make u undefined. I would just like to ask how it still works even though that part is unresolved.
Thank you so much for your effort and I'm loving your videos!! There really is a uniqueness to your videos that I don't think I've ever seen except kind of in Faculty of Khan, who is just pure salt and no more.
This really blew my mind on several levels, so I'll use papa flammy's method every day in my calculus class, referring to it with that name every time because there is no other more beautiful way to describe it.... I don't know how but I'm going to try anyway XD.
Me after watching the first episode of Rick and Morty
"is nothing else but", is nothing else but, "is just".
ie. "is nothing else but" simplifies to "is just".
XD Sorry I couldn't resist a silly joke. :P
In the beginning of the video you state that a is in the real numbers, but later on you use that the limit of t -> infinity of e^(-at^2) = 0. If a is negative, this does not hold anymore.
The proof still holds for a>0 of course and it is still beautiful.
Do correct me if I'm wrong though.
Partial derivative, t and +c: Hey
Me: Have mercy please
Them: There is no mercy
Also the only thing in this that makes sense is dt/dt=1, the rest just makes no sense, sik why calculus was even a thing, like it makes no sense
now I know why my professor don't want to proof this in class XD the way is kind of tricky for me, especially the the integral at the last part vanish when t close to infinity. I was like "wait, whaaaat?"
Actually, I got a little feedback
I don't really have too much talent in calculation. So yeah, I ran into a lot of issues in learning.
The good thing is I would know exactly what it takes for a normal person to understand this kind of proof.
When I'm trying to understand any proof and analysis, I always struggle in why do this now, why do that now, and somehow it just work out. In this kind of situation, I usually would look the proof several times to find reasons to makes the method make any sense. But sometimes it just really hard to figure it out. But only by doing this I can really apply this method (or even figuring out a method) in other problem.
My suggestion is make a summary after the derivation, going back and explain why do this now, why do that now. But this might be why watch you derive is better than on textbook. Sorry for bad grammar, English is not my native language. I hope this will help you out:)
Is it possible to evaluate integral e^-(x^3) 0 to infinity the same way?
Nice video! Why did you use the same letter (I) for constant and for function?
This was super cool. However I have a problem:
You introduced u as x/t and then you treated u as a separate variable, for example, when you took the limit as t goes to infinity.
Are we allowed to do that? I mean you got to the correct answer, so I suppose there must be some validity in what you have done...
Dont say that - you easily get correct results from doing wrong maths, so your question is legit. My guess looking at it would be that you got lim t²(u²+1) = lim t² = inf (because lim u²t² = constant) and lim u²+1 = 1 and thats why he doesnt even mention that u = u(t).
*Link in the description to the corresponding video* 😂😂😂 Yes bro
a belongs to R.Doesn't that mean that when a is negative the integral is not finite?
Hello. I'd like to ask why u was considered a constant at 7:15 when u was defined as x/t. Thank you.
Just watch this impressive Math channel ua-cam.com/channels/ZDkxpcvd-T1uR65Feuj5Yg.html
At 12:00, if we make t = 0, doesn't that mean u = x/0 which isn't allowed?
fellow mathematicians
fllow mathemacians
flow mathemains
flo mathmans
flo mamans
flo amas
fl amas
flamas
= flammers
Holy, you looked so tired 2 years ago!
Shouldn't the domain of a be a>=0? If a∞) doesn't converge, right?
yas!
@@PapaFlammy69 Thanks for quick answer, Papa Jens
Papa Bless
Good morning to you too my flammer
Area property of Fourier transform doesn't give correct answer for this integral. Why?
I mean this property, area under the curve of f(t) = F(0).
Lord Kelvin's definition of a mathematician:
Someone to whom Int[-infty, +infty] exp(-x^2) dx = sqrt(PI) is as obvious as 2+2=4.
(Said before Russell and Whitehead rendered 2+2=4 non-obvious to anyone.)
Papa's way is the best
Legends only know that he was earlier known to be "Fapable maths"😂😂😂
Brilliance incarnate.
why is the comments section blocked for the new videos, does any one know???
Can you solve the integral of x².e^2x² dx from -infinite to +infinite?
Wow, square the original integral (dx dy), switch to polar coords, and this joint is much easier.
14:14
Are you a fan?
Or just used the photo for no reason?
But you still used the squaring trick. How about doing it purely with a parameter and differentiation under the integral?
14:16 Did you consider the case which a
great .thank you .... is x variable real or complex ?
a must be positif because of the square root
What can be done about the quotient of two of them? Like one integrated until 3 and other until 5, or so?
Can you say where is a in graph ?
I have a question. at 12:00, if we make t = 0, doesn't that mean u = x/0 which isn't allowed?
Did you ever solve this question? I am having the same problem understanding.
@flammablemaths @YourMakingMeNervous
4 years late but that integral was in terms of x, so we're plugging 0 into x, and t into t.
4:10 MY EYEBALLS!!!
Damn this is awesome. Verstehe nur manche sachen nicht ganz mit dieser Partiellen Ableitung das wurde mir zu schnell aber sonst hammer video. Das liebe ich so an mathe. Richtig komplizierte Integrale und dann so eine schöne Antwort 👍
a should be different to -1 i think
genius papa
I've gotta know, what song do you use whenever you introduce the problem?