TRIANGULAR LOAD Shear and Moment Diagram EXAMPLE PROBLEM // Calculus Explained

In this video I go through an example problem of drawing shear and moment diagrams of a beam that has a triangular load on it.
Check out some awesome Student Engineering merch!
teespring.com/...
amzn.to/33QseWz
amzn.to/3kAWPNE
Quick Tips (I explain these in more depth in the video)
The area under the loading curve = the change in shear (positive area is a positive change and negative area is a negative change)
The area under the shear function/diagram = the change in moment (positive area is a positive change and negative area is a negative change)
Positive slope on the loading function = concave up shear function
Negative slope on the loading function = concave down shear function
Positive slope on the shear function = concave up moment function
Negative slope on the shear function = concave down moment function
Distributed load intensity = the slope of the shear function
Amount of shear = slope of the moment diagram
Where the shear diagram crosses the axis is a max or min on the moment diagram
Drawing shear and moment diagrams process:
1) Establish your coordinate system with the positive X direction being along the length of the beam, starting on the left.
2) Solve for the support reactions on the beam using moment equilibrium equations and force equilibrium equations in the Y direction.
3) Draw the free body diagram of the beam with the solved support reactions written as forces as well as the loading scenario.
4) Draw the shear X axis and the moment X axis vertically aligned below the beam to line up the changes of the loading with the shear and moment diagrams. Then label these diagrams with V for shear and M for moment and label the units for each.
5) Plot the shear diagram starting from the left end. As you encounter forces in the loading scenario, draw the shear diagram as outlined in Note A. Label the distance X along the diagram where the shear function crosses the axis.
6) Plot the moment diagram starting from the left end. As you encounter changes in the shear diagram, draw the moment diagram as outlined in Note B. Label magnitude of the moment at the maximum and minimum points along the function as well as what point along the X axis they occur.
Note A:
A point load (a force at a single point) causes the shear diagram to jump straight up or down; up if the load is pushing up and down if the force is pushing down. This includes reaction forces. Point moments will not directly effect the shear diagram.
Distributed loads cause the shear diagram to decrease or increase in a way that can be modeled by a function. You can model the distributed load as a function and then integrate that function to get the shear function (see the Quick Tips at the top for more specifics on this).
Note B:
-The moment reactions at the ends of the beams are zero if the beam is supported by pin, roller or free connections. This means that the moment diagram will start and end at zero. However, if there is a fixed support then there will be a moment reaction which will cause the diagram to not start or end at zero, depending on which side the fixed support is on (usually it is on the left end). If there is a support reaction then it will cause a vertical jump in your moment diagram just as a point moment would. Remember that the support reaction is in the opposite direction of the internal moment. If the support reaction is counter clockwise (positive) then the internal forces which you are drawing are negative and thus will have a negative drop.
A point moment will cause a vertical jump. The direction of the jump being as explained in the previous point.
The integral of the shear function is the moment function. This only applies to sections of the function that are continuous, in other words, there are no vertical jumps up or down
(see the Quick Tips at the top for more specifics on how to draw the diagram).

[@Gerry363c]

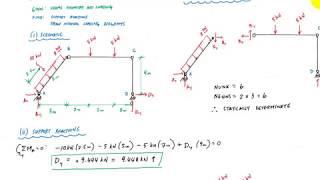
Confusing in finding the sum of the moments..more explanation needed. Thanks by the way

[@studentengineering]

Watch this video and see if it helps: TRIANGULAR LOAD Shear and Moment Diagrams EXAMPLE PROBLEM
ua-cam.com/video/imLU3O791PQ/v-deo.html

[@Gerry363c]

@ thanks

[@Johndavid1451]

Thanks for the video, man! Flipping the triangular load upside down really helped me in understanding the moment and writing the shear equation.

[@studentengineering]

Yea when I finally figured out that it worked like that it made a huge difference in how I understood triangular loads. I’m glad you found it helpful!

[@jamesandrews7426]

Why multiply 450 with 1? I understood the centre of gravity for the right angled is 1/3 its length, but since you took moment at point A, shouldnt it be 450x1/3? Because its 1/3 away from point A?

[@studentengineering]

Great question! You’re right that it should be 1/3 along the triangle’s length. Because the triangle is 3 ft long that comes out to be 1

[@youssefelbanna711]

Hello, I love your videos they make this topic so clear! However I have a simple question. When you write the equation w(x) for the triangular distributed load, when is it -300, not 300? I am talking about the intercept or whatever you are going to call it. How do you decide on the sign?

[@studentengineering]

Thanks! I’m glad! When the force is going down I write it as negative and when it is going up I write it as positive.

[@youssefelbanna711]

@@studentengineering Thank you for the response. Usually all distributed loads go downwards, does that mean that I will always have the w(x) intercept as negative?

[@studentengineering]

Yes

[@kenmalacinski8442]

I am confused on why 3 is being plugged in instead of 6. I am getting different boundary conditions but ending up with the same max moment of -2250. I see you are defining the part where the triangular distributed load starts as 0 on the x axis? Why isn't this defined as 3 on the x axis?

[@studentengineering]

I think we just summed moments about a different point. Does that make sense?

[@SignMusic13]

Thanks for the video!

[@studentengineering]

You’re welcome!

[@frozenporcupine]

thanks man. great example used

[@studentengineering]

Thanks!

[@40Ksigmar]

Why did you use By instead of Ay for the Sum of moments A please?

[@studentengineering]

Great question! When we sum moments about a point we don’t need to include forces that pass through that point. This is because those forces won’t cause rotation about that point. When you sum moments about a point to find reaction forces you want to pick a point that is in the line of action of as many unknown forces as possible so that you don’t have to consider them in that particular equilibrium equation. Besides that reason, it doesn’t really matter which point you choose to sum moments about.

[@avachar11]

Nice. Thank you

[@studentengineering]

You’re welcome!

[@zana.m.rashid6747]

I liked 👍

[@studentengineering]

I’m glad!

[@jacksonhilsabeck9109]

for the moment equation why do you plug in 3 and not 6?

[@studentengineering]

Great question! That would be the case if the moment equation described the bending moment across the whole beam but it doesn’t. The equation describes the moment starting at 3 feet along the beam and going to 6 feet along the beam, moving from left to right. This is where the triangular distributed load occurs and so plugging 3 into the moment equation gives us the moment that occurs 3 feet along the section of the triangular distributed load but 6 feet along the beam. Does that make sense?

[@zana.m.rashid6747]

🔥🔥

[@studentengineering]

Thanks!

[@pepito8685]

😂😂😂😂😂😂😂😂😂😂😂😂😂😂😂😂

[@studentengineering]

What’s so funny?

[@kevinplug6059]

You ​@@studentengineering made it easy🎉🎉