Let's Solve A Challenging Exponential Equation for All Reals
Вставка
- Опубліковано 26 чер 2024
- Hello My dear family I hope you all are well if you like this video about Solving an Challenging Exponential Equation for Math Olympiad Preparation then please do subscribing our channel for more mathematical adventures like this.
Let's Solve A Challenging Exponential Equation for All Reals
In this video, we tackle a challenging exponential equation and solve it for all real numbers. Join us as we explore different techniques and strategies to find the solution. Whether you're a math enthusiast or preparing for exams, this step-by-step tutorial will enhance your problem-solving skills and deepen your understanding of exponential functions. Don't forget to like, subscribe, and hit the bell icon for more math challenges and tutorials!
Topics covered:
Exponential equations
How to solve exponential equations
Algebra
Algebraic identities
Exponential Equation
Math Olympiad preparation
Math Olympiad training
Exponent laws
Quadratic equation
Factorization
Algebraic manipulations
Real solutions
Timestamps:
0:00 Introduction
1:40 Exponent laws
2:36 Substitutions
5:42 Algebraic identities
9:11 Solutions
9:25 Verification
#mathchallenge #exponentialequations #mathtutorial #algebra #problemsolving #mathhelp #learnmath #mathforall #equationsolving #stem #matheducation #studytips #mathtricks #math
Don't forget to like this video if you found it helpful, subscribe to our channel for more Olympiad-focused content, and ring the bell to stay updated on our latest math-solving sessions.
Thanks for Watching !!
@infyGyan



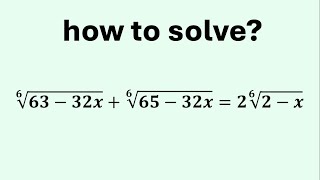





Nice solution.
Other approach: AM-GM: (a⁴+b⁴+c⁴+1)/4 ≥ (a⁴∙b⁴∙c⁴∙1)^(¼) = abc. Equality holds only when all four terms are equal ie. a⁴=b⁴=c⁴=1. Hence x=0.
A wonderful introduction and explanation.....x=0
Great method 😊❤❤
I appreciate the very clever algebraic manipulations. But x = 0 is obvious by inspection. Any expression of similar exponential form in which the numerator and denominator are equal if x = 0 could have been posed as a problem. Proving uniqueness of x = 0 may be a challenge, though.
X=0. By inspection of constraints, it is the only possible solution.
X=0
At 6.0 minutes, each individual bracket is equal to 0 is one possibility and that leads to the solution, x = 0.
But there are three other possibilities that I will try to solve, when one bracket is 0, other two brackets can have opposite sign.
But square cannot be negative hence all equal to 0
x=0 is a solution 😊❤