Evaluating the definite integral using must know basic techniques

Mis-2640
Integrate (x + 1)tan x/(1 + tan x)^2 dx from 0 to π/4
#calculus #definite_integrals #properties #substitution #cipher
Angevin - Thatched Villagers by Kevin MacLeod is licensed under a Creative Commons Attribution 4.0 license. creativecommon...

[@raghvendrasingh1289]

👍
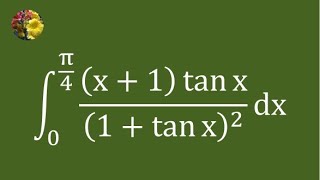
I = integral of (1/2)(x+1) (sin 2x)/(1+sin 2x) in [0,π/4]
replacing x by π/4 - x
I = integral of (1/2)(1+π/4 - x) (cos 2x)/(1+cos 2x)
= integral of (1/4)(1+π/4 - x) { 2 - (sec x)^2 }
using IBP t by taking (1+π/4 - x) as first function)
I = (1/4)(π/2 - 1) + (1/4) integral of ( 2x - tan x)
= (π/8) - (1/4) + (1/4) { x^2 + ln cos x }
= π/8 - (1/4)+(π^2)/64 - (1/8) ln 2

[@cipherunity]

It is done

[@holyshit922]

First calculate auxiliary integral
tan(x)/(1+tan(x))^2 = 1/2*2tan(x)/(1+tan(x))^2 = 1/2*((2tan(x)+1+tan^2(x))/(1+tan(x))^2 - (1+tan^2(x))/(1+tan(x))^2)
=1/2*(1 - d(1+tan(x))/(1+tan(x))^2)
=1/2(x + 1/(1+tan(x)))
Then integrate by parts with
u = (x + 1) and dv =tan(x)/(1+tan(x))^2 dx
1/2 (x + 1)(x + 1/(1+tan(x)))|_{0}^{1} - 1/2\int_{0}^{1}(x + 1/(1+tan(x)))dx
and we have quite easy integral to calculate

[@cipherunity]

It is done.