Відео

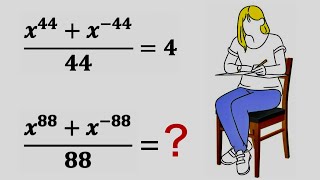
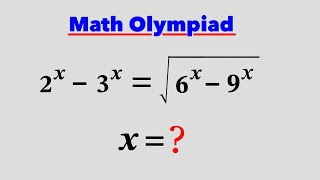
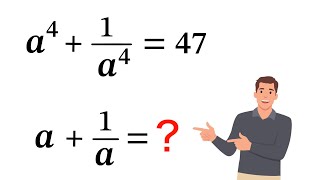
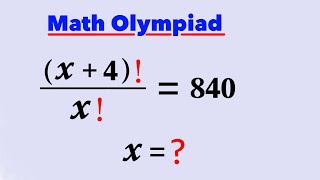
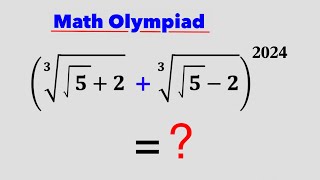
(x⁴⁴ + x-⁴⁴)/44 = 4 (x⁸⁸ + x-⁸⁸)/88 = ? x⁴⁴ + 1/x⁴⁴ = 4*44 (x¹¹)⁴ + (1/x¹¹)⁴ = 4²*11 Let, (x⁸⁸ + x-⁸⁸)/88 = k k = {(x¹¹)⁸ + (1/x¹¹)⁸}/88 = [{(x¹¹)⁴ + (1/x¹¹)⁴}² - 2]/88 Recall, (x¹¹)⁴ + (1/x¹¹)⁴ = 4²*11 k = [(4²*11)² - 2]/88 = (4⁴*11² - 2)/88 = 30,974/88 = 2*17*911/8*11 = 17*911/4*11

x^4-=-1 a^777= a^194×4.a=(-1)^194×a= a ?= a,+1/a= √2

SENSATIONAL!

First we simplify by 2022^2, it gives: 2022(-x) + 2022^x = 2 or 2.cosh(x.ln(2022)) = 2, or cosh(x.ln(2022) = 1. That gives an unique solution: x.ln(2022) = 0 or x = 0. (As cosh(X) = 1 is equivalent to X = 0)

Excellent example 👏

[(x^44+1/x^44)/44]^2=(x^88+1/x^88+2)/(22*2*44)=16 Thus, (x^88+1/x^88)/88=(16*22*44-1)/44=15487/44

?={ (176)^2-2}/88= 15487/44

2ⁿ - 3ⁿ = √(6ⁿ - 9ⁿ) 2ⁿ - 3ⁿ = √{3ⁿ(2ⁿ - 3ⁿ)} (2ⁿ - 3ⁿ)² = [√{3ⁿ(2ⁿ - 3ⁿ)}]² (2ⁿ - 3ⁿ)² = 3ⁿ(2ⁿ - 3ⁿ) (2ⁿ - 3ⁿ)² - 3ⁿ(2ⁿ - 3ⁿ) = 0 (2ⁿ - 3ⁿ){(2ⁿ - 3ⁿ) - 3ⁿ} = 0 (2ⁿ - 3ⁿ)(2ⁿ - 2*3ⁿ) = 0 2ⁿ - 3ⁿ = 0 , 2ⁿ - 2*3ⁿ = 0 Case 1 : 2ⁿ - 3ⁿ = 0 2ⁿ = 3ⁿ log2ⁿ = log3ⁿ log2ⁿ - log3ⁿ = 0 nlog2 - nlog3 = 0 n(log2 - log3) = 0 ∴ n = 0 Case 2 : 2ⁿ - 2*3ⁿ = 0 2ⁿ = 2*3ⁿ log2ⁿ = log(2*3ⁿ) nlog2 = log2 + nlog3 nlog2 - nlog3 = log2 n(log2 - log3) = log2 ∴ n = log2/(log2 - log3)

2022(2)^2 ➖ (x)^2 +(2022^{2+2 ➖ }+{x+x ➖}= 2022^{4 ➖ x^2}+2022^{4+x^2}=2022^{x^0+x^0 ➖ x^0 +x^0 ➖}+2022^{4+x^2}=2022^{x^1+x^1}+2022^4x^2=2022^x^2+8088x^2={4044+8088x^2}=12.132x^2 1^1.1^1^1^x^2 1x^2 (x ➖ 2x+1). (2022)^2=40484 2^2^02^2^2^3^2^2 1^10.1^1^1^1^1^1^1 1^2^5 1^2^1 2^1(x ➖ 2x+1).

{4 ➖ 6}=2 (x ➖ 2x+2). {36 ➖ 81} =45 3^15 23^3^5 1^3^1 3^1(x ➖ 3x+1).

الحل بطريقة القسمة المتكررة اسهل بكثير

Go for 2022^2(x +1/x) = 2.2022^2 ( x +1/x) = 2 (√x) ^2 +(1/√x) ^2 - 2 x. 1/x = 0 (√x - 1/√x) ^2 = 0 x = 1

2022²-ⁿ + 2022²+ⁿ = 2(2022)² 2022²(2022-ⁿ + 2022+ⁿ) = 2(2022)² (2022-ⁿ + 2022+ⁿ) = 2 2022²ⁿ - 2*2022ⁿ + 1 = 0 (2022ⁿ - 1)² = 0 2022ⁿ = 1 ∴ n = 0

On squaring B/S 4^x - 2 6^x + 9^x = 6^x - 9^x 4^x - 3.6^x + 2 .9^x = 0 devide it by 4^x B/S 1 - 3(3/2) ^x + 2.(3/2) ^2 x = 0 Put (3/2) ^x = p 2 p^2 - 3 p + 1= 0 Solve the quadratic eqn. p =( 3+ -√9 - 8 ) /4 p = 1& 1/2 Recall p= (3/2) ^x = 1 , x = 0 (3/2) ^x = 1/2, take log x = log( 1/2)/(log 3/2) & 0

umm i got answer in 2 mins by factorising rhs. am i doing something wrong?

x^4 < 840 => x < sqrt(sqrt(840)) < sqrt(29) < 6 and 840 is divisible by 5. So only x=1, x=2, x=3 or x=4 need to be checked. (x=5: x is less than 6 as requested, but 6 * 7 * 8 * 9 is not divisible by 5) x=4: 5 * 6 * 7 * 8 = 1680 - no x=3: 4 * 5 * 6 7 = 840 - yes (here we can stop, because for lower x the result will be less than 840) x=2: 3 * 4 * 5 * 6 = 360 - no x=1: 2 * 3 * 4 * 5 = 120 - no (x=0: 1 * 2 * 3 * 4 = 24 - no - not divisible by 5)

840=2*2*2*3*5*7 = 4*5*6*7 Now (x +4)!/x! = 4*5*6*7= [1*2*3*(4*5*6*7)]/(1*2*3) =7!/3! It is clearly seen that x =3

a⁴ + (1/a⁴) = 47 (a⁸ + 1)/a⁴ = 47 a⁸ + 1 = 47a⁴ a⁸ - 47a⁴ + 1 = 0 Δ = (- 47)² - 4 = 2205 = 5 * 441 = 5 * 21² a⁴ = (47 ± 21√5)/2 → given: a > 0 → a⁴ > 0 a⁴ = (47 + 21√5)/2 a⁴ = (94 + 42√5)/4 a⁴ = (376 + 168√5)/16 Let's try tio find a number n = (x + y√5) such as its square is a⁴ (x + y√5)² = x² + 2xy√5 + 5y² (x + y√5)² = x² + 5y² + 2xy√5 → (376 + 168√5) 2xy√5 = 168√5 → 2xy = 168 → xy = 84 → y = 84/x x² + 5y² = 376 x² + 5.(84/x)² = 376 (x⁴ + 35280)/x² = 376 x⁴ + 35280 = 376x² x⁴ - 376x² + 35280 = 0 Δ = (- 376)² - (4 * 35280) = 256 = 16² x² = (376 ± 16)/2 x² = 188 ± 8 First case: x² = 180 → x = ± √180 = ± 6√5 Second case: x² = 196 → x = ± 14 We keep only the more convenient solution: x = 14 Recall: y = 84/x → y = 84/14 = 6 Recall: n = (x + y√5) = 14 + 6√5 Restart a⁴ = (376 + 168√5)/16 a² = (14 + 6√5)/4 Let's try tio find a number m = (x + y√5) such as its square is a² (x + y√5)² = x² + 2xy√5 + 5y² (x + y√5)² = x² + 5y² + 2xy√5 → (14 + 6√5) 2xy√5 = 6√5 → 2xy = 6 → xy = 3 → y = 3/x x² + 5y² = 14 x² + 5.(3/x)² = 14 (x⁴ + 45)/x² = 14 x⁴ + 45 = 14x² x⁴ - 14x² + 45 = 0 Δ = (- 14)² - (4 * 45) = 16 = 4² x² = (14 ± 4)/2 x² = 7 ± 2 First case: x² = 9 → x = ± 3 Second case: x² = 5 → x = ± √5 We keep only the more convenient solution: x = 3 Recall: y = 3/x → y = 3/3 = 1 Recall: m = (x + y√5) = 3 + √5 Restart a² = (14 + 6√5)/4 a = ± (3 + √5)/2 → given: a > 0 a = (3 + √5)/2 1/a = 2/(3 + √5) 1/a = 2.(3 - √5)/[(3 + √5).(3 - √5)] 1/a = 2.(3 - √5)/[9 - 5] 1/a = 2.(3 - √5)/4 1/a = (3 - √5)/2 Expression a + (1/a) = [(3 + √5)/2] + [(3 - √5)/2] a + (1/a) = [(3 + √5) + (3 - √5)]/2 a + (1/a) = 6/2 a + (1/a) = 3

Time consuming substitution 3 m - 4 = x would have been a better choice.

X=2......May be ^=read as to the power *=read as square root Let R=4+*15 A=4-*15 RA=(4+*15)(4-*16) =4^2-(*15)^2 =16-15=1 So, RA=1 A=1/R....... Eqn1 Let R^x=t As per question t+(1/t)=62 So, (t^2+1)/t =62 t^2+1=62t t^2-62t+1=0 Here a=1,b=(-62),c=1 D=b^2-4ac =(-62)^2 -{4×1×1) =3844-4=3840 *D=*(3840) =(*256)×(*15) =16.*15 So, t={-(-62)±16.*15}/2 =(62+16.*15)/2 =2(31+8.*15)/2 =31+8.*15 =4^2+(*15)^2+(2×4×*15) =(4+*15)^2 =R^2 So, t=R^2 R^x=R^2...(t=R^x) So, X=2 We can also apply logarithmic method...... R^x=R^2 Take log logR^x=logR^2 X. logR=2.logR X=2.logR/logR X=2

{a^4+a^4 ➖ }+{1+1 ➖ }/{a^4 +a^4 ➖ }={a^8+2}/a^8=2a^8/a^8=2a^1 (a ➖ 2a+1).{a+a ➖ }+{1+1 ➖ }/{a+a ➖ }={a^2+2}/a^2=2a^2/a^2=2a^1 (a ➖ 2a+1).

Add 2 & take square root twice. a + 1/a = 3

what is x^p where p=7777 in exponent form we have x=exp(iπ/3) consider p=7777=7776+1 the digit sum of 7776 is 27 which is a multiple of 3 but 7776 is even so it is a multiple of 6 hence p =6n+1 x^p = x. x^6n but x=exp(iπ/3) so x^6n =exp(2nπi)=1 so x^p=x so the answer is x or (1+isqrt3)/2 Does nobody learn the argand diagram any more.

z = (1 + i√3)/2 ← this is a complex number The modulus of z is: m = (1/2).√[(1)² + (√3)²] = (1/2).√[1 + 3] = (1/2).√4 = 1 The modulus of z⁷⁷⁷⁷ will be: M = m⁷⁷⁷⁷ = 1⁷⁷⁷⁷ = 1 The modulus of z is β sush as: tan(β) = (√3)/1 = √3 → β = π/3 The modulus of z⁷⁷⁷⁷ will be: λ = (β * 7777) = 7777 * (π/3) = (7777π)/3 = (7776π + π)/3 = (7776π/3) + (π/3) = 2592π + (π/3) λ = 2592π + (π/3) λ = (1296 * 2π) + (π/3) → but adding an angle of 2π, you can get the same point λ = π/3 z⁷⁷⁷⁷ = M.[cos(λ) + i.sin(λ)] z⁷⁷⁷⁷ = 1.[cos(π/3) + i.sin(π/3)] z⁷⁷⁷⁷ = (1/2) + i.[(√3)/2] z⁷⁷⁷⁷ = (1 + i√3)/2 [(1 + i√3)/2]⁷⁷⁷⁷ = (1 + i√3)/2

Gp formula a(rpowern-1/r-1 =1(27power6-1/27-1

(a^2+1/a^2)^2=a^4+1/a^4+2=47+2=49; (a^2+1/a^2)=7 (a+1/a)^2=a^2+1/a^2+2=7+2=9; (a+1/a)=3

On factorisation of 840 it gives four continued factors. They are 4 × 5 × 6 × 7= 840 (x+1) (x + 2) (x+3) (x +4) =840 (x+1) (x+2) (x+3) (x+4) = (3+1) (3+2) (3+3) (3+4) implies x = 3

We have a^x + a^(-x) = 2.cosh(x), so here cosh(a) = 1000/2 = 500. As cosh(2.a) = 2.((cosh(a))^2)-1, we have cosh(2.a) = 2.(500^2) -1 or cosh(2.a) = 499999, and finally a^(2.a) + a^(-2.a) = 2.cosh(2.a) = 2.499999 = 999998. Simpler: As (X^2) + ((1/X)^2) = ((X + (1/X))^2) -2, so here with X = a^1000 we have a^2000 + a^(-2000) = (((a^1000) + a^(-1000))^2 -2 = (1000^2) - 2 = 999998

(x ➖ 4x+4)/x (x ➖ 2x+2)(x ➖ 2x+2)./x (x ➖ 1x+1) (x ➖ 2x+1)/x (x ➖ 2x+1).

(1+3i/2)^3^4^3^4^3^4^3^4 (1+1i/1)^1^2^2^1^2^2^1^2^2^3^2^2 (i/)^1^1^1^1^1^1^3^1^2 (i/)3^2.(x ➖ 3ix+2).

👍 (x+4)(x+3)(x+2)(x+1) = 840 let x = y - 5/2 (y +3/2)(y+1/2)(y-1/2)(y - 3/2) = 840 (y^2 - 9/4)(y^2 - 1/4) = 840 y^4 - 5y^2/2+9/16 = 840 (y^2 - 5/4)^2 = 841 y^2 = 29+5/4 y^2 = 121/4 y = 11/2 x = y - 5/2 = 3

{(1 + √3i)/2}⁷⁷⁷⁷ = ? {(1 + √3i)/2}² = (1 + √3i)²/4 = (1 + 2√3i - 3)/4 = (- 2 + 2√3i)/4 = (- 1 + √3i)/2 {(1 + √3i)/2}³ = (1 + √3i)³/8 = {1 - 3√3i + 3√3i(1 + √3i)}/8 = {1 - 3√3i + 3√3i - 9)}/8 = - 8/8 = - 1 Let, x = (1 + √3i)/2 , {(1 + √3i)/2}⁷⁷⁷⁷ = k x² = (- 1 + √3i)/2 x³ = - 1 k = x⁷⁷⁷⁷ = x⁷⁷⁷⁶+¹ = x*x⁷⁷⁷⁶ = x*(x⁶)¹²⁹⁶ = x*{(x³)²}¹²⁹⁶ <--- x³ = - 1 = x*{(- 1)²}¹²⁹⁶ = x*1¹²⁹⁶ = x Recall, x = (1 + √3i)/2 ∴ k = (1 + √3i)/2

there is no condition for x, so i think about the real solution is 3 & - 8. (x + 4)!/x! = 840 x!(x + 1)(x + 2)(x + 3)(x + 4)/x! = 840 (x + 1)(x + 2)(x + 3)(x + 4) = 840 (x + 1)(x + 2)(x + 3)(x + 4) = 4*5*6*7 & (x + 1)(x + 2)(x + 3)(x + 4) = (- 7)*(- 6)*(- 5)*(- 4) x + 1 = 4 & x + 1 = - 7 ∴ x = 3 , x = - 8 ∴ eq. must have a factor as '3' & '- 8' (x + 1)(x + 4)(x + 2)(x + 3) = 840 (x² + 5x + 4)(x² + 5x + 6) = 840 (x² + 5x + 4){(x² + 5x + 4) + 2} = 840 (x² + 5x + 4)² + 2(x² + 5x + 4) = 840 x⁴ + 25x² + 16 + 2(5x³ + 20x + 4x²) + 2(x² + 5x + 4) = 840 x⁴ + 10x³ + 35x² + 50x - 816 = 0 x⁴ - 81 + 10x³ - 270 + 35x² - 315 + 50x - 150 = 0 (x⁴ - 3⁴) + 10(x³ - 3³) + 35(x² - 3²) + 50(x - 3) = 0 (x² + 3²)(x + 3)(x - 3) + 10(x - 3)(x² + 3x + 3²) + 35(x + 3)(x - 3) + 50(x - 3) = 0 (x - 3){(x² + 9)(x + 3) + 10(x² + 3x + 9) + 35(x + 3) + 50} = 0 (x² + 9)(x + 3) + 10(x² + 3x + 9) + 35(x + 3) + 50 = 0 x³ + 3x² + 9x + 27 + 10x² + 30x + 90 + 35x + 105 + 50 = 0 x³ + 13x² + 74x + 272 = 0 (x³ + 512) + (13x² + 208x + 832) - (134x + 1072) = 0 (x³ + 8³) + 13(x² + 16x + 8²) - 134(x + 8) = 0 (x + 8)(x² - 8x + 8²) + 13(x + 8)² - 134(x + 8) = 0 (x + 8){(x² - 8x + 8²) + 13(x + 8) - 134} = 0 (x + 8)(x² - 8x + 64 + 13x + 104 - 134) = 0 (x + 8)(x² + 5x + 34) = 0 ∴ (x - 3)(x + 8)(x² + 5x + 34) = 0 x² + 5x + 34 = 0 D = 5² - 4*1* 34 < 0 rejected ∴ (x - 3)(x + 8) = 0 ∴ x = 3 , x = - 8

We may take a brief logical approach please. The LHS is a number (840) expressed in ratio of two Factorials. The factorial as the Numerator is greater than the factorial as the Denominator Now 6!= 720 As the N/D is greater than 720 we may say that numerator will be a factorial greater than 6! So just take the Numerator =7! = (x +4)!=5040 Here x =3 So Denominator will be x! =3! Now 7!/3! =5040/6=840 Hence x =3 is the required answer.

बीच में साइन ठीक करें

(x^9 + x^8 + x^7)/(x^10 + x^8 + x^6) = 15/45 [x^8(x + 1 + 1/x)]/[x^8(x² + 1 + 1/x²)] = 1/3 (x + 1 + 1/x)/(x² + 1 + 1/x²) = 1/3 let t = x + 1/x, t² = x² + 1/x² + 2, x² + 1/x² = t² - 2 (x + 1 + 1/x)/(x² + 1 + 1/x²) = 1/3 (t + 1)/(t² - 2 + 1) = 1/3 (t + 1)/(t² - 1) = 1/3 (t + 1)/[(t + 1)(t-1)] = 1/3 1/(t - 1) = 1/3 t - 1 = 3, t = 4 ∴ x + 1/x = 4 x² - 4x + 1 = 0, x = 2±√3

=>(×+4)(×+3)(×+2)(×+1)=840 =5(4)(3)(2)7=7.6.5.4 =>×+1=4&×=3

elevando al quadrato la prima espressione e il risultato si ottiene: 1000^2 - 2 cioè 999998

elevando al quadrato la prima espressione e il risultato si ottiene: 1000^2 - 2 cioè 999998

Duh, where am I? I just fainted.

Solution by insight (a+b)^2+(a-b)^2= 2(a^2+b^2)= 2(16+15)=62 x=2 And. a+b=1/(a-b) x=-2 is also an answer

Be f: x ---> (4 + sqrt(15))^x + (4 - sqrt(15))^x. f(x) = (4 + sqrt(15))^x + (4 + sqrt(15))^(-x) = exp(x.ln(4 + sqrt(15))) + exp(-x.ln(4 + sqrt(15))) = 2.cosh(x.ln(4 + sqrt(15))) f verifies f(x) = f(-x) for any real x, and if we limit f at R+ then it is a bijection from R+ to [2, + infinity[ As 65 is in [2, +infinity], the equation f(x) = 65 has an unique solution x0 on R+ and an unique solution -x0 on R- As x0 = 2 is evident solution we then have that the given equation has two solutions and only two: 2 and -2.

If you check the absolute value of x, it turns out to be 1. Also x can be written as e^(iπ/6) . Then taking any power is much easier.

Can be substituted (1 +√3i) = p Transpose and square it giving you p^2 -p +1=0 Multiply it with (p+1) B/S Give you P^3 + 1= 0 P^3 = - 1 (1) square it B/S P^6 = 1 ...... (2) now 7777 = 1296×6+1, as such P^7777 = (P^6) ^1296×P = 1×(1+√3i) /2

YOUR CALCULATION IS WRONG, THERE IS NO SUBSTRACTION..

Nice solution and good explanation

Sorry, typo. Let 27 = a. Let answer value = S. (a-1)S = a^6 -1. Therefore, S = (a^6 - 1) / (a - 1) = (27^6 - 1) / (27 - 1) = 14,900,788. So simple! Do not show the stupid method.

❤ also cube root (√5+2) - cube root (√5 - 2) = 1

a¹⁰⁰⁰ + a-¹⁰⁰⁰ = 1000 a²⁰⁰⁰ + a-²⁰⁰⁰ = ? a¹⁰⁰⁰ + a-¹⁰⁰⁰ = 1000 a¹⁰⁰⁰ + 1/a¹⁰⁰⁰ = 1000 Let, a²⁰⁰⁰ + a-²⁰⁰⁰ = k k = a²⁰⁰⁰ + a-²⁰⁰⁰ = (a¹⁰⁰⁰)² + (1/a¹⁰⁰⁰)² = (a¹⁰⁰⁰ + 1/a¹⁰⁰⁰)² - 2 = (1,000)² - 2 = 1,000,000 - 2 = 999,998

Very very very slow explanation boring