Відео

after like 6 hrs of constantly thinking, i kinda get how the algorithm work now. basically, if we have 2 natural numbers a and b, we can write them in the form: a = C*ua b = C*ub where C is the least common divisor and u's are the unique divisors the goal here is to reduce u to 1. we can do that by constantly taking remainder division which preserves C if we write a = nb*b+R and substitute a and b in, you will see the remainder always contains C R = C(ua - nb*ub) we will know whether either of the u's is 1 when the remainder is 0 ua = ua - nb*ub makes ua < ub since ua < (nb + 1)*ub (nb is the greatest number of b contained in a, aka a/b) so everytime we take remainder, the larger/smaller side switches making u reduce constantly while staying positive there will NEVER be such C*2*3 and C*2 case since that makes C*2 the gcd, wich contradicts with the claim that C is the gcd

This + thinking gives refreshing perspective on what the heck my lecturer been trying to get to me. It's always the fact that you need to process raw information first, before understanding it normally.

The quotes of the beauty of math outside practical applications sum up math programs I've written. Haven't contributed much to my career with it...

this is the best explanation i ever have❣❣

Whaaaaaaaaaaaat?! Wow! thank you so much for this visual example, it's so good and can be configured for an activity on one of my classes!

I love you so mucchhh. This makes Visually tremendously more sense…

the best explanation, much much easier but the problem is lecture just want exactly like how they explain

Thank you very much ❤❤❤

Wow, this video is simply amazing, not only do you help us visualize the algorithm but you also make it intuitive to the point where you can derive it yourself. Thank you so much! I will be sure to check your videos out for future concepts!

SO UNDERRATED

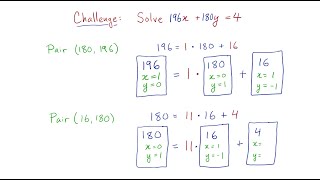
At 4:53 you write: 180=11*16+4 but correct would be +20 instead of +4 and then you get 20=16+4 followed by 16=4*4+0 and gcd=4

7:14 I said "Ohhhh" out loud as now I think I get it.Thank you

The best explanation on this topic

Wouldn't it be easier to factor the 10 million numbers and publish a table lol.

Great video that i watch every once in a while.

damnnnnn bro! 🤯🤯

Best explaination ever made for this topic by just one joing lines of a traingle you explained the smallest detail. Thank you very much for this it was so much helpful.

почему нет руского перевода??? правильно ютуб в России забанили поделом

In terms of an orchid problem, I like Phi, rhe golden ratio instead if pi. Since it's "the most irrational number" meaning there is no good approximations. This approach or even the surreal numbers, allow for ording all the irrationals. so doesnt that allow a mapping from rationals to irrationals and showing that they have the same cardinality? Ruining the second diagonal argument? Instead of numebrs, you can also do this with powersets over sll rationals.

Florence Union

thank you for the awesome content

i truly wish i saw this video first years ago. how many times i have given up, confused on the notations, given its apparent inconsistency in use. now that you pointed out that it is a side note, it is so clear now. thank you. just wish i saw this years ago.

Its been a month since I graduated engineering, and now is the day when I truly understand this algorithm

If you just have L/R options, would there be a significant difference between using fairy* subdivisions instead of binary ones? Also, the fractions you put on the grid don't quite make sense to me. (1,1) is further from the origin than (0,1) and (1,0), so it seems like it should represent 1/2 instead, since it looks smaller, with (1,0) representing 1, (1,2) and (2/1) representing 1/3 and 2/3, (1,3) and (3/1) representing 1/4 and 3/4, and so on. *[sic is what you get for being called Farey and not spelling it out :P]

Williams Ronald White Frank Thomas Anna

UA-cam has a lot of trash on it - and then it has things like this. I think this is a serious contender for the best STEM-related video I've ever seen.

Here's how to calculate the numbers used in the sequence of a continued fraction. You take the number, - the biggest whole number you can find, then flip the remainder as a fractional addition, and then repeat. ie: 3.14 - 3 = .14, 1/.14= 7... 1/... = 15... 1/...= 1... 1/... = etc where 3,7,15,1 would be the 'address' instead of 3,1,4,...(base 10 address) Loved the video, and now that i understand the process to generate continued fractions, I agree with you, it's actually VERY easy to calculate the continued fraction. It only requires simple subtraction and division, where as calcuating base 10 of a number also requires simple subtraction and division. Now getting the actual 'value' back from a continued fraction, is a lot more involved (every address you go, requires another division and addition (and the addition involves multiplication), where as with any normal base address it only requires 1 simple multiplication per address, so indexing in is much easier than indexing out, which means numberical bases are here to stay, like you said, but its still quite clever and I loved thinking through the arguments and watching the visualization. Edit: I did some more thinking about this, and actually you need the base 10 system to write out the continued fraction in the first place. So this is an index, of an index. If we wrote all the numbers in base 2, the continued fraction would look way different. Doesn't change much, but I did overlook that, this isn't a 'better' address divorced of the base 10 address, it's an even more specific, base 10 address.

honestly, this was so cool

Thanks for your explanation! Just a quick correction, in your example, the number of dots is 57 instead of 54. gcd(21, 57) = 3 is still true tho.

i watched your video a few months ago and ive been thinking about it constantly, its changed the way i view number! super thanks!

Love you

I am interested in understanding how things work rather than memorization, and in less than a minute of the video, I knew it was special. Content such is this is absolutely vital. Thanks.

Beautiful

This is brilliant. Please continue to make more such videos. This is how science and math must be seen.

At first, I didn't quite grasp why would the GCD remain same after we delete the smaller number from larger one (B-A). But it made sense this way: Hint: We are deleting pile A from pile B and then ask what's the new GCD of leftover pile B and the pile A? Well, just remember, the deletion is also made of new GCD as we just deleted pile A- hence the whole pile B and pile A have a new GCD ;) contradiction ! Explanation: GCD is basically the largest chunk of stones that will divide both piles in some number of parts, say- xa and xb. So, pile A has xa number of GCDs and pile B has xb number of GCDs (largest chunks common for both). => A = g . xa and B = g . xb (Imagine them as bigger balls that make up the pile) Now, we remove just one copy of pile A from B. This means: => B - A = g . xb - g . xa For a moment, let's assume, the common chunk size of A and B-A, could maybe get bigger after deletion- to say g' (read: g dash) => B - A = g' . x' and A = g' . xa' This means, the leftover of pile B is made of g' size chunks with count as x' and pile A is made of g' size chunks with count as xa'. But, here's the catch: the deleted pile A from pile B must also be made of g' size chunks with count as xa'. That means: => deleted pile A + left over pile B = the original pile B => g' . xa' + g' . x' = pile B => g' (xa' + x') = pile B So, the pile B is made of g' size chunks AND pile A is also made of g' size chunks! A common divisor for A and B! What's the largest common divisor for A and B? => The GCD(A, B) = g Hence, g' = g, the original GCD of A and B!

WOW. You explain stuff in such an intuitive manner

This should be first hit for Euclidean algorithm

our explanations are similar except I cut the box Into Identical sections

Excellent video.

A new classic here! I've had this video in my Downloads for some time.

This was mind-blowing to watch. I'm amazed at how you could convey everything so neatly and clearly.

love it;❤

Thanks.

Weird how this video was located next to Lemmino's new video

Came here after Leminno video about Kryptos. Nice video! And the puzzle was fun, althought at first I didn't know what to do with the fact that last row is incomplete. But when you think about it, it becomes more or less obvious.

Really enjoyed this video, gave me a new reason to love maths even more! One tiny note: it should be pronounced "Dirishley".

This is fantastic, thank you!

I think this is a WILDLY helpful video. Awesome job.😎

7:25 once you dropped down into the origin my brain immediately made the connection between the inverse square law & what was being talked about previously

At 2:30 you said, “. . . like Pi as the ratio of diameter to circumference”.