Modular Arithmetic: User's Manual
Вставка
- Опубліковано 7 лют 2025
- Modular arithmetic visually! How to compute modulo n, efficiently and with intuition. We rely heavily on visual intuition.
This video is appropriate for anyone interested in modular arithmetic! It could be used in high school, for an introduction to proof course, for undergraduate mathematics or computer science majors, or for the mathematically inclined, especially those interested in cryptography or number theory.
This is part of a series on modular arithmetic with visualization: • Modular Arithmetic Vis...
For associated materials:
proofofconcept...


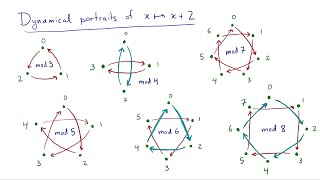






i truly wish i saw this video first years ago. how many times i have given up, confused on the notations, given its apparent inconsistency in use. now that you pointed out that it is a side note, it is so clear now. thank you. just wish i saw this years ago.
bro why you are so good at this? we need you in competitive programming community please teach us more of this way of thinking about numbers.
I totally just shared this with someone I was teaching about different counting bases today (octal, hexadecimal, and binary, in particular, because it's for the purpose of helping her with computer programming, but I aimed to teach it more generally, too). I hope it helps. It definitely seems, err, _congruent_ to the intended learning goals. ;)
Could be helpful to introduce the common nomenclature for the "shadows", as members of residue classes modulo N. Great series!
Good point!
For the 17^3 * 8 exercise around ~7:50 mark, I first factorized 8 into 2^3 then simply added 17 + 2 at power 3 to get 19 - which is also in the "4" ray.
Hey, I have got one question. I have tried it the same way, but I thought because of the exponent rules it would be the same as (2×3)^8. Why doesn't it work like that in this instance?
I'm stumped at 7:15. We decide that we can replace a 16 with a 1 in an expression. However, we've been saying throughout that we shouldn't use the equals sign but should use a congruent sign instead. I'm used to substituting equivalent expressions to simplify larger expressions but I'm having a hard time accepting that we can substitute congruent expressions. Why can we do that?
I'm starting to convince myself because I can see how substitution works with addition and it seems like it would be logical to extend that to multiplication and then to powers but I'm still having trouble visualizing the turns of the clock for those operations.
Ah! I should have kept watching. The how and why is in the next video :)
@@minesfeaver I love watching the progression of comments here, it made my day! This is exactly what I was hoping would happen: as you see it work, you can't help but feel it's magic and it needs an explanation. It does need an explanation! I hope the next video answers the "why" for you.
This is indeed a fun sequence of comments. :)
this is perfect. thanks!
It was great, easy and beneficial teaching 👌👌
This is amazing !!!!!!