JAPAN || A Nice Olympiads Trick
Вставка
- Опубліковано 27 січ 2025
- Looking to master tricky math problems like a pro? In this video, I break down a classic Olympiad-style problem.
Learn the quick and clever factoring trick to simplify massive exponents in seconds. Perfect for math enthusiasts, competitive exam prep, and anyone looking to level up their problem-solving skills!
Topics Covered:
Exponent simplification tricks
Factorization for large numbers
Olympiad-level problem-solving tips
Don’t miss this essential trick that makes math so much easier!
#maths


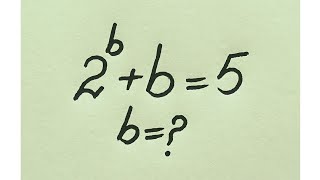






3n=Vn => 9n²=n
9n²-n=0 => n(9n-1)=0
n=0; n=1/9.
2^√n=8^n
2^√n=2^3n
√n=3n
1=3√n
1÷3=√n
Squaring on both sides
1÷9=n
√n.log2 = n.log8
We know log 2 and log 8
Then forms and equation on squaring both sides, then solve it.
Since 8^n=(2^3)^n=2^(3*n), we get:
2^sqrt(n)=2^(3*n) | equal bases and base is neither 1 nor 0, so this identity requires also equal exponents
sqrt(n)=3*n
sqrt(n)=3*sqrt(n)*sqrt(n)
3*sqrt(n)*sqrt(n)-sqrt(n)=0
(3*sqrt(n)-1)*sqrt(n)=0
3*sqrt(n)-1=0 or sqrt(n)=0
sqrt(n)=1/3 or n=0
n=1/9 or n=0
1.22
a^n=a^m does not necessarily require n=m. That is only the case, if a is neither 1 nor 0 (which is the case in this excercise since 2 is different from 1 and different from 0, but it should be mentioned in the video).
1:39
Why do you square both sides here?squaring an equation may produce additinal results, which is unnecessary at that moment. You may rewrite n on the right side as sqrt(n)*sqrt(n), bring all to one side and take the common factor sqrt(n) out of the sum. With this method, you have not the risk of producing additional erroneous results. I think, ypu should avoid squaring an equation until it is absolutely necessary. When you square an equation, you have ro check every found solution, because it may be an errneous solution. i did *not* dquare the equation, i have not made any transformation, that may lead to errnous solution, so i don#t need the check in my solution.
7.27
You don't have to rewrite 2^(1/3) to see, that the equation is fullfilled. Iz is obvious that 2^(1/3)=2^(1/3), since the terms on both sides are already equal.
By observing the equation we get
n = 0 at first sight but if n ≠ 0 then,
2^√n = 8^n
2^√n = 2^3n
√n = 3n
Squaring both sides
n = 9n²
Divide both sides by n
n/n = 9n²/n
1 = 9n
1/9 = n
Also n=0. You cannot divide by n because it could be zero. You subtract n from the other side and factor out n, then there are two roots, n = 0 and n= 1/9.
There is a second solution ... What about n=0?
@@bakrantz Is it alright now or am I violating any rules?
√n = m
2^m = 8^(m^2) = 2^(3m^2)
m = 3m^2
m(3m - 1) = 0
m = 0, 1/3
n = 0, 1/√3
Let’s divide 2^n=(8)^n by 2^n we get:
(8/2)^n=1
4^n=1
n.Log4=Log1 =0
n.Log4 =0 n=0
2^(3)=8^(1)=8 2^3 1^1^2 1^2 ( n ➖ 2n+1).
(2)^(n^1/2)=2^(3n)
n^(1/2)(log2)=3n.(log2)
n^1/2=3n=3n^1/2.n^1/2
1=3n^1/2
n^1/2=1/3
n=1/9
What about the solution n=0?
@@juergenilse3259We don’t need to add this bc that would be trivial
@ n=0 is a solution and should be mentioned for a complete solution. You have divided by n^(1/2) without making shure, that n^(1/2) is different from zero, which is a mistake. Your solution is *not* correct, even if you detected 1 of the 2 solutions.
@ go back and review your lessons on exponents.
n^(1/2) is simply square root of n
that I can also write as n^(0.5) that you should not confuse with a division but even when you divide 0 by any number different from 0 you get 0
Also note 2^(n^1/2) isn’t the same as 2/n
@@juergenilse3259 in the problem it is implied that n=/= 0 bc this is trivial
N=0, N=(1/9)
rtn=3n
3rtn=1
rtn=1/3
n=1/9
2^n=(2^3)^n
2^n=(2^n)(2^n)(2^n)
1=(2^n)(2^n)=2^2n
Lg1=2nLg2
0=nLg4 n=0
2 root n = 8 ^n
2 root 9 = 8^3
N= root 9~(3)
2^3 = 8 ❤❤😢
2^√n=8^n
2^√n=(2^3)^n
2^√n=2^3n
√n=3n
n=9n^2
0=9n^2-n
0=n^2-n/9
n=1/18±√(1/324)
n1=1/18+1/18=1/9
n2=1/18-1/18=0
Red comments , 1/9 is true result.....from initial equation following future to 2 in 3n is equal to 2 in square root from b. Further 3n is equal to square root from n , further final answer...ありがとうございます。タスクは興味深いです. ..
log ... = log ... ==> n ^(1/2) =3n ==>n =9n^2
If n=0, 0= 0 OK
In not 1=9n and n=1/9 OK
Too many trivial and redundant steps. Keep ot short. Dr. Ajit Thakur (USA).
The reason is to teach not just show the answer. Steps are important. Dr. Ivo, España.
@@GIFPES i understand the reason, but the check would not be necessary, if we avoid squaring the equation. Squaring the equation is the only transformation, that may introduce additional errneous solutions, so if we rewrite n as sqrt(n)^2, we can avoid sqaring the equation and get the 2 possibilities sqrt(n)=0 and sqrt(n)=1/3, which leads to the same result, because it is obvious, that 0 is the only real number, whose square root is 0 and 1/9 is the only real number, whose square root is 1/3.
maybe, it would be a clever idea, to mention that in the video.
@@juergenilse3259 yes for extraneous elements are prevented to appear.
@ You only need to check, if you apply transformation, that may add extranous solutions. The only such transdormation done in the video is squaring the equation. I found a solution without squaring the equation, so in my solution, the check is unnecessary (but may be done, if you want9, For the solution in the video, the check is necessary to make shure, that all found values are really solutions.
So rewriting n to sqrt(n)^2 instead of squaring the equation is the more elegant solution, because it may make the check unnecessary.
But you are not allowed to divide by sqrt(n) without making shure, that sqrt(n) is not equal to 0. The solution is to take the common factor sqrt(n) out of the sum and use the rule, that a product is zero if and only if at least one factor is zero. With taking out the common factor sqrt(n) out of the sum, you don't need to divide by a term, that might be 0.
@juergenilse3259 indeed, 0 cannot be a solution for it does not apply as log base. 1/9 is the only one solution. Zero is extraneous.
1/9
Gringo lo hice de memoria n=0