A Nice Algebra Challenge | Can You Solve? | Exponential Equations
Вставка
- Опубліковано 10 лют 2025
- A Nice Algebra Challenge | Can You Solve? | Exponential Equations
Welcome to another interesting algebra challenge! In this video, we'll be solving an exciting exponential equation. Whether you're preparing for a Math Olympiad or just love a math puzzle, this problem is perfect for you. Grab your pencil and paper, and let's see if you can solve this exponential challenge!
📌 Don't forget to like, comment, and subscribe for more math challenges and tutorials!
🔔 Hit the bell icon to get notified whenever I post new content!
Recommended Videos:
• Solving a Nice Exponen...
• An Engaging Algebra Si...
• A Nice Radical Math Pr...
• A Nice Radical Equatio...
#mathchallenge #exponentialequations #algebra #matholympiad #problemsolving #learnmaths #education #algebrachallenge
Don't forget to like this video if you found it helpful, subscribe to our channel for more Olympiad-focused content, and ring the bell to stay updated on our latest math-solving sessions.
Thank You for Watching!!



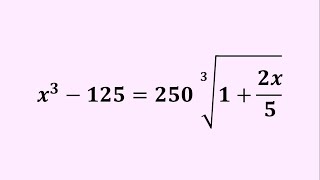





x=2.585
Let 2^x=a. Then, a^3+a=222. The only real solution is a=6. So, 2^x=6 which means x= (ln6)/(ln2) =1 + (ln3)/(ln2).
yes or more simply, x=log_2(6) which I did in my head in less than a minute.
If complex solutions are required it should say so in the question. x∈C is easy enough to write
a quick answer x∈C
y=2^x, y^3+y=222
y^3+y-(6*37)=0
(y-6)(y^2+6y+37)=0
y=6
y=(-6+-√(36-4*37))/2
y=(-6+-√-112)/2
y=-3+-i√28
solutions
y=6
y=-3+2i√7
y= -3-2i√7
x=log_2(y)
ln2.x=lnr.ln(e^iθ)=±lnr.iθ= ±iθlnr
r=√(9+28)=√37
θ=arctan(28/9)
x=±i arctan(28/9).ln(√37)
2^χ+(2^χ)^3-222=0 2^χ>0 2^χ=α>0
α^3+α-222=0 α^3+α-222=(α-6)(α^2+6α+37)=0
α=6 ή α=-3+-2i(7)^(1/2)
2^χ=6 ...χ=1+log_2(3) στο συνολο R
{111+27.6}=38.7 111^27.6 55^66^18^18.7 2^3^2^3^3^3^3^3 2^3^2^3.3^4 1^1^1^1^1^1^1^1.3^2^2 1.3^1^2 3^2(x ➖ 3x+2).111^111 55^66^55^66 2^3^2^3^3^3^3^3^2^3^2^3^3^3^3^3 1^1^1^1^1^1^1^1^1^1^2^1^1^1^1^3 2^1^1^3 23 (x ➖ 3x+2).