Domains of holomorphy and Dolbeault cohomology
Вставка
- Опубліковано 30 вер 2024
- Domains of holomorphy can be characterized by vanishing of Dolbeault cohomology. We prove one direction of this characterization. For more detais see Gunning's "Introduction to holomorphic functions of several variables, Vol 1", Section G.
Please point out any imprecisions in the comments below.
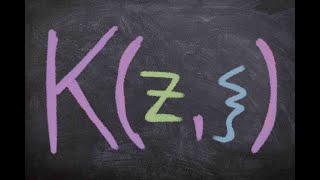




![[UA] NAVI проти G2 Esports | Blast Premier Fall Final](http://i.ytimg.com/vi/QWlIm4FGESQ/mqdefault.jpg)



At 3:08 what is $X$? Is it $\{(z_1,\dots, z_n): (z_1,\dots, z_{n-1},0)\in L\cap \Omega, z_n\in \mathbb{C}\}$? We probably need to be more careful about the cutoff then.
Thanks for noticing. X should be simply Omega here. Indeed, I should have said more about the construction of rho, but I am never really sure how much details is OK in math UA-cam videos.
@@manifoldsinmaryland How can $X$ be $\Omega$ if the section $L\cap \Omega$ is small ? e.g. take $\Omega$ to be a ball in $\mathbb{C}^2$ and let $L=\{z_n =0\}$ be a complex line that does not pass through the center of $\Omega$ but intersects $\Omega$ in a nonempty open set. Then the formula $g(z_1,\dots, z_n)= f(z_1,\dots,z_{n-1})$ does not define $g$ on all of $\Omega$, but on a proper subset.
@@debraj10 not sure what you mean. I say specifically that g is defined on a proper open subset of Omega. Then I construct the global extension using a cutoff of L cap Omega.