Japan Math Olympiad | A Very Nice Geometry Challenge
Вставка
- Опубліковано 27 чер 2024
- Japan Math Olympiad | A Very Nice Geometry Problem
MY OTHER CHANNELS
••••••••••••••••••••••••••••••••
Calculus Booster : / @calculusbooster
Math Hunter : / @mathshunter
--------------------------------------------------------------------------------
Join the channel to become a member
/ @mathbooster


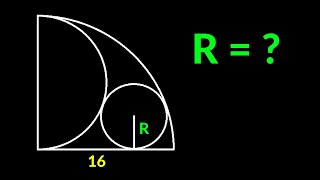






Just some analytical geometry:
1. Let A(0;0);
r= radius of the large outer semicircle;
2. equation of the circle with center Q: (x-6)^2+(y-3)^2 = 3^2; it is intersected by QC which equation is y=3 in point C;
(x-6)^2+(3-3)^2=3^2;
x-6 = 3; => x=9 => C(9;3)
3. Equation of the large outer semicircle is:
(x-r)^2+y^2=r^2;
as it passes through C(9;3):
(9-r)^2+3^2=r^2;
81-18*r+r^2+9=r^2;
90=18*r;
r=5.
4. Ared = pi*5^2/2 - pi*2^2/2 - pi*3^2/2 = 12*pi/2=6*pi sq units.
Let O be the center of the largest, outer semicircle, P be the center of the larger inner semicircle, and Q be the center of the smaller inner semicircle. Let A (left) and B (right) be the ends of the diameter of semicircle O, C (left) and D (right) be the ends of the diameter of semicircle P, and E be the remaining end of the diameter of semicircle Q. Let T be the point of tangency between the two inner semicircles, and S be the point of tangency between the circumference of semicircle P and AB. Let R be the radius of semicircle O, as the other two radii are given.
Draw PQ. When two circles are tangent to each other, their point of tangency is collinear with their centers. Thus PQ passes through T. As PT = 3 and QT = 2, PQ = 3+2 = 5. AB is tangent to semicircle P at S, so ∠ASP = 90°. As PS = 3 and PQ = 5, then ∆QSP is a 3-4-5 Pythagorean triple right triangle and QS = 4.
Draw DM, where M is the point on AB where DM is perpendicular to AB, and draw AD. By observation, AM = AQ+ QS+ SM = 2+4+3 = 9, and DM = PS = 3.
Triangle ∆AMD:
DM² + AM² = AD²
3² + 9² = AD²
AD² = 9 + 81 = 90
AD = √90 = 3√10
Draw DB. By Thales' Theorem, ∠BDA = 90°, as A and B are ends of a diameter and D is on the circumference. As ∠AMD also equals 90° and ∠DAM is common, triangles ∆AMD and ∆BDA are similar.
Triangle ∆BDA:
AB/AD = AD/AM
2R/3√10 = 3√10/9
18R = 90
R = 90/18 = 5
The red shaded area is equal to the area of semicircle O minus the areas of semicircles P and Q.
Red shaded area:
A = πR²/2 - π3²/2 - π2²/2
A = 25π/2 - 9π/2 - 4π/2 = 12π/2 = 6π sq units
CD=DM=MQ=3; PQ=2+3=5
ΔPMQ - right triangle (3/4/5) => PM=4
AD=2+4+3=9; BD=AB-AD=2R-9
ΔACB - right triangle => CD²=AD•BD
9(2R-9)=3²; 18R-81=9; 18R=90; R=5
A=½π5²-½π2²-½π3²=½π12=6π 😁
(2)^2=4 (3)^2=9 {4+9}=:13 180°PM/13=10PM.50 2^5PM.5^10 1^1PM.1^2^5 2^1 (p ➖ 2m+1)
You don't need chord theory to get X. Construct lines AC & CB. ACB is right triangle & is similar to triangle ADC. AD/DA = 3 = BD/CD.
BD = X =1. From there you have diameter AB of the large circle & the areas can be calculated.
Another easier than it looks problem and it shows that before calculating the area of a semicircle always check if the diameter is given. If not, then use two circle theorems and chord lengths.
Imagine having this on a big screen. Movie night goals!
Draw a point O on line AB (which is a diameter of the large circle) 3 units to the right of P. Draw a line from O to C. Then PQCOP is a parallelogram and AO and OC are both 5 units long, so both are radial lines and O is the center of the large circle. Then area of shaded area is half of 25*pi - 9*pi - 4*pi.
Wonderful use of parallelogram.
6:33 and how this can be proven
At first look I thought about similar triangles and probably it is not a bad idea
(To justify that we have similar triangles we have to identify inscribed agles subtended by the same arc)
Parabéns pelos excelentes vídeos e pelas ótimas soluções!
In un sistema cartesiano opportuno(O è il centro del grande cerchio),il punto C=((R-3)^2/(6-R),3)...quindi imposto l'equazione ((R-3)^4/(6-R)^2)+9=R^2...semplifico e rimane R^2-8R+15=0, dà soluzioni R=5,R=3..per cui è certamente R=5..a questo punto procedo per differenza delle aree
Real solution starts there 6:15
(2+4+3)*x = 3^2, so x = 1 and the diameter = (2 +4+ 3) + x = 10.
So the area = pi(5^2 - 3^2 - 2^2)/2 = 6pi.
Sir, I've solved the question in this way...😊
What I see on Indian math channels is way beyond of what I see on German math channels. Up to 5;05: Piece of cake. As of 5:05: Never heard of this rule. Ever. Although it is intuitively correct, German schools do not teach this rule.
My highest respect for India. Go on like this, and your kids will become engineers, who will soon take the lead on technological advance.
I am a retired electrical engineer who spent the majority of my career years in the so called Silicon Valley of California (San Jose and surrounding areas, including Cupertino, where Apple Computer has its headquarters). I worked with a number of Indian engineers, as well as engineers of other nationalities. We worked well together. There are some parts of a project where an Indian engineer would take the lead, but other parts where engineers of other nationalities took the lead. I never considered the Indians to be a threat, even if they outnumbered those of us born in the USA. Most likely, because the Indians are here, there are more engineering jobs for us natives, not fewer.
As for the "intersecting chords" theorem at 5:05, I am surprised that you weren't taught it in Germany.
My high school geometry classes focused on proofs. I find these problems far more interesting than proofs.
❤❤🎉🎉