Proof of Product Law (Limit Laws)

Proving the product law of limits rigorously with the epsilon-delta definition.
REMARKS:
If we have a function h, with domain D, where h(x) = f(x)g(x), we may evaluate its limit by decomposing this function into the product of the functions f and g, where f and g both have domain D, and limits L and M at point c respectively.
The product law tells us that the limit of h(x) (also written as (fg)(x) to emphasize the fact the function can be split into the product of two other functions) is simply LM.
Of course all of this goes without saying that we've assumed point c to be a cluster/accumulation point of the domain D. It makes no sense to talk about the limit if this condition wasn't satisfied.
This law can help us establish a whole range of results without having to go through the hassle of establishing an epsilon-delta definition all the time.

[@_Lumini_]

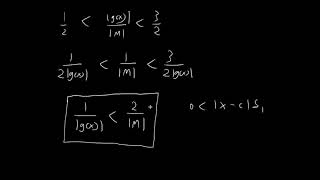
You manage to get straight to the point while clearly explaining the nessecary steps. With the added bonus of a great voice for this kind of video. Nicely done!

[@HayashiManabu]

Thanks :)

[@speedysenu4183]

Thank you ❤! Your proof was the only one I saw that actually made sense. Good job.

[@hayek2912]

Great job, thanks for your hard work, your video really helped me figuring out how to prove limit laws, I stucked at here almost a week...

[@speakingsarcasm9014]

Very nice! I managed to extend this to multi-variable context.

[@dtgiabao03]

thank you so much!

[@wasayrafaqat6838]

This was very good! tysm

[@vanitasofthebluemoon9747]

yo, this helped a lot, thanks a lot

[@dtgiabao9915]

Thank you so much

[@Nothingness1305]

Aren’t |L|/(1+|L|) and |M|/(1+|M|) both just less than one? How can they be less or equal to one?

[@joshhh___]

Since |L|/(1+|L|) is less than 1, it is less than or equal to 1, as it satisfies the less than condition.