A Factorial Perfect Square?
Вставка
- Опубліковано 1 жов 2024
- 🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
/ @sybermathshorts
/ @aplusbi
❤️ ❤️ ❤️ My Amazon Store: www.amazon.com...
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
You can find ARML books and many others here. CHECK IT OUT!!! ❤️ ❤️ ❤️
❤️ A Differential Equation | The Result Will Surprise You! • A Differential Equatio...
❤️ Crux Mathematicorum: cms.math.ca/pu...
❤️ A Problem From ARML-NYSML Math Contests: • A Problem From ARML-NY...
❤️ 1!2!...100!/m! = k^2
❤️❤️ Solving A Differential Equation: • Solving A Differential...
⭐ Join this channel to get access to perks:→ bit.ly/3cBgfR1
My merch → teespring.com/...
Follow me → / sybermath
Subscribe → www.youtube.co...
⭐ Suggest → forms.gle/A5bG...
If you need to post a picture of your solution or idea:
in...
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries
#algebra #numbertheory #geometry #calculus #counting #mathcontests #mathcompetitions
via @UA-cam @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Number Theory Problems: • Number Theory Problems
Challenging Math Problems: • Challenging Math Problems
Trigonometry Problems: • Trigonometry Problems
Diophantine Equations and Systems: • Diophantine Equations ...
Calculus: • Calculus


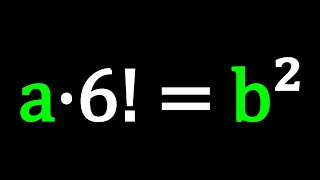






Good Morning,Sir
This problem was extremely difficult for me,how did you figure it out so easily
It's incredibly ingenious
James Wang 06-29-2024
Well one observation is 97 is a prime number and no other way to make a perfect square therefore m>=98 and only 99 seemed to fit m =99 and K =10 no other way to make a perfect square
You have yet to prove that 50! is NOT a perfect square because otherwise m can be 1.
Good. But I think you still need to prove that is the only solution. e.g. why m=60 is not a solution?
50!? Its too hard to calculate k for me
Because... I think you don't have enough experience...math is all about practice.. the more you practice the more you become good at it
Stopping anyone saying "First"
Second 🙋
You're just like them.
Stop you too.
Fair enough @@yuseifudo6075
0!th
I have GOT to redevelop my perseverance. So close!
There’s a stackexchange post asked by math-sd which proves uniqueness.
😮
Is it the only solution?
Definitely not. Let's reduce the problem to human-sized numbers. (1!2!)/m = k^2 can only be m = 2 and k = 1. (1!2!3!4!)/m = k^2. is easy enough to calculate. mk^2 = 288. In this case, m can be 2, 8, 18, 32, 72 and 288. k can be any divisor of 12. Going to 6! the numbers get cumbersome, but early on I see values for m as 3, 12, 27, 48, etc. and the ks are all divisors of 2880. So there is likely an enormous number of possible answers.
I think it is, considering the way factorials work, but I can't prove hahaha
@@Qermaq except that we are dividing by m!, so the denominator must also be a factorial. For (1!2!3!4!)/m! = k^2 the only solution is m = 2, k = 12.
I can't think of an easy way to prove that the answer in the video is unique, but I also can't see another factorial to divide by that will leave us with a perfect square.
@@lettucehelper It still remains that the set of candidates grows larger quickly. It's hard to imagine that the options won't yield more fruit
@@Qermaq "hard to believe" is not the same as "definitely not".
If we don't divide by 50!, then we can think about the following cases:
1) m is odd. Here, m! x 50! needs to be a perfect square because we have divided (m!)^2 by m!, leaving everything else as a definite perfect square except for m! x 50!, which we must explore further.
For m < 50 we are left with (m!)^2 x (m+1) x (m+2) x... 50; in other words (m+1) x (m+2) x... 50 must be a perfect square. 50 is not a perfect square (m = 49). 49 is, but 48 x 50 is not, so 48 x 49 x 50 is not (m = 47). 47 is prime, so for odd m 50 we need 51 x ... (m-1) x m to be a perfect square. 51 is not a perfect square (m = 51). 53 is prime so 51 x 52 x 53 cannot be a perfect square (m = 53), and, in fact we cannot form a perfect square for any odd m >= 53.
2) m is even. This is more complicated. m! was earlier paired with (m-1)! to give [(m-1)!]^2 x m. This then became [(m-1)!]^2 x 2 x (m/2), with the 2 being part of (2^25)^2 and m/2 being part of 50!
I hope that is clear so far.
Dividing by m! removes one of the (m-1)! factors, one of the 2s and m/2 from 50!.
This leaves [all remaining odd factorials squared] x [2^24]^2 x (m-1)! x 2 x [1x2x...(m/2 -1) x (m/2 + 1) x... 50]
so, now we need: 2(m-1)! x 1 x 2 x... (m/2 -1) x (m/2 +1) x... 50 to be a perfect square. Rewriting to form as many definte squares as possible we have:
4 x [(m/2 - 1)! x (m/2 + 1) x (m/2 + 2) x... (m-1)]^2 x m x (m+1) x... 50.
Meaning m x (m+1) x ... 50 must be a perfect square. But it cannot be. 50 is not a perfect square. 49 x 50 is not. 48 x 49 x 50 is not. 47 x 48 x 49 x 50 is not. And any m < 47 cannot be, because 47 is prime.
Unless I missed something, I think that's a rigorous enough proof to say that 50! is the only answer to the question.
hey SyberMath, can you make a video of matrices, determinants, vectors, probability & statistics of each individually?
I don't think this is a rigorous proof. They simply took it as a fact that 50!/m! cannot be a square for other values of m.
It’s not. That’s the whole point 🤪
@SyberMath I was wrong about m=100.
if m = 100, then we divide the giant numerator by 100!, which leaves 1!2!3!...99! = [(1!3!5!...97!)^2]x[2^49]x[49!]x[99!] = [(1!3!5!...97!)^2]x[(49!)^2]x[(2^24)^2]x[2 x 50 x 51 x... x 99]
which is not a perfect square.
for rigor you can start by checking number of primes from 97 and end on getting that 46
I remember solving a version of this problem years ago. Same method as in the video, which is the smart way and easily generalizable to any similar product ending at a multiple of 4.
I have seen people try to solve this by counting prime factors, like there are 57 occurrences of the prime 47 in the product of the first 100 factorials, so then whatever factorial to be removed must have an odd number of 47's within its own product. Obviously you will need a lot more than one such observation and that method scales poorly.
What are the solutions to x^3 - y! = 2024 and why?
Well, up to y = 6, x is reliably about 12. But as y gets larger x gets way smaller all of a sudden.
Why? I don't know, but I'm willing to listen. x has been through a lot. I mean, it's the single most popular variable, there's got to be some trauma there.
The solution of x³-y!=2024 is
(x,y)=(14,6)
As check 14³=2744 and 6!=720
Неожиданная задача, но красивая!
😊😊😊👍👍👍
m=99😊
👏👏👏👏👏👏
Nice
100! Has 100 terms not 50 terms
Yes, but he grouped those 100 terms into pairs which led to 50 squared factorial terms and 50 consecutive even numbers.
This came in jee mains(or something similar book)
This problem is pretty common. I’ve seen it in more than one place
@@SyberMath well even after finishing exams these examples keep me fresh with maths