A Polynomial Equation | Problem 351

▶ Greetings, everyone! Welcome to @aplusbi 🧡🤩💗
This channel is dedicated to the fascinating realm of Complex Numbers. I trust you'll find the content I'm about to share quite enjoyable. My initial plan is to kick things off with informative lectures on Complex Numbers, followed by a diverse range of problem-solving videos.
❤️ ❤️ ❤️ My Amazon Store: www.amazon.com...
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you. ❤️ ❤️ ❤️
Recently updated to display "Books to Prepare for Math Olympiads" Check it out!!!
🤩 Playlist For Lecture videos: • Lecture Videos
🤩 Don't forget to SUBSCRIBE, hit that NOTIFICATION bell and stay tuned for upcoming videos!!!
▶ The world of Complex Numbers is truly captivating, and I hope you share the same enthusiasm! Come along with me as we embark on this exploration of Complex Numbers. Feel free to share your thoughts on the channel and the videos at any time.
▶ MY CHANNELS
Main channel: / @sybermath
Shorts channel: / @shortsofsyber
This channel: / @aplusbi
Future channels: TBD
▶ Twitter: x.com/SyberMath
▶ EQUIPMENT and SOFTWARE
Camera: none
Microphone: Blue Yeti USB Microphone
Device: iPad and apple pencil
Apps and Web Tools: Notability, Google Docs, Canva, Desmos
LINKS
en.wikipedia.o...
/ @sybermath
/ @shortsofsyber
#complexnumbers #aplusbi #jeeadvanced #jee #complexanalysis #complex #jeemains
via @UA-cam @Apple @Desmos @GoogleDocs @canva @NotabilityApp @geogebra

[@ConradoPeter-hl5ij]

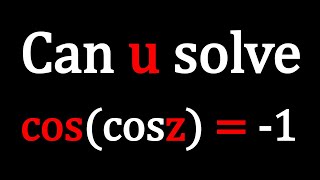
Nice video! Thanks

[@aplusbi]

Thank you too!

[@Arycke]

Nice video! Substitution is dope.
One small thing, and it is probably just a me thing, when you say "plus minus" you write minus plus. Which, for the quadratic equation, doesn't make a difference, of course.
But for angle sums, like cos, sec, (a±b) it flips to minus plus (tan and cot have them, too)
But, it was a small detail that did stand out to me.
Not wrong in this case obv, but yeah

[@aplusbi]

Good point!

[@NadiehFan]

@@aplusbi It works both ways of course. The traditional way of writing the identity for e.g. cos(α ± β) would be
cos(α ± β) = cos α·cos β ∓ sin α·sin β
the idea being that the top sign + at the left combines with the top sign − at the right and the bottom sign − at the left combines with the bottom sign + at the right. But you can equally well write
cos(α ∓ β) = cos α·cos β ± sin α·sin β
and the principle of combining signs in equal positions (top or bottom) at both sides remains valid.

[@NadiehFan]

The equation to solve is
z⁴ + z³ = z² − z − 1
This quartic equation is already in a form suitable for solving using Ferari's method: all terms of a lower than the third degree are on the right hand side and all terms of a third or fourth degree are on the left hand side.
Since z³ = 2·(z²)·(¹⁄₂z) is twice the product of z² and ¹⁄₂z we can complete the square at the left hand side by adding (¹⁄₂z)² = ¹⁄₄z² to both sides, which gives
z⁴ + z³ + ¹⁄₄z² = ⁵⁄₄z² − z − 1
or
(z² + ¹⁄₂z)² = ⁵⁄₄z² − z − 1
Next, we can take any number k and add 2k(z² + ¹⁄₂z) + k² = 2kz² + kz + k² to both sides. Since (z² + ¹⁄₂z)² + 2k(z² + ¹⁄₂z) + k² = (z² + ¹⁄₂z + k)² the left hand side will then remain a perfect square regardless of the value of k. Therefore, adding 2k(z² + ¹⁄₂z) + k² = 2kz² + kz + k² to both sides of our equation we get
(z² + ¹⁄₂z + k)² = (2k + ⁵⁄₄)z² + (k − 1)z + (k² − 1)
Since the left hand side is a perfect square regardless of the value of k, we are are now free to choose k in such a way that the quadratic in z at the right hand will also be a perfect square. It is easy to see that for k = 1 both the linear term (k − 1)z and the constant term (k² − 1) at the right hand side vanish, leaving only the quadratic term (2k + ⁵⁄₄)z² which equals ¹³⁄₄z² = (¹⁄₂√13·z)² for k = 1. So, with k = 1 our equation becomes
(z² + ¹⁄₂z + 1)² = ¹³⁄₄z²
or
(z² + ¹⁄₂z + 1)² = (¹⁄₂√13·z)²
Applying the equal squares property A² = B² ⟺ A = B ⋁ A = −B which says that the squares of two quantities are equal if and only if these quantities themselves are either equal or each others opposite this gives
z² + ¹⁄₂z + 1 = ¹⁄₂√13·z ⋁ z² + ¹⁄₂z + 1 = −¹⁄₂√13·z
and therefore
z² + ¹⁄₂(1 − √13)z + 1 = 0 ⋁ z² + ¹⁄₂(1 + √13)z + 1 = 0
Now we only need to solve these two quadratic equations using the quadratic formula to obtain all four roots of the original quartic equation.

[@scottleung9587]

I got the non-real solutions right, so I assume my real solutions are correct too.