Daping Weng, part 1, "Cluster structures for Legendrian links"

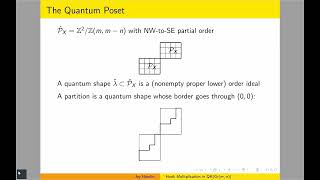
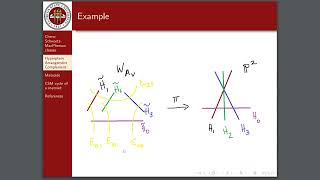
Abstract: A Legendrian link is a link in R^3 satisfying certain tangential conditions. One interesting problem to study is to distinguish different exact Lagrangian fillings in the symplectic 4-ball for the same Legendrian link. For a large family of Legendrian links that can be presented as closures of positive braids, we construct a Legendrian invariant geometric space called the flag moduli space, and show that these flag moduli spaces carry cluster structures. Moreover, we employ these cluster structures to help us distinguish exact Lagrangian fillings (which we refer to as the “filling-cluster correspondence”). This approach has led to the solution of the “infinitely-many-fillings” conjecture in 2020. In this talk, I will give some basic definitions and examples of Legendrian links and their exact Lagrangian fillings, and outline the idea on how to prove the infinitely-many-fillings conjecture using cluster structures. This talk is based on a joint work with H. Gao and L. Shen (arXiv:2008.10793) and another joint work with R. Casals (arXiv:2204.13244).