- 100
- 9 402
Schubert Seminar
Приєднався 17 жов 2021
Scott Larson, "Positivity in Weighted Flag Varieties"
Abstract: [Abe--Matsumura 2015] obtain a positivity result for a ring with basis arising from the equivariant cohomology of weighted grassmannians, but state that they do not have geometric or representation theoretic interpretations of their parameters.In joint work with William Graham, we obtain a strengthened positivity theorem for any weighted flag variety, define the basis as classes of \emph{weighted Schubert varieties}, and interpret the structure constants via \emph{weighted roots}.
In the case of weighted grassmannians, the positivity result of [AM] can be recovered from our main theorem, providing a geometric interpretation of their parameters. Along the way, we use Lie theory to generalize the definition of weighted flag varieties, prove that our main theorem also holds for equivariant Chow groups, and describe a weighted Chevalley formula.
This talk strives to illuminate the theory for the special case of weighted projective space.
In the case of weighted grassmannians, the positivity result of [AM] can be recovered from our main theorem, providing a geometric interpretation of their parameters. Along the way, we use Lie theory to generalize the definition of weighted flag varieties, prove that our main theorem also holds for equivariant Chow groups, and describe a weighted Chevalley formula.
This talk strives to illuminate the theory for the special case of weighted projective space.
Переглядів: 60
Відео
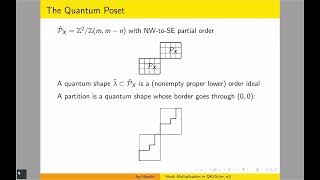
Joy Hamlin, "Hook Multiplication in the Quantum K-Theory Ring of the Grassmannian"
Переглядів 11614 днів тому
Description: Quantum K-theory is a formal deformation of K-theory that encodes Gromov-Witten invariants of the moduli space of curves meeting Schubert varieties in the Grassmannian. There are two Pieri rules, dual to each other, for multiplication in the quantum K-theory of a Grassmannian, but no positive formula for more complicated products is known. I will generalize both Pieri rules to find...
F Caraballo Alba, "The Chern-Schwartz-MacPherson cycle of a matroid"
Переглядів 3714 днів тому
Description: The Chern-Schwartz-MacPherson (CSM) class of an embeddable scheme is a generalization of the total Chern class of a proper nonsingular variety. In the case where the scheme is the complement of a hyperplane arrangement in n-dimensional projective space, this class can be computed from the matroid associated to the hyperplane arrangement. The formula for this CSM class is generalize...
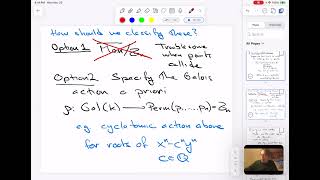
Rui Xiong, short talk, "Motivic Lefschetz Theorem for Twisted Milnor Hypersurfaces "
Переглядів 74Місяць тому
Abstract: In this talk, I will discuss the motivic decomposition of a smooth hyperplane section in twisted Milnor hypersurfaces. The key feature of our result is the appearance of a spectrum of a particular field in the decomposition. A critical ingredient is the non-triviality of the (monodromy) Galois action on the equivariant Chow group. The steps of our proof can be likened to several theor...
Kevin Summers, short talk, "A dual basis for the equivariant quantum K-theory of cominuscule spaces"
Переглядів 33Місяць тому
Abstract: The equivariant quantum $K$-theory ring of a flag variety is a Frobenius algebra equipped with a perfect pairing called the quantum $K$-metric. It is known that in the classical $K$-theory ring for a given flag variety the ideal sheaf basis is dual to the Schubert basis with regard to the sheaf Euler characteristic. We define a quantization of the ideal sheaf basis for the equivariant...
Peter Spacek, short talk, "Minuscule posets and superpotentials for cominuscule homogeneous spaces"
Переглядів 24Місяць тому
Abstract: Minuscule posets can be considered as generalizations of Young diagrams to algebraic groups of more general types. They can be represented as “skew” Young diagrams and their combinatorics is closely related to the geometry of (co)minuscule homogeneous spaces. I will illustrate how they can be used to give a type-independent statement for mirror symmetry for the (small) quantum cohomol...
Brendan Hassett, part2, `Rationality of twisted moduli'
Переглядів 22Місяць тому
Abstract: Let M_{0,n} denote the moduli space of n-pointed rational curves - configurations of n points on the line up to projectivity. This is a rational variety. Consider twists over a non-closed field, where we specify how the Galois group permutes the n points. For example, for n=2m over the reals we might have m pairs of complex conjugate points. What can we say about rationality and irrat...
Brendan Hassett, part1, `Rationality of twisted moduli'
Переглядів 25Місяць тому
Abstract: Let M_{0,n} denote the moduli space of n-pointed rational curves - configurations of n points on the line up to projectivity. This is a rational variety. Consider twists over a non-closed field, where we specify how the Galois group permutes the n points. For example, for n=2m over the reals we might have m pairs of complex conjugate points. What can we say about rationality and irrat...
Marco Castronovo, part 2, `Cluster gluings and open-string Schubert calculus'
Переглядів 28Місяць тому
Title: Cluster gluings and open-string Schubert calculus Abstract: When is a gluing of affine schemes affine? I will state a complete but conjectural answer when the pieces are tori, and the gluing maps are cluster mutations in the sense of Fomin-Zelevinsky. The combinatorics of Demazure weaves allows to prove the conjecture in interesting cases, notably those in which there are finitely many t...
Marco Castronovo, part1, `Cluster gluings and open-string Schubert calculus'
Переглядів 45Місяць тому
Title: Cluster gluings and open-string Schubert calculus Abstract: When is a gluing of affine schemes affine? I will state a complete but conjectural answer when the pieces are tori, and the gluing maps are cluster mutations in the sense of Fomin-Zelevinsky. The combinatorics of Demazure weaves allows to prove the conjecture in interesting cases, notably those in which there are finitely many t...
Brendon Rhoades, part 2 "Equivariant cohomology and orbit harmonics"
Переглядів 682 місяці тому
Abstract: The orbit harmonics deformation replaces a finite point locus $\mathcal{Z}$ in $n$-space $\mathbb{C}^n$ with a graded quotient of the polynomial ring $\mathbb{C}[x_1, ... , x_n]$. Various combinatorial varieties $X$ have cohomology rings $H^*(X)$ with Borel-style quotient presentations which may be realized using orbit harmonics. The loci $\mathcal{Z}$ involved in these constructions ...
Brendon Rhoades, part1 "Equivariant cohomology and orbit harmonics"
Переглядів 732 місяці тому
Abstract: The orbit harmonics deformation replaces a finite point locus $\mathcal{Z}$ in $n$-space $\mathbb{C}^n$ with a graded quotient of the polynomial ring $\mathbb{C}[x_1, ... , x_n]$. Various combinatorial varieties $X$ have cohomology rings $H^*(X)$ with Borel-style quotient presentations which may be realized using orbit harmonics. The loci $\mathcal{Z}$ involved in these constructions ...
Irit Huq-Kuruvilla, part2, Quantum K Rings of Partial Flags, Coulomb Branches, and the Bethe Ansatz
Переглядів 672 місяці тому
Abstract: There are two major predictions for the quantum K ring of a partial flag: One comes from quantum field theory, where the ring is the OPE ring associated to a 3D GLSM. The other comes from work identifying the quasimap version of the ring with the Bethe algebra associated to a quantum integrable system. These predictions have a mysterious set of equations in common. We give a geometric...
Irit Huq-Kuruvilla, part1, Quantum K Rings of Partial Flags, Coulomb Branches, and the Bethe Ansatz
Переглядів 712 місяці тому
Abstract: There are two major predictions for the quantum K ring of a partial flag: One comes from quantum field theory, where the ring is the OPE ring associated to a 3D GLSM. The other comes from work identifying the quasimap version of the ring with the Bethe algebra associated to a quantum integrable system. These predictions have a mysterious set of equations in common. We give a geometric...
Sara Billey, part 2: `A Journey from Schubert Style Rank Functions via ASM's to Quilts on Posets'
Переглядів 483 місяці тому
We present new objects called quilts of alternating sign matrices with respect to two given posets. Quilts generalize several commonly used concepts in mathematics. For example, the rank function on submatrices of a matrix gives rise to a quilt with respect to two Boolean lattices. When the two posets are chains, a quilt is equivalent to an alternating sign matrix and its corresponding corner s...
Sara Billey, part 1: `A Journey from Schubert Style Rank Functions via ASM's to Quilts on Posets'
Переглядів 493 місяці тому
Sara Billey, part 1: `A Journey from Schubert Style Rank Functions via ASM's to Quilts on Posets'
Cristian Lenart, part 2, `A Chevalley formula for the K-theory of semiinfinite flag manifolds'
Переглядів 508 місяців тому
Cristian Lenart, part 2, `A Chevalley formula for the K-theory of semiinfinite flag manifolds'
Cristian Lenart, part 1, `A Chevalley formula for the K-theory of semiinfinite flag manifolds'
Переглядів 888 місяців тому
Cristian Lenart, part 1, `A Chevalley formula for the K-theory of semiinfinite flag manifolds'
Elie Casbi, p. 2, Representations of affine quantum groups and the homology of affine Grassmannians
Переглядів 428 місяців тому
Elie Casbi, p. 2, Representations of affine quantum groups and the homology of affine Grassmannians
Elie Casbi, p 1, Representations of affine quantum groups and the homology of affine Grassmannians
Переглядів 1128 місяців тому
Elie Casbi, p 1, Representations of affine quantum groups and the homology of affine Grassmannians
Daping Weng, part 2, "Cluster structures for Legendrian links"
Переглядів 609 місяців тому
Daping Weng, part 2, "Cluster structures for Legendrian links"
Daping Weng, part 1, "Cluster structures for Legendrian links"
Переглядів 1019 місяців тому
Daping Weng, part 1, "Cluster structures for Legendrian links"
Nicolas Perrin (part 1) `Positivity of Grassmannian quantum K-theory'
Переглядів 1009 місяців тому
Nicolas Perrin (part 1) `Positivity of Grassmannian quantum K-theory'
Nicolas Perrin (part 2) `Positivity of Grassmannian quantum K-theory'
Переглядів 1079 місяців тому
Nicolas Perrin (part 2) `Positivity of Grassmannian quantum K-theory'
Changzheng Li, (part 2) "A Plucker mirror for partial flag varieties and quantum Schubert calculus"
Переглядів 3510 місяців тому
Changzheng Li, (part 2) "A Plucker mirror for partial flag varieties and quantum Schubert calculus"
Changzheng Li, (part 1) "A Plucker mirror for partial flag varieties and quantum Schubert calculus"
Переглядів 3510 місяців тому
Changzheng Li, (part 1) "A Plucker mirror for partial flag varieties and quantum Schubert calculus"
Arun Ram, part1 "Generalised divided differences and Monk rules"
Переглядів 6910 місяців тому
Arun Ram, part1 "Generalised divided differences and Monk rules"
Arun Ram, part2 "Generalised divided differences and Monk rules"
Переглядів 2010 місяців тому
Arun Ram, part2 "Generalised divided differences and Monk rules"
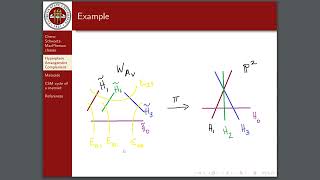
Chi Hong Chow, part 2, Flag varieties and mirror symmetry
Переглядів 7411 місяців тому
Chi Hong Chow, part 2, Flag varieties and mirror symmetry
Chi Hong Chow, part 1, Flag varieties and mirror symmetry
Переглядів 12311 місяців тому
Chi Hong Chow, part 1, Flag varieties and mirror symmetry