
- 20
- 2 220
Samuel Tréton
Приєднався 8 чер 2021
Stability of the trivial equilibrium in degenerate monostable reaction-diffusion equations
This talk adresses the long-term behavior of reaction-diffusion equations $\partial_{t} u = \Delta u + f(u)$ in $\mathbb{R}^{N}$, where the growth function $f$ behaves as $u^{1+p}$ when $u$ is near the origin.
Specifically, we are interested in the persistance \textit{versus}~extinction phenomena in a population dynamics context, where the function $u$ represents a density of individuals distributed in space.
The degenerated behavior $f(u)\sim u^{1+p}$ near the null equilibrium models the so-called Allee effect, which penalizes the growth of the population when the density is low. This effect simulates factors such as inbreeding, mating difficulties, or reduced resistance to extreme climatic events.
We will begin the presentation by discussing a result linking the questions of persistence and extinction with the dimension $N$ and the intensity of the Allee effect $p$, as established in the classical paper by Aronson and Weinberger (1978).
This result is closely related to the seminal work of Fujita (1966) on blow-up \textit{versus} global existence of solutions to the superlinear equation $\partial_{t}u = \Delta u + u^{1+p}$.
Following these preliminary results, we will focus on a reaction-diffusion system involving a \glmt{heat exchanger}, where the unknowns are coupled through the diffusion process, integrating super-linear and non-coupling reactions.
An analysis of the solution frequencies for the purely diffusive heat exchanger will allow us to estimate its \glmt{dispersal intensity}, which is a key information for addressing blow-up \textit{versus} global existence in such semi-linear problems.
This work represents a first step toward Fujita-type results for systems coupled by diffusion and raises several open questions, particularly regarding the exploration of more intricate diffusion mechanisms.
Specifically, we are interested in the persistance \textit{versus}~extinction phenomena in a population dynamics context, where the function $u$ represents a density of individuals distributed in space.
The degenerated behavior $f(u)\sim u^{1+p}$ near the null equilibrium models the so-called Allee effect, which penalizes the growth of the population when the density is low. This effect simulates factors such as inbreeding, mating difficulties, or reduced resistance to extreme climatic events.
We will begin the presentation by discussing a result linking the questions of persistence and extinction with the dimension $N$ and the intensity of the Allee effect $p$, as established in the classical paper by Aronson and Weinberger (1978).
This result is closely related to the seminal work of Fujita (1966) on blow-up \textit{versus} global existence of solutions to the superlinear equation $\partial_{t}u = \Delta u + u^{1+p}$.
Following these preliminary results, we will focus on a reaction-diffusion system involving a \glmt{heat exchanger}, where the unknowns are coupled through the diffusion process, integrating super-linear and non-coupling reactions.
An analysis of the solution frequencies for the purely diffusive heat exchanger will allow us to estimate its \glmt{dispersal intensity}, which is a key information for addressing blow-up \textit{versus} global existence in such semi-linear problems.
This work represents a first step toward Fujita-type results for systems coupled by diffusion and raises several open questions, particularly regarding the exploration of more intricate diffusion mechanisms.
Переглядів: 31
Відео
Soutenance de thèse - Samuel Tréton
Переглядів 20Місяць тому
Lien vers le manuscrit : samueltreton.fr/shares/PhD_manuscript_TRETON_SAMUEL.php Lien vers mes thématiques de recherche : samueltreton.fr/recherche/ TITRE : Analyse de Dynamiques d’Échanges Microscopiques et Macroscopiques pour l’Écologie et l’Épidémiologie RÉSUMÉ : Cette thèse porte sur la dérivation et l’analyse de modèles de populations structurées en espace, de nature stochastique et déterm...
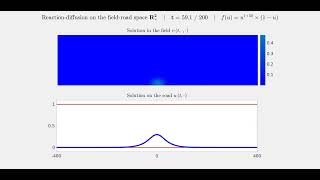
An Interacting Particle System Journey towards the Field-Road Diffusion Model
Переглядів 409 місяців тому
This presentation explores the field-road diffusion model developed in 2012 by Berestycki, Roquejoffre, and Rossi. This parabolic system aims to capture the significant dispersal effects induced by lines of fast diffusion, with wide-ranging applications in population dynamics, ecology, and epidemiology. Initially, we will introduce the model, emphasizing its ability to simulate accelerated spre...
Blow-up vs. global existence for a Fujita type Heat echanger system
Переглядів 61Рік тому
Dans cette présentation, nous parlerons de phénomènes d'explosion en temps fini survenant pour certains problèmes de réaction-diffusion sur-linéaires. Nous commencerons par une introduction aux résultats fondateurs du mathématicien japonais H.Fujita concernant l'équation de la Chaleur altérée par l'ajout de l'inconnue élevée à la puissance 1 p dans le second membre. Dans son travail de 1966, Fu...
Diffusive Dialogues: Mathematical Models of Individual Exchanging Across Spatial Domains
Переглядів 27Рік тому
In this talk, we examine mathematical models that describe the diffusion and exchange of individuals across spatial domains. We begin with the field-road model, emphasizing its biological foundations and its importance in understanding fast diffusion channels in population dynamics and ecology. Following this, we explain how to derive the explicit solutions for the field-road model and provide ...
Field-road RD-system: extinction with a reaction with Allee effect in the field
Переглядів 212 роки тому
Further explanations here: www.samueltreton.fr/reation_diffusion_champ_routeEN.html and here: www.samueltreton.fr/rechercheEN.php
Field-road RD-system: invasion with a KPP-reaction in the field
Переглядів 242 роки тому
Further explanations here: www.samueltreton.fr/reation_diffusion_champ_routeEN.html and here: www.samueltreton.fr/rechercheEN.php
Brownian motion of particules on a Field Road space: the effect of the Road
Переглядів 783 роки тому
Brownian motion of particules on a Field Road space: the effect of the Road
Brownian motion of 1000 particules on a Field Road space
Переглядів 483 роки тому
Brownian motion of 1000 particules on a Field Road space
Brownian motion of 500 particules on a Field Road space
Переглядів 643 роки тому
Brownian motion of 500 particules on a Field Road space
Brownian motion of 4 particules on a Field Road space
Переглядів 603 роки тому
Brownian motion of 4 particules on a Field Road space
Numerical simultation of the Heat equation on the Field-Road space \\R^2_+
Переглядів 613 роки тому
Numerical simultation of the Heat equation on the Field-Road space \\R^2_
Hair Trigger Effect for a KPP R-D equation on a Field Road model
Переглядів 583 роки тому
Hair Trigger Effect for a KPP R-D equation on a Field Road model
Heat equation on a half-line with Robin boundary conditions (comparison of 6 cases)
Переглядів 4613 роки тому
Heat equation on a half-line with Robin boundary conditions (comparison of 6 cases)
Heat equation on a half-line with Robin boundary conditions
Переглядів 1923 роки тому
Heat equation on a half-line with Robin boundary conditions
HTE vs extinction for a R-D equation with a weak Allee effect in \\R^N
Переглядів 533 роки тому
HTE vs extinction for a R-D equation with a weak Allee effect in \\R^N
Hair Trigger Effect for a KPP R-D equation in \\R^N
Переглядів 773 роки тому
Hair Trigger Effect for a KPP R-D equation in \\R^N







Merci beaucoup Monsieur Trevor !