Відео

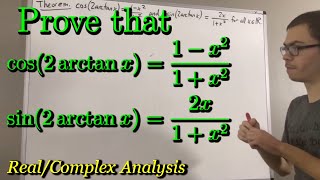
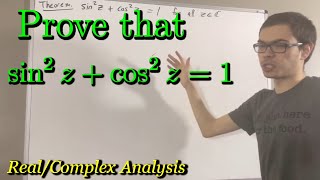
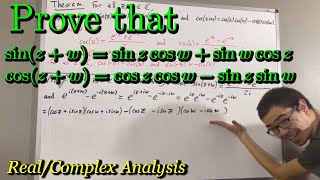
nice proof, but why make it so overly complicated? just define f(x)=|x|-|sin(x)| and analyse that function... if |x|>=1, it's clear that f(x)>=0, so we'll restrict the analysis for |x|<1 (actually it's not strictly necessary, as we can easily show that f is increasing on R+, but for simplicity's sake i'll just write it like this). f is even (so you only need to check f(x)>=0 for x>=0), and for 0<=x<=1, f is differentiable and f'(x)=1-cos(x)>=0, so f is increasing on [0,1], and since f(0)=0, f(x)>=0 for x in [0,1] (and thus for all x in [-1,1] since f is even, and then on R since f(x)>=0 in R\(-1,1)).

weird background noise.

easier proof:both abs(sinx) and abs(x) are symmetric about the y axis, so we only have to look at x>=0. The derivative of sinx is cosx, and the derivative of x is just 1, and since cosx has a maximum value of 1 when x=2npi, and abs(sin0)=0, we can say that abs(sinx) won't exceed abs(x).

I'm still looking forward to the derivation of arctan :) Thank you.

Since the function is mirrored, we can just prove it for 0 < x < pi/2. Then we can probably use the taylor expansion to show that sin(x) is always less or equal to x on that interval. (fundamental theorem of engineering works too)

Bro just draw out a triangle and it pops right out

It's a great video, I don't have the basics to fully understand the video yet. But, I really liked how you proved it using the definitions.

Why can’t you just use the unit circle and why is there an absolute value. I feel like I am misreading the question or something

Why not just use calculus? It would be much easier

I think someone can learn a lot from these proofs, but when it comes to memorizing proofs for various sentences and then reconstructing them from memory, “shorter” proofs that don't go into so much detail would be easier. Perhaps something along these lines could be introduced in the future, that would be great :)

Why is arctan involved at all ? Why not just use eulers identity e^ix and be done? Thanks for sharing

I am a first year so this may be an elementary question. Is this actually the most fundamental way to prove this result?

Wow. Bro really is speed running analysis.

Great

Great video! Keep up the good work

I'm still waiting to see how you tie this to triangles :)

If you only need proof for the case z and w are real, then writing e^(i(z+w)) = (e^(iz) e^(iw)) and collecting like terms proves both formulas all-in-one. I'm not sure if there's a way to formalize "collect like terms" so that the shortcut still functions a rigorous proof. In any case, if one takes for granted that the identities exist but forgets what they are, the two-for-one will spit out the correct answers by simple follow-your-nose computation.

You good dawg!

Amazing explanation ! Thank you so much

I like it! Unexpected

I feel like the property at 2:42 is derived from this exact equality, so doesn't that mean its proving itself, and hence not really a proof? I can solve x^2 = 25 by "recalling" 25 is the square of 5, that doesn't make that a proof does it? A beautiful proof if this exact problem is using the taylor expansion of e^x, and substituting (ix) for x, and seeing that the real part is equal to the taylor series for cos(x) and the imaginary part the taylor series of sin(x).

uuuuuuuuum actually the first thing you wrote in red is false, the first thing is a number while the secon is a function

Who let this third grader on UA-cam and make math videos? Bro this is a circular argument....

I knew you were gonna make a video about this property ! 😂

I'm interested to see a proof or derivation for the limit definition of arctan(x) using that sequence you noted. Do you have any reference to share by chance? Thank you. P.S. I could never imagine it would take 16 minutes to peove that tan of 45 deg is 1 lol.

Nice and quick one

can you prove sin(x) = x and cos(x) = 1 for small x

I'm pretty sure the definitions of cos z and sin z are based on the identity and this is just circular reasoning hence not being a valid proof. A taylor series proof is a much better way to prove this.

Great

Bro proved nothing 😭

Are there any non-over-the-top cases where we can show there exists a bijection between two sets but can't construct it?

I'm curious to see if we will get to prove that cos and sin are related to pi (the one defined from circles and not the one defined in the previous videos, even if of course they are the same) !

First

What is the process by which delta is suddenly set to be x^2+1/ xo-x??

or you ask yourself the question: For which x is tan(x) = 1 and if you are a little familiar with trigonometry, you know that tan(Pi/4) = 1 and you are done in a few seconds ;-)

These proofs always do my head in. I was thinking what is it in this proof that means you can't apply the same logic to sin(x) limit doesn't exist by saying epsilon = 2 and setting x = k.pi or even setting epsilon = 1? By eliminating the "one over" everywhere gets the same....or is it the archimedian step that is actually key. Sometimes these videos need (possibly) stupid examples to show the value of these proofs.

I could have saved you a lot of time by simply showing that the sequence 8,9,10 is a consecutive sequence of positive integers that are not prime numbers.

I look forward to these videos every day

My immediate instinct was to integrate the derivatives and immediately prove it. If t > 0, 1/(1+t^2)^(3/2) < 1/(1+t^2) < 1 and integrate from 0 to x.

You shouldn't speed up parts of your videos. People need time to think, while they are watching. Otherwise great stuff you are producing!

make a vid on why that sequence converges to arctan 😂 i love these vids btw!!

Such a nice proof!

I'm hooked to this series. Thank you for the effort of putting together these videos!

I appreciate this series of real analysis and your channel overall because it gives me another perspective in math. Did u learn this things in college or u read about them for yourself? I am curious because i didnt saw arctan as a limi before.

great video. i just finished a calc class with infinite series (not sure if commonly referred to as calc 2 or 3) and was super grateful for the development of the ratio test thanks for taking your time to go back and explain what’s going on! it’s super helpful looking forward to seeing more vids!

Keep up the great work

THIS VID REALLY HELPED TY!!

For 2 seconds I thought you would forget the second therefore conclusion hehe! Great video, thanks!

The yt algorithm hid this from me bc i used x and y in the search prompt. Just pieced it together from your earlier proofs before finding this, but I'm glad I had to do it since this channel is exactly how I need it explained. Not too long, but with all necessary info for formal proofs

Really helps catching up on early uni math, thx :)