Відео

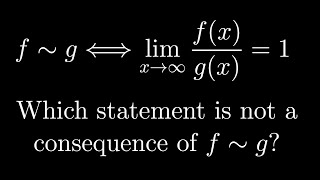
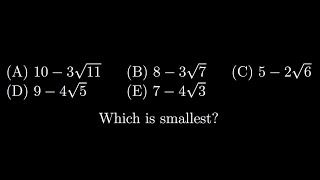
Ha ha! The title board problem was substantially more complex (and fun) than what this turned out to be. I got 355 / 3^11 for the case that every vector in { (1,1), (1,2), (2,1), (2,2), (3,1), (3,2) } is equally likely.

This seems harder than it is. The difference of coordinates for (1,1)=0 for (3,2)=1 Ans for result (10,8)=2 so if there is a way the vectors need to be 4x (1,1) and 2x (3,2) they indeed add to (10,8) so solutions exist. Number of solutions is the number of choosing the positions of the big vectors in a list from 1 to 6 =6*5/(1*2)=15 cases Total possible vectors to generate =2^6=64 P=15/64 (desirable/total cases)

Interestingly, also option C) is a valid consequence, if one has the additional assumption that g has a finite limit, ie. lim g(x) = C, since then lim exp(f(x) - g(x)) = lim exp(g(x) * (f(x)/g(x) - 1)) = exp(lim g(x) * lim (f(x)/g(x) - 1)) = exp(C * 0) = 1.

For e I think the Taylor expression would show that the limit is 1+f(X)+f^2(X)/2!+...

Spot on, I had just never heard that word, which always throws you a bit, but OK after you just get it clear in your head what they are asking for

I noted that in each answer we have a form (a - b) = (a² - b²) / (a + b) = 1 / (a + b). But the values of (a+b) are easily seen to be largest for (A), as the individual values of both a and b are largest for (A); so the value of (a - b) is smallest for (A). Hence answer (A).

By reading the solutions I saw the line is given as Point+Vector*parameter so I might be lazy and check if the point is on both planes. I can notice the planes are not parallel as coefficients of X,y,z are not proportional with constants giving null solutions. A excluded B excluded as planes do not intersect in a point C P(0,0,7) does not verify second plane equation as -21|=0 D P(0,3,1) 0+3*3-2*1=7 verified 2*0+3-3*1=0 verified

I followed the same logic until a^3-3a^2+3=0 Let g(a)=a^3-3a^2+3 then g'(a)=3a^2-6a=0 a=0 or a=2 are points of extrema because the quadratic g'(a) changes sign in those points g(0)=3 g(2)=-1 So g(a) has 3 roots as it grows from -inf to 3 then decreases to -1 and goes up to +inf

I did it the same way as you, but as soon as you had the cubic in a, I differentiated again to find coordinates of the turning points to sketch the curve

I evaluated, from the plane normals as given above in standard form, | i j k | det ( | 2 1 -3 | ) = 7 i + j + 5k = (7, 1, 5) as the direction vector for the intersection line. | 1 3 -2 | Thus answer (D).

I got the right answer, but it took me a while to remember how to do parameterization. Fun problem!

I looked up some random textbook on internet for multivariable functions. A=d2f/(dx)^2=2 B=d2f/(dxdy)=-2 C=d2f/(dy)^2=6y We need to calculate the discriminant B^2-AC I) x=y=0 then B°2-AC=4>0 not a point of extrema II) x=y=2/3 B^2-AC=4-(2)(6*2/3)=-4 If A<0 then it is maximum but in our case A>0 sonwe got our local minimum point. Because there exists y such that f(2/3,y)<f(2/3,2/3)

I found some books about multivariable surface calculus but my memory of doing the subject is not great I know you usually want df/dx=0 and df/dy=0 plus some additional conditions to know if it is Mon/max or saddle point In this case df/dx=0 2x-2y=0 so X=y And df/Dy=0 -2x+3y^2=0 So A is true in a sense it is necessary but not sufficient condition B is false C not sure as (df/dx^2)^2=2 and (df/dy^2)^2=3y =0 at (0,0) D obviously false E f(X,y)=(x-y)^2-y^2+y^3=(x-y)^2+y^2(y-1) (x-y)^2 has a valley at X=y and y^2(y-1) is negative when y<1 and positive otherwise so it is only increasing as y grows so this should be false

I started by trying to square stuff, too, but gave it up on that right away. After a couple minutes staring, I realized it was all of the form sqrt(x) - sqrt(x - 1), which quickly presented the correct solution.

The way I see it we are comparing 2 radicals For A √100-√99 B √64-√63 C √25-√24 D √81-√80 E √49-√48 Obviously A is smallest difference from an inequality. Using calculus 1/(2√(n+1)<√(n+1)-√n<1/(2√n) from T Laplace applied on f(x)=√x on interval [n,n+1]

Well done, nice solution. Thought it was a lovely question, I could not do it. Solution was to note for instance 10 - 3√11 = √100 - √99, 8 - 3√7=√64 - √63. Each other option follows the same pattern, all are the difference of square roots which are one apart. Could write each as √x -√x-1.The bigger the numbers get, the smaller will be the difference. You could rationalize which leads to 1/ √x + √x-1, to convince yourself this is correct. Or graph it. Hence the answer is A.

I did it without (much) calculation. If a line has slope e^p, how long does it take that line to rise from 0 to e^p?

I didn't bother to solve it I was just looking at the variants and I think all of them involving p-a or p+a are situationally false so I would g o with A. Line equation is obviously y-e^t=e^t(x-t) when t is the point of tangency finding a: y=0 t=p -e^p=e^p(a-p) a-p=-1 and for b and Q it would result b-q=-1 Intuition too stronk :)

Did it virtually the same. Found equation of tangents at both points. Worked out where both crossed the x-axis. Lead to a+1-p=0 and b+1-q=0, set them equal gives answer C.

Nice. I worked just from the title board, and spotted that a1 = 1 a2 = 3 a3 = 6 a4 = 10 and then verified the induction that a_n = n (n+1) / 2. Took about the same time as your method, so no particular advantage to either.

I considered a_n as a product of all past terms then used telescoping to say a_(n+1)=(n+2)(n+1)/2 Same method just a different starting point

My idea to solve is that the point lies on the segment uniting the circle's centres. Diff(y)=4-1=3 Diff(x)=5-1=4 Distance=√(3^2+4^2)=5 Sum of radiuses=2+1=3 so indeed circles do not intersect So the closest point to second circle is if we scale the vector from centre to centre down from 5 units to 5-2(radius of distant circle)=3 units P(x,y)=(1,1)+3/5*(4,3)=(3.4,2.8)

You can always compute trig ratios of pi/3 and pi/6, with no memorisation, simply by bisecting an equilateral triangle.

I have no idea what sin(π/6) is. However, sin(30°) is obviously 1/2.

Numerator = 6^(r+s)*12^(r-s)=2^(r+s)*3^(r+s)*2^(2r-2s)*3^(r-s)=2^(3r-s)*3^(2r) Denominator= 8^r*9^(r+2s)=2^(3r)*3^(2r+4s) this is an integer if and only if the exponents of the numerator >= those of denominator 3r-s>=3r => s<=0 2r>=2r+4s s<=0 again

You got the answer by 1.32. 12 triangles, each triangle area can be found using ½ a.b. sinΘ. Hence 12(½. 1.1.sin30). Sin30 =½, hence answer is 3.

As other commenters have rightly said, the standard approach for proving divisibility results of this kind (where the expressions involve exponential functions) is induction.

Induction definitely way to go. If 5^(2n+1) + 2^(2n+3)*3^n = 13*k(n), then the next term 5^(2n+3) + 2^(2n+5)*3^(n+1) = 25*5^(2n+1) + 12*2^(n+1)*3^n = 13 * 5^(2n+1) + 12*(5^(2n+1) + 2^(n+1)*3^n) = 13 * 5^(2n+1) + 12*13*k(n) = 13*(5^(2n+1) + 12*k(n)). Similarly, if 2^(n+2) + 3^(n+2)*5^n = 13*k(n), then the next term 2^(n+3) + 3^(n+3)*5^(n+1) = 2*2^(n+2) + 15*3^(n+2)*5^n = 2*2^(n+2) + 13*3^(n+2)*5^n + 2*3^(n+2)*5^n = 2*(2^(n+2) + 3^(n+2)5^n) + 13*3^(n+2)*5^n = 2*13*k(n) + 13*3^(n+2)*5^n = 13*(2*k(n) + 3^(n+2)*5^n).

I think h(x) is quite easy to determine as e^x is a constant with regards to t so h(x)=e^x(e^(x^2)-1) h'(x)=e^x(e^(x^2)-1+2xe^(x^2)) plug in 1 and get h'(1)=e(e-1+2e)=3e^2-e

I haven't tried, but I would recommend trying proof by induction (numerator and denumerator separately, i.e. that both are divisible by 13)

I beat my head against this one with no luck.

Got nowhere with this. Tried to factorise numerator and denominator, and use fact 13 is prime, or hoped for some cancellations. Maybe show each indivual term is =0 (mod13)??? Interested to know which book this came from.

Thanks for picking this up. I am curious about your method My approach (and the one on the book) is usually getting everything to the same power for the numerator we get: 5*25^n+8*4^n*3^n=5*(26-1)^n+8*(13-1)^n by expanding the binomial expressions you get a lot of factors containing 2*13 or13 to various powers and a last term equal to (-1)^n*5+(-1)^n*8 which also adds to a multiple of 13 Denomiantor: 4*2^n+9*(3*5)^n=4*2^n+9*(13+2)^n= Multiples of 13+ 4*2^n+9*2^n Edit: as I have seen in some of your videos I was expecting to see mathematical induction from you

Viewer submissions are always the hidden gems of math videos! This one really had me scratching my head in the best way. It’s fascinating how a simple radical can lead to such elegant patterns. Reminds me of the time I stumbled across a similar problem on SolutionInn while prepping for exams, it’s amazing how breaking things down step-by-step makes even the wildest problems approachable. Great work putting this together!

It is fairly easy to eliminate the answers A, B, C and E with some basic inequalities: From 44^2=1936 < 2016 < 45^2 = 2025 and 7^2=49 < 56 < 8^2 = 64, we get 51 < √2016 < 53 (*). If k <= 5/4, then 14^k <= 16^(5/4)=32. So, from (*) we get k > 5/4. And, if k >= 5/2, then 14^k >= 9^(5/2) = 243. So, from (*), we get k < 5/2. So, 5/4 < k < 5/2.

2:10 The divisibility rules from primary school can still be useful sometimes: 504 is divisible by 4 because 04 is!

If we do a variable change y^2=x then 2ydy=dx and integral becomes Integral (0->sqrt(a)) of 2y(y+y^4)dy= 2/3 a^(3/2)+1/3 a^(6/2)=1/3(2a*sqrt(a)+a^3)=5 (looks like my substitution was useless and I didn't get anything simpler than doing it directly with square root being power 1/2) if a=b^2 then 2b^3+b^6=15 b^6+2b^3-15=0 -> (b^3+7)(b^3-5)=0 so b^3=5 or -7 and then a is 5^(2/3) or 7^(2/3) I wonder where did the extraneous root came from maybe if i just work with a 2a*sqrt(a)=15-a^3 squaring 4a^3=(15-a^3)^2 4a^3=225-30a^3+a^6 so a^6-34a^3+225=0 25+9=34 so (a^3-25)(a^3-9)=0 so we also get 5^(2/3) and 3^(2/3) solutions I will check video cause I find it hard to verify which solution is correct easily 1/3( 2*3^2/3*3^1/3+3^2)=1/3*(15)=5 i guess it's not that hard just me being lazy if iw as doing question I would not even bother verifying for extraneous roots with multiple choices as I would have picked 5^(2/3) Edit: Do not mind my algebra at first tryout . You saw nothing

Isn't the first function a de with y''-2y'+3y=0 which has the associated equation r^2-2r+3=0 R1,2=(2+-√4-12)/2=1+-√2i the solutions for the d.e are y=C1*e^(x*r1)+C2e^(x*r2) Obviously if C1|=C2 then we get a function over R with values in C Second equation has solution g(X)=C1*e^(0x)+c2*e^(3x) General solution but only g(x)=C*e^(3x) will work And is a continuous function Last one looks hard to figure out but we already have a valid solution to question:) as D) Edit: Now of further thinking h0(X)=C1e^(-x)+C2*e^(X) Will satisfy h''=h but if we have h(X)=h0(X)-1 it will satisfy original eq

I love these videos, thank you very much

3/2

Picture shows x*e^b but video shows e^bx

It gets a bit easier if you keep working with prime factors as much as possible after (correctly!) calculating them. That saves a lot of large multiplications. √(2⁵·3²·7) + √(2³·7) = 14^k Square both sides 2⁵·3²·7 + 2³·7 + 2·2⁴·3·7 = 14^2k 2³·7·(2²·3² + 1 + 2²·3) = 2³·7·49 = 2³·7³ = 14^2k 2k = 3 k = ³⁄₂

Alternatively; 1+2x+3x^2+4x^3+... can be rewriten as 1+x+x^2+x^3+... x+x^2+x^3+... x^2+x^3+... x^3+... taking the sums of each line for |x|<1 gives while factoring out x^n to get geometric series gives 1/(1-x) x/(1-x) x^2/(1-x) . . . factoring out [1/(1-x)] gives yet another geometric series [1/(1-x)]*[1/(1-x)]=1/(1-x)^2

Another video where I'm screaming at the computer as you make an arithmetic mistake! My approach was to factor the numbers, and I quickly realized it was 12 sqrt(14) + 2 sqrt(14), which is 14 sqrt(14), which is 14^(3/2).

Thanks for doing question, I did not get the answer. Felt for you with error whilst doing prime factors of 2016. The solution took prime factors of both numbers 2016= 2^5 x 3^2 x 7, write as 2^4 x 3^2 x 14. 56= 2^3 x 7, write as 2^2 x 14. Take out even terms from under radical, leads to 14√14. Hence answer 3/2. NIce question even thou I could not do it.

Thank you for your video. I suggest expressing the 3 solutions as a-r, a and a+r, which saves a significant amount of calculation time.

This is pretty easy problem just let f(x)=e^(bx) and g(x)=10x Iy is obvious b>0 otherwise we get an intersection. We are looking for a point c for which f(c)=g(c) and f'(c)=g'(c) I was wondering if there was a way to use T Fermat for a function h=f-g but if we do not know the minimum it doesn't seem likely to work. So with the standard workout we go 10c=e^(bc) 10=b*e^(bc) => e^(bc)=10/b => 10c=10/b so c=1/b 10c=e^1 c=e/10 so b=10/e This is strange. I make a substitution error and got b=ln10 which seems like it will work as 10x is tangent to 10^x at x=1

Hi, thanks for doing the question. Sorry wording caused you some confusion, I copied it verbatim from the textbook it was in. The suggested solution was using a similar technique for finding the sum to n terms of a GP. Multiply through by x, subtract the two equation leading to the sum to n terms you got. And obviously as n → infinity leads to the answer required. So did not use calculus as you did, nice to see another method.

The way I thought of it: Every number in P(n) has a unique prime factorization: p × (prime factorization of n). So P(n) ∩ P(m) is empty, unless the prime factorization of n and m differ by exactly one prime each. 12 = 2×2×3 and 20 = 2×2×5 is the only one of the answers that work.

I see this as stating that Pn is formed of all numbers of the form n*p where p is a prime. From this observation intersection of Pn and Pm is the set of given by existing primes p,q such that p*n=q*m which means that either p/q=m/n. If p and q are to be primes it follows that m/n=1 and p=q or that m and n are prime themselves or have a gcd that will reduce them to primes So solution will be 1/23 not good. 7/21=1/3 not good 12/20=3/5 will work. 20/24=5/6 not good 5/25=1/5 not good because 1 and 6 are not primes