How to Learn Probability Distributions
Вставка
- Опубліковано 3 січ 2025
- The machine learning consultancy: truetheta.io
Join my email list to get educational and useful articles (and nothing else!): mailchi.mp/tru...
Want to work together? See here: truetheta.io/a...
In this video, I share a perspective on probability distributions that makes understanding and retaining them easier.
SOCIAL MEDIA
LinkedIn : / dj-rich-90b91753
Twitter : / duanejrich
Enjoy learning this way? Want me to make more videos? Consider supporting me on Patreon: / mutualinformation
Sources and Learning More
The incredible chart mapping out the relationships among probability distributions comes from Larry Leemis and Jacquelyn McQueston[1]. They and many other contributors put together a website providing all the details on that chart : www.math.wm.edu...
Wikipedia has two [2][3] articles that provided a lot of interesting relationships. Also, John D. Cook proves that the student-T is a mixture of normals in [4].
[1] Leemis, L. & McQueston, J.T. (2008), Univariate Distribution Relationships, The American Statistician, Vol. 62, No. 1
[2] Relationships among probability Distribution, Wikipedia, en.wikipedia.o...
[3] Compound Probability Distribution, Wikipedia, en.wikipedia.o...
[4] Cook, J.D. (2008), Student-T as a Mixture of Normals, www.johndcook....
Extra Notes
In this video, I label the Poisson a "continuous" distribution, which is certainly not true in the general context - it is as discrete as they come. A better label than "continuous" would directly reference the specific limit that is taking place. Also, such a label would separate them from the other continuous distributions that can be reached with different limits. Thank you mCoding for pointing this out.







It's so great. You're filling the probabilistic/statistical gap that 3B1B leaves. I am so glad to have found you
Super happy to hear that! I’ll keep it coming. Thank you!
Thats a great way to put it. Spot on!
Exactly. That's what i always felt!! Really great content for all those inclined to Statistics more than Maths!
Grant said he's likely to make a series on statistics next year. Thanks to this channel, the bar is set pretty high! :)
Super cool. @10:25 - as a direct contributor to this project almost 10 years ago with Dr. Leemis, this is an absolute HONOR!!!
I was hoping to get a comment from one of you! Yea that thing is a beast! There were so many connections in there that I hadn't heard of. Really awesome stuff!
Another great explanation, thanks for linking the chart too! My only qualm with this one is that I would not put Poisson on the continuous side of things. I know that Binomial(n,p) converges to Poisson(lambda) when n/p converges to lambda and n to infinity, so it is a limit of discrete distributions. But the Poisson distribution is the keystone of discrete probability theory, and it is of course not a continuous distribution as you mentioned. It can be used to count continuous things, as in using a Poisson point process which can live in a continuous-time world, but just a single Poisson distribution does not share this continuous characteristic. The continuous analog of the Poisson point process is of course the Brownian motion.
2 mCoding comments in a day? It’s a good day!
Regarding your qualm, this was exactly the piece I was a bit uncomfortable with too (hence the note). In the general context, it’s clear the Poisson distribution is certainly NOT a continuous distribution. But to complete the story, I felt it was ok to slide by. A better solution might be to not use the title “continuous”, but rather something that mentions its specific limit.
It’s a good point. So I’ve included a clarification in the description on this point. Thank you for it!
In my field (simulation modeling), the most important thing to realize (which the stories do say, though not as clear as I would like) is that the Poisson distribution and the Exponential Distribution are inverses of each other. (That and the Exponential's Markovian properties, but that's a bit more advanced.)
I had given up on understanding probability distribution, thinking that I am the dumbest guy in the world, then I found your video, making the concept crystal clear. Wishing the stats books were as good in explanation.
This is so great man. I have one year left of my Stats degree and I've been slowly teaching myself how to make videos using Manim. These videos are the closest thing I've seen to my vision of a Stats UA-cam channel that fills the void currently on UA-cam. If you need video ideas, I think a whole series on how the different distributions relate, and thinking about them intuitively would be very valuable for people trying to learn this stuff (myself included).
Very cool! I had a feeling others would appreciate the pull-no-punches technical stuff. I'd be very interested to see what you put together on UA-cam. Manim opens up a beautiful world.
Regarding that idea, it's quite interesting. I may get to something like that down the line, by right now, there are quite a few things in queue.
Thanks!
Literally first donation ever! Thank you very much!
Dedicating my first comment ever to saying these videos are amazing, keep doing what you’re doing. Would love to see more probability and stats videos
That means a lot to me! Thank you very much. And yes, will do. There’s more coming!
I just came from your Quora post about your dream about dreaming about trying to find the volume of a 4D sphere.
I subscribed already. These videos are amazing and I feel like they will come in handy when I take ML classes later on in my degree. Keep it up!!
Oh yea! Totally forgot about that post - the Quora days were fun
I hope this channel gets the attention it deserves soon
Thank you! I’ll keep trucking away so I think it will. Appreciate the support
Every single video on this channel is priceless.
I am just fascinated by your videos.
I have never written youtube comments before, this is my first youtube comment in my entire life.
I would prefer to keep watching your videos rather than playing video games. Addictive!
Wow dude this is one of the nicest comments I've gotten. Thank you brother it means a lot! I haven't posted in awhile only b/c I'm working on a big series, but I'm shooting it this weekend so it should be there soon. Super pumped you're enjoying it!
@@Mutual_Information I appreciate all your work! I can't wait to watch your next enlightening videos!
Awesome video again! How could i live my live up until now without this perspective on these probability distributions... you shattered my world!
Haha that’s is some flattery! I’ll take it! Glad to hear you enjoyed it.
Thank youuuuu... I've learnt and relearnt P&S so many times that it's embarrassing. Even 3b1b didn't help beyond a point. You're a world saviour!
This is so helpful. I'm struggling with understanding distributions and your videos showed up. What a bless! Looking forward for your next videos!
I usually never comment on UA-cam videos, but damn your videos are great! I have a course on Markov Processes right now, and this video just sums up distributions so nicely. Def earned a sub, bro! Keep up the great work
Much appreciated! Happy to have you
Very cool example with the graph edge distribution!! Awesome video!
Thank you!
Really useful video! It's hard to find this kind of content on UA-cam.
You are the best!!!! This channel and 3B1B are saving me. Keep it up!!!
Such a very insightful video that not many people talk about on different probability distributions. Thank you.
Thanks Tim. This is an old fav of me
Amazing video! Please share even more insights into distributions! I have such a hard time understanding the intuition of many distributions. Like when to model data with which distribution? I study robotics, and usually, you can get away with calling every random variable normally distributed, but that's because of some engineering laziness. You surprised me at the beginning with the great intuitive angle and I would like to see more if you have some.
This video is a good place to start. If you ever do a bit of "Probabilistic Programming", it forces you to think like that real fast. And then you discover that there's only a handful of distribution that get used a lot. The normal, the uniform, the beta, multinomial, cauchy, half-cauchy, ... and the reasons for choosing each are pretty simple. "OK this one needs to be always positive which is evenly distributed over a log scale".. stuff like that. It's certainly a learnable skill
This was really illuminating! Quickly becoming a fan of your videos. Keep it up!
Where were you when I was learning probably distributions. WOW. GOD bless 🙏🙏🙏
DJ clarity is crystal clear. zero defect. six sigma.
the graphic was epic indeed, and the support will continue indeed !
i like the idea of demystifying probabilities and statistics which are such great tools and ways of seeing things.
to bounce back on some of the things said in the comments:
- i noticed the light changed a lot during the footage, especially around 1'30. not a big deal for me, but an idea to increase the quality.
- you sometimes speak very fast which might be a bit hard for non-English-speaker viewers. maybe this is a tough point to improve rapidly. as long as you are comfortable and clear, it fits for me.
see ya ;-)
Thank you for the feedback - I really do need it to improve.
Regarding the light, I know! The backlighting shows up sometimes and I only discover it in editing. I'm going to experiment with black out curtains, to make the lighting more consistent.
Regarding the fast talking, this is a bit of a stylistic choice - I like the high information density it brings. At the same time, I don't want to alienate non-English-speakers. The solution I know I need to do is to get accurate subtitles. Hopefully that get me partially there.
Thanks again, I hope to keep you watching!
Thank you for you video! Your are very talented into explaining
Awesome Job!The best distribution video!👍👍
I was working on lottery probability. I was thinking about Binomial Distribution but in the movie Jerry and Marge Go Large , Jerry said there are two factors such as Human errors and the time buying tickets, any thoughts?
Randomly stumbled upon this excellent vid
Welcome!
maestro, me paro de manos y aplaudo con los pies.
Poisson distribution is not the continuous version of Binomial. The continuous for Binomial is the normal distribution. PS. Amazing content. I'm subed and belled.
I’m curious about the book on the table, I can only decipher „All of Statistics“. Is it the Wassermann book? Do you recommend it?
Yep, "All of Statistics" by Wasserman. Excellent book covering fundamental stats. It's dense with information, but not terribly hard because it's not too abstract (e.g. very little measure theory) and he does a good job keeping motivating examples front and center. I definitely recommend it, especially parts I and II. In Part III, he starts talking about specific models and I think that topic is better covered elsewhere (Elements of Statistical Learning, for example).
Subscribed! My background in statistics is limited to AP Statistics in high school and an amateur interest in forecasting (in the spirit of Philip Tetlock's Superforecasting). I loved this video, but I have a lot to learn to understand all of it. I'd love to hear what wisdom you have on what probability distributions are most commonly found in the world in general? Specifically, probability distributions that show up when looking at the distribution of events that occur in the real world, geopolitics, technology, etc. Maybe there's not a good answer to this question, but figured I'd ask. :)
It's a good question. What you find out is that it's the exception, not the rule, that some known simple density fits the data well. More often than not, you need to use large mixtures of distributions to fit complex real world phenomenon. When you start dealing with super huge numbers and very simple processes (e.g. the counts of clicks on hugely viewed advertisement), then you can may find simple distributes work well. But often, we're not so lucky
@@Mutual_Information Thank you for the reply!
@@WilliamKiely In the systems simulation world, it's pretty commonly acknowledged that most queuing service times are almost always some form of lognormal-like distribution, and arrival processes are some form of (generally nonstationary) Poisson distribution. These are the two 'big' ones in my experience.
@@NemisCassander Interesting, thanks!
Interesting channel well presented - It would be good to tie in the general description to its application specifically in investing. Education without application is just interest.
Funny thing I've surveyed the audience - they are all here just for interest! Which is a bit.. not my aim. This is supposed to be application-ready material, but UA-cam just isn't the go-to for that. Hm
Great video and great recommendation. It almost feels like a cheat, even though it sounds intuitive. Though, unfortunately, most stats/ML books do not put in this nice story-form at all, not even in statements. Which makes these videos unique and absolutely life savers for many ML savvies out there. Thank you!
Thanks Ammar - glad it helps :)
The austrailian teacher Tatum, in visualizing math, great courses, this guy reminds me of him.
This is great! I was wondering if there is a complete 'taxonomy' of statistical distributions.... I bet it's not possible because of Gödel's Incompleteness Theorem... but I don't know how to prove it.
That's huge diagram is the closest thing to it. It was quite a project for the authors.
That was really insightful
great job! that s nth degree anaylisis. Humbling and rich!
Perhaps this could be placed in a "Statistics&Probability" playlist? Some people watch videos by playlist. Also, you could perhaps make UA-cam shorts from your videos...I heard it helps boost the algorithm. Thank you for the videos.
Interesting idea. I just gave it a look and I'm not sure where to find such a playlist, but if you know of one (or anyone else possibly reading this comment), I'd love to find this video on that list. Thanks for the idea
And funny you mention it, I just created my first short a few days ago!
@@Mutual_Information I mean the video should be added to a "Statistics" playlist created by you (on your channel), as it helps to categorise your videos and makes such videos easy to find. Only if it's convenient for you of course.
Thanks for taking our opinions into consideration.
Why wouldnt the normal distribution be the analog to the binomial distribution instead the poisson distribution?
Yea there is a relationship there as well. The normal is another distribution you can reach by taking a limit of the binomial. But the Poisson is also one you can reach with a different limit. I just didn’t cover the normal here directly.
Amazing job! Keep it up
Excellent Intuition
i try!
Great intro
Awesome video
is it the case that there are fewer discrete distributions than continuous? I was thinking that there would be a one to one.... but I think there are some continuous that are built on top of other continuous, so the total number of continuous is more than the discrete..
That is an interesting question.. and I can't even pretend to know the answer
I'm not sure that there are more continuous distributions than discrete distributions in actual fact, but I can say with some confidence that more continuous distributions are _used_ in numerical operations than discrete distributions. One reason why is that it is often simpler to generate variates from continuous distributions than discrete distributions.
You are God of visualization. Thank you 🙏
I have a question, are you know a family of distubtions when value of observation depend on parameter?
For example: Pareto, Uniform, two-parameter exponential and so on, into one family distribution based on order statistic (first and last).
Hm, if I understand what you're saying, you're asking for a family of distributions which contains all of those? I don't believe there is one. Distributions where the support varies can be tricky to generalize.. if there is one, I haven't heard of it.
Great video man, but as a student of statistics currently in the second year of my undergrad degree, I still don't know how the eternally beautiful Normal distribution came about ... Sure it has fascinating and elegant properties (shoutout to CLT!), but where did it originally come from? Can you maybe shed some light on it, or suggest some resources which I could lookup????
Explaining all that is.. quite a challenge. 'But what is the CLT' by 3Blue1Brown is about as good as I can imagine you'll find out there. But maybe you already knew about it!
@@Mutual_Information Yes, and truly that is one of the great expositions on this topic, it made a lot of things clear. But still, as you mention in this video, is there a related "story" from where the Gaussian curve just pops out naturally? Like it's a pretty complicated function and I think it cannot be trial and error alone to determine that beast ... 3B1B does provide some insight though, I am just annoyingly more curious 😅
@@ShubhronilDutta If you’re interested in the history, I believe that it was originally developed by Abraham de Moivre in the interest of approximating the binomial distribution for large n (using a different limiting case than the Poisson process). There are also various stories about how Gauss “discovered” it empirically in naturally arising data. De Moivre’s route is the more “elementary” one, but the derivation is surprisingly long and annoying. There are some more modern approaches to deriving the Gaussian as a limiting case of the binomial which use more heavy machinery (such as Stirling’s formula) but result in a simpler path.
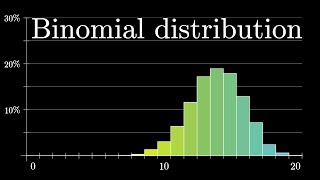
Isn’t poisson a discrete distribution? 5:27
Excellent video! Thanks
Thank you!
Is there some connection in how those distributions arising from counting Bernoulli trials are all maximum entropy distribution under slightly different information? This might be a trivial observation or irrelevant and I’m not sure which lol
I think it must be there, but I’m not sure I see it clearly. Sounds like we both understand the principle of max entropy.. but I don’t think I can draw a straight line to the counting process I’m showing here. 🤔
@@Mutual_Information Oh man this responses makes me feel better that it wasnt obvious one way or the other to me! Now I just want to research this a bit more 😈 It feels like because entropy is like how many binary decisions do I need to make on average - given certain conditions - to get a decided answer must relate to counting series of binary outcomes in different ways...
Thank you
This is a very useful video. Thanks a lot for that. I am trying to figure out the relation between Statistics and Machine Learning. Can you suggest a beginner's book? I want to relate the distributions as explained here to the Machine Learning Algorithms.
I’d say ML uses statistics a lot, and that usage is varied. So it’s hard to say anything about “the” relation, since there are many usages. For a beginners book on this, I’d suggest “An Introduction to Statistical Learning” by Hastie and others. It’s a very statistically oriented view of ML.
As someone who unnecessarily struggled a lot in the subject, it makes me GENUINELY angry that this isn't the FIRST lecture for every probability/statistics class.
Well I'm glad you saw it eventually!
What's your favourite story for the Beta distro :)?
I scratched my head on this one. I do not know of a good generative story for the beta distribution, but it's certainly part of one. If you model the theta parameter of the binomial distribution with a beta distribution, you get the beta-binomial distribution. This is useful for modeling things like.. if one product has 10 positive reviews and 1 negative reviews.. is that better or worse than another product with 90 positive reviews and 15 negative reviews? A question like that shows up a lot
@@Mutual_Information I've been on my own journey over the past few years to try to distill some of the most foundational distributions into their properties that can be distilled from first principles. The beta is still one that I'm struggling with. If you check out the Wikipedia page (en.wikipedia.org/wiki/Beta_distribution#Random_variate_generation), there's an interesting Poly urn generating process and a route through order statistics, along with less-motivated processes involving gamma functions. I agree that the "simplest" way to derive this is in looking for a conjugate prior for the Bernoulli process and "guessing" that the distribution is proportional to (1-x)^a*x^b (following the non-normalizing portions of the relevant PMFs). The beta distribution immediately pops out from this given that you have support on [0, 1], and it also explains why all the Bernoulli process distributions share a conjugate prior.
Interestingly, the beta function was originally developed in the context of the gamma function and analytic continuations of the factorial function, so I've been going down a rabbit hole in that direction. I figure the more motivating context you have, the better understanding you'll have and the more you'll be able to fool yourself into thinking "I could have come up with that!" 😂
You are genius!
Amazing Video!! Added one more Excellent UA-cam channel to my subscription 😊
Thank you very much! Glad to have you
grt work sir
Awesome!
Poisson is a discrete distribution
Dam, this video fills in a GAP...
Any chance these could be simulated in R? (Love to se it)
I'm sorry, but isn't poisson distribution a discrete one?
Yes, in what 'discrete' and 'continuous' typically mean. In this case, I was using them to mean something different. I was referring to the building block used to construct them. So in this case, I call Poisson continuous because it's a sum over continuous things. I.e. it's counting up exponential samples over certain ranges.
Some constructive criticism: from 2:44 onwards I kinda lost you and what you were talking about... Maybe explain what you're plotting, where you're plotting it, and why.
Thank you Krishna, constructive criticism is what I need right. I agree that I have this wordiness/static frame problem and it makes zoning out too easy. I certainly do it myself when I’m recording. I’ll work on it! And thank you for helping - it means a lot.
@@Mutual_Information That is not what they are saying; you didn't explain how you got the values to throw on your plot...
@@caleb7799 it’s a probability mass function. I assume the audience is familiar with certain concepts. I’m not teaching what a distribution is, but how distributions are related.
your beginning monologue would save the world alot of pain if it was applied universally
I am here again as I miss very much.
content is pretty good, somehow the video quality is lacking
What are you seeing in particular? Low resolution? Is it the resolution of the giant graphic with all those edges?
@@Mutual_Information no, I was referring to the camera footage. I have it at 1080p60 but I think it's slightly blurry or has slight granular noise. Actually, it reminds me of colour compression. If I look at areas that should be unicolour I can see slight shades. It could be my monitor to some extend (I'm actually getting a new one) but if I compare side by side with e.g. DIY Perks I feel like I see a difference.
Maybe it is more obvious if you compare what is black in the graphics vs what is supposed to be black in the camera footage.
@@aBigBadWolf I know there was some color correction involved, but the parameters of that aren't always selected in the same way. There's a similar story for the sound. I'll compare those parameters to other videos. And thanks - I appreciate the feedback!
Well, I'm subscriber nr 53. Onwards, I say!
❤
!!!!!
You like learning about math sister!?
love it.
I am a fellow DJ how do today?♓
Friendly Greetings, HMU
We are few and far between. Welcome!
Started of good, then ran into the woods…
Politicking science.
Co-she. Great video.
yeah my brain broke
At least it's good exercise
lost me at the beginning....
😂
Thanks!
Thank you Mason! :)
Thank you
Thank you!
no problem ;)