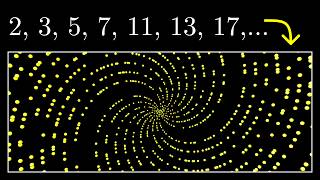
Prime Spirals - Numberphile
Вставка
- Опубліковано 10 лют 2025
- Prime numbers, Ulam Spirals and other cool numbery stuff with Dr James Grime.
More links & stuff in full description below ↓↓↓
James Clewett on spirals at: • 41 and more Ulam's Spi...
And more to come soon...
subscribing to numberphile does not really change your physical appearance!
And "golden line" in this context was made up by Brady!
NUMBERPHILE
Website: www.numberphile...
Numberphile on Facebook: / numberphile
Numberphile tweets: / numberphile
Subscribe: bit.ly/Numberph...
Videos by Brady Haran
Patreon: / numberphile
Brady's videos subreddit: / bradyharan
Brady's latest videos across all channels: www.bradyharanb...
Sign up for (occasional) emails: eepurl.com/YdjL9
Numberphile T-Shirts: teespring.com/...
Other merchandise: store.dftba.co...






![Lp. Сердце Вселенной #60 РОЖДЕНИЕ ЛОЛОЛОШКИ [Финал] • Майнкрафт](http://i.ytimg.com/vi/YoR0pAV9FVQ/mqdefault.jpg)

I love his smile while talking about mathematics.
That's a person who's loving the thing he's doing.
And so proper. Makes what he does interesting.(even though I feel like a prime idiot after ) lol
James is the best.
He is very fortunate. Most people can't do their hobby as a job.
@@cube2fox Yeah, some of us are born in the wrong set of square kilometres to be doing math
“NOOMBAHS”
Every once in a while, I come back to these numberphile videos to just listen to James Grime talk about his numbers. It just makes me feel so happy that he exists and that he's doing something he absolutely loves.
I could never do what he does, but his enthusiasm and passion is inspiring:)
New primes, bigger primes, optimus primes
+Dylan Le Lerre
One day we'll find one. One day...
To find infinitely many numbers divisible only by themselves and 1 is the right of ALL sentient beings!
It isn't ment like that
James Grimes.
James Grime Smiles
1:18 Ulam was bored by a lecture and was doodling. I like him.
Three years later, I still like him.
@@314rft 3 weeks later, I agree.
@@marios1861 3 weeks later (again), I also agree
@VladHPsuper Gaming 9 minutes later, I also do nothing
star of duty 1 week later, I question the number sequence of the UA-cam algorithm bringing the comment, and it's video, into our knowledge within short periods. On an old af video.
We've dug too deep
The matrix is being unveiled
+Felipe Palma
You don't want to meet the Architect.
+Sassymui8 Rumor is, he is a smelly neckbeard
+Sassymui8 You mean The Oracle.
+Curran Hyde we delved too greedily and too deep
Which pill will you take?
James showing his true 'attraction' for primes
"Look at these curves."
lol
the 26th lol
@@genericusername4206 lol
That’s why the channel’s called numberphile
@@subzeroelectronics3022 I don't think you get the joke...
thank you
You’re very welcome
What I most like about numberphile is that they put subtitles in every single video. I really appreciate that ;D
Sad that he's name isn't James Prime.
Let's start a petition to make him change his name.
Magnus Seidenfaden Well, rather "Pierwszy"
+ Noel G.
No, all we have to do is define some special kind of prime and call it a "grime."
Like, maybe if it's gritty enough . . .
his*
he's number one
Like Ulam I was bored in my Math class a while ago and eventually wrote a Java program to generate his spiral. I found it really interesting to add color based on the relationships between the primes, like twin primes, primes that are 4 apart, 6 apart, and so on.
You guys never cease to amaze me. You make even the most complex concepts in mathematics seems really easy. Keep up the great work guys :)
keep an eye out for brown papers on ebay... I'll put this one up some time... best thing is to follow numberphile on twitter and facebook! :)
This is amazing.
I thought they were all randomly spread out.
I knew you can use find out the density of primes but not find patterns such as this.
Beautiful.
sometimes i go back to videos on this channel because it's always fun, and... wow. i didn't remember vihart getting a mention here 10 years ago.
Very interesting video. Many years ago, when taking a Number Theory course in graduate school, I mapped the integers onto a spiraling lattice and noticed that the twin primes tended to be found at the edges of the lattice. [This property of twin primes being at the edges only worked for the first few dozen twins.] I developed a crude recursive formula, but didn't have time to pursue the study. Years later, I noted that Stanislaw Ulam had discovered this and developed it at least a decade earlier. During the mid-60s, Scientific American had an article on Ulam's remarkable work.
I like this guy, he's really excited about the primes
You've got to love that ViHart reference😜
ViHart FTW
UA-cam *DID NOT EXIST* back then. LOL
Was great reference
oh yeah. I heard "Ulam" and was like, "now where have I heard of him before"
@@firefish111 LOL
Writing a number line in a hexagonal style produces some pretty interesting spirals as well. All primes fall on one of two axes, either the 1st, or 5th axis, and you can see where the multiples of inner numbers will "block" because of the patterns of every multiple of every number crossing on to either axis. -Where any multiple of any number crosses the 1st or 5 axis, there will be no prime. Also it's pretty to stare at lol. ((1-6 for the first ring, then 7-12 for the 2nd ring 13-18 for the 3rd ring. -with 7 above 1, 8 above the 2nd side, 9 above the 3rd, 10 above the 4rth side, 11 above 5, 12 over 6, 13 above 7 in the 1st column, 14 above 8 in the 2nd column .... ect.....)) You can see clearly where n mod 6 = 1, and also when n mod 6 = 5. :)
"Look at these cuuuurves" :D
I love how this is used for once in a nonsexual way
Thank you Dr. Grime and Brady for bringing us these videos. By the way, Dr. Grime you are my favorite.
Half the diagonals have only even numbers, so only the diagonals with odd numbers have any prime numbers at all, with the exception of those that go through the number 2.
Pause the video at 4:10
You would notice that the length of sides of all the spirals are odd.
Therefore almost all of the corner numbers are odd, making them most likely to be prime numbers.
Also note that every alternate vertical and horizontal number is even, making it almost impossible to form any vertical/horizontal prime line.
Seriously Brady, thank you so much for this channel. I love it.
Ulam's Square produces the appearance of diagonal runs of primes because primes (other than 2) have to be odd and the odd numbers are restricted to a checkerboard pattern. If you run a random number comparison with that same checkerboard restriction in place (which Numberphile didn't do), then the randomized square will produce a similar appearance of diagonal runs. This is likely true for the spiral in the latter half as well, where I'd bet the "curves" come from the layout of even and odd numbers, and the "prime curves" are just artifacts of the even/odd curves.
Note: While the whole even/odd checkerboard for the square is pretty obvious, I actually did bother to run some tests just to confirm it. I ran multiple tests on increasing size squares. Every test where the hits were restricted to a checkerboard resulted in the appearance of "diagonal runs" of hits.
Always amazes me when many new things are discovered at unusual times in unusual circumstances. Some of the most productive work happens not through a tight academic schedule, but through simply playing, exploring, letting the mind wander etc.
This and your other video inspired me to break out my TI-83 and do some programming! Unfortunately I can only plot a 94x94 spiral and it takes about 10 minutes for my poor calculator to do, but it's still pretty fun. I plan to see if the odd-only primes idea really does completely account for the diagonals.
If you Pause the video at 4:10
You would notice that the length of sides of all the spirals are odd.
Therefore almost all of the corner numbers are odd, making them most likely to be prime numbers.
Also note that every alternate vertical and horizontal number is even, making it almost impossible to form any vertical/horizontal prime line.
Also, you cannot predict any prime number using this pattern, because we do not know when the diagonal line is going to start and end.
They are just trying to force a pattern on prime numbers by arranging them in some way, but since primes themselves do not follow any pattern they break diagonals in between. Because, not only just EVEN numbers are non-primes, other ODD numbers such as multiples of 3 after 3, multiples of 5 after 5, Multiples of 7 after 7 (and so on...) are also non-primes, which breaks the diagonals in between.
Nice thinking!
How to make a great mathematical discovery: doodle in math class
The story of the Ulams spiral is written in my book of maths of high school, so I get interested,
I knew I would find a video of Numberphile, and you guys told exactly the same story, but even better ! props for that my dudes
After seeing this I was curious about other spirally shapes, so I wrote a quick java program to generate a 1001x1001 grid of a rhombus shape like this:
7
... 6 2 8
13 5 1 3 9
12 4 10
11
...and the result is rather astounding! You can see clear horizontal lines of prime numbers (but not many vertical), some of which seem to carry on for very long without much interference. Link to picture in first reply (I think some people block comments with links in them so it's best to have it separate)
Omg primes are like busses, I like that a lot.
3:14 (PI!!!) are those random odd integers with natural log variance?? or just random pick of all pos. integers?
I would guess probably the same variance as the average gap between the primes which as you Said is approximately log n
Bengt Bengt we guess but we dont know what he did :(
nope :)
Brady, you are a legend
The Sacks Spiral looks like iron filings on paper over a magnet.
I literally watched this video at the same time the follow up vid was posted. It was a rather pleasant surprise.
I don't even see the code, all I see is blonde, brunette, redhead...
What a reference. What a film.
lol
I mean....props for this
Whoa, that 4x^2 - 2x + 1 works for x = -1 as well, you start getting the other end of the diagonal. I wasn't expecting that.
very cool.
very cool comment.
very cool reply.
very cool minds of math we all have...
i just absolutely adore this guy
would using a different base reveal a pattern to? perhaps even clearer?
Would a different base change the design? Primes come in the same order in all bases, or so I believe.
bases dont matter? primes are number that are defined using other numbers, none of which has anything to do with bases
You would really love this book. I did. Peter Plichta illustrates how the prime numbers are ordered on concentric circles numbered 1 to 24 and then 25 to 48 and so on; expanding outward like cross shaped rays of sunlight radiating outward. The guy was a genius!
I'd like to see the positions of the twin primes on those diagrams. Edit: Oh, and I wonder if there's a way to arrange the numbers in another dimension to create similar patterns.
Yea.. I was thinking the fibonacci spiral...
That's no spiral, that's a space station!
What happens if you do an ulam spiral, but instead of circling primes, you circle random odd numbers with logarithmic spacing?
+TheFizzyKerbal That was my first thought: oddity would be enough to explain that pattern?
+Aviel Menter ok
+Augusto De Nardin ok
+Aviel Menter This is additional information about the patterns seen:
The diagonal lines in the Ulam Spiral are the result of the pattern you get when you plot out the position of all numbers in the set "6n +/- 1". All prime numbers except for 2 and 3 are in this set ... it's the set of all odd numbers that aren't a multiple of "3".
The "6n +/- 1" set makes an especially elegant pattern of diamond tiles when you seed the number spiral with "0" instead of "1". Seeding with "1" results in the same field of tiles, but with an ugly seam near the diagonal line containing the squares of all odd numbers. I'm not sure what effect seeding with "0" would have on the "rich veins" of diagonal lines.
Christopher Night Thank you!
He looks so happy talking about these things, and I can totally relate to that.
Amazing! And 7:00 looks like a basketball!
Ace Diamond lol. I initially thought that it looked like the Death Star
Great question. I suspect that when we're looking for one thing, we often find other stuff that is useful, even if we never find the thing we set out looking for in the first place. This is also why it's important to day-dream and doodle.
Do "rich veins" of primes on the diagonals ever peter out? Do new ones pop into existence farther from the origin? As I mentioned in my last post, the skeleton of this pattern is a very regular network of diagonal lines, so the number of "golden lines" is quite sparse in comparison. Could these be "coincidence eruptions", like the rogue waves that sailors fear on the open ocean?
+Len Arends Thats a really interesting question. thanks.
+Len Arends One quadratic that always has a high prime density (but doesn't form one of those lines) is x^2+x+41.
Correction: Euler's formula that I mentioned does eventually get on such a line.
The opening of this was beautifully edited. It was cut off perfectly.
What happens when you make an Ulam Spiral in 3d rather than 2d?
piynubbunyip 2 yrs but anyway imagine in what direction should it go.
wo997 +1 more yrs, there is no way to make a spiral in 3d with counting numbers being next to each other in a formatted pattern.
There's then another dimension of posibilities of patterns when doing so
Well you could make an helix
You get an Ulam Meatball
i love this channel, amazingly simple and pleasant to watch.
***** shoutout @1:23;) Well done.
gotta love James Prime
what if you just visualize random odd numbers on the spiral instead of all numbers for the random pattern? numbers in a spiral like this show up as a checker pattern of even and odd.
so?
yeah and what about making a spiral from only odd numbers to see if the primes still arrive at any such patterns... well spotted guy
That's exactly what I thought
That does leave you with the awkward question of what to do with your initial prime number of 2
well yes you would see some rough patterns like in the video still, but you know why, because the primes end in 3's 7's and 9's! christ the more you think about the above video the more it looks like an april fools prank gone subtle
Did anyone else notice that the squares of all even numbers lie in the same diagonal line
Of course it is concentrated into diagonals, the even values would prevent any other pattern from obviously showing up well at anything other than 45 degree angle.
Clinton Johnson but some diagonals have more primes than others all diagonals only contain odd numbers but not all have as many primes as each other
David Steere Exactly. It's not that they're concentrated into diagonals. They are concentrated at CERTAIN diagonals, which is the point to begin with.
I love the way you say Stanisław.
Watching this after seeing the 3b1b s' new upload
Yep, me too
🙃
1:17 I love how happy he is while saying “very boring lecture”.
Is there a pattern of primes by doing the same thing for Fibonacci numbers (1,1,2,3...) instead of counting numbers (1,2,3,4...)?
No 8 is not prime but in fibanachi
Fibonacci is literally spelled correctly in the comment. couldn't you look and see how it's spelled? also, that's not what they meant. it doesn't matter if it's prime or not, you're just going to circle it if it is.
Vigo Hornblower the Fibonacci sequence is the most overrated sequence ever
@@corinth6402 Your reply is math version of r/whoosh
I don't know how many fibonacci numbers are actually prime. Don't forget they blow up in size quickly, on average becoming larger by a factor of the golden ratio with every term. It would be VERY sparse very quickly as the size of the numbers grows exponentially as you get away from the origin. There may actually only be finitely many fibonacci numbers that are prime, this would not surprise me.
In case you are serious: they will look identical; prime numbers are the same in any base.
Division operations don't change when changing the base so when a number is only divisible by 1 and itself in base 10, it remains so in any other base as well.
Therefore, if you place numbers in another base on the spirals, the primes will remain on the same spot.
0:58 - Kudos for pronouncing Stanisław right, with "ł" not "l".
@᪶ ᪶ Polish "ł" is very close to English "w" in "we" or "wet". Polish "w" sounds like English "v".
Huge respect for the correct pronunciation of his name.
7:06
This is how Death Star was invented.
i thought it was a basketball
That movie would've sucked then LOL :p
Oh thank god I thought I was gonna have to say it
I love how the primes graphed along the Archaemedian spiral result in figures that resemble logarithmic graph functions.
1:24 ViHart reference!!! "Triangle!"
This is incredible.
Curious if there are any other types of spirals that show other interesting patterns when filled in with primes
A similar concept I came up with while doodling in school too...
Get grid paper, and do rows, draw lines through primes; they line up at various different angles
Brady can you ask them if the
This Great and straightforward; when you read about Ulam spiral in Wikipedia they make it seems very complicated !
Kind of frustrating! Seems like there's a pattern in how prime numbers are spaced but nobody's figured out a formula to predict them yet, and I'm sure that really clever people have been trying since Euclid's day.
Then again, calculus came over 2000 years after Euclid and that opened up a whole new world of mathematical possibilities (and it's something that a high school student can grasp). Maybe, in time, we'll have a whole new way of thinking about math that will make this prime number mystery seem trivial.
maybe calculus is taught in high school because of it's myriad of uses and not because it is easy to grasp. It's one of those subject that comes straight out of philosophy so I can see why it took so long to develop properly...
Absolutely!
I just have a hunch that there is a shape that would hold the lines constant, but that we don't know what that is yet.
Who came here after 3Blue1Brown's video?
Franz Louis Cesista yeah, just watched it
🖐
+1
Me
Not me... I searched on UA-cam for ulam spiral and this came up
James Prime demonstrating Grime numbers!! Yay!
Hi, there, is there anyone who tried to arrange numbers into a three dimensional cube, instead of a two-dimensional square?
How exactly would you do that?
There are only 2 alternatives: a conical spiral and a cylindrical one, because it's very hard to make a 1D line move like a spiral that touches all numbers inside a cube and progressively does the same thing with larger cubes using the 1st cube as the center. That's why the trivial alternatives are either a cylinder or a vortex wrapping a finite sized cube, instead of an infinite sized cube
The story of Ulam creating this spiral really struck me because I remember in 8th grade I was stuck in a very boring something or other and drew this kind of spiral, highlighting all the primes, and then gave up deciding it wasn't anything
what if you use a hexagonal spiral, or not a spiral at all, what if you add in negative numbers?
I got an almost completely awesome result when I started with 43 on a square grid and spiraled in the same direction as the vid but numerically downwards as I moved outwards, getting to 0 then -1 -2 and so on. I ended up with a long unbroken prime diagonal starting with -229 in the southwest and -607 in the northeast. Though I guess this implies accepting 1 as a prime (or at least non-composite), and 13 and -13 as distinct primes. Watch this space for hex spirals.
"Numbery stuff" is a great definition of the occurrence of probability primes.
7:06 OMG It's a death star
7 years late, but I was looking for this comment!
You guys are amazing. Thanks.
Let's build Prime Maps!
I emailed this to my math teacher. he was impressed.
7:08 Pacman ^^
thanks
Still not convinced by the pattern in this video. The comparison is made to random numbers, but primes are certainly odd (except 2), and all odd numbers are on diagonals. So isn't it normal we see diagonals when the picture is part of a picture with only diagonals?
I'm not saying this is all false btw, but it would have been nicer to show the difference between the prime numbers and random odd numbers, instead of random numbers without any restriction.
+Sander Deryckere I saw someone do that. The same patterns don't emerge. There is something special about prime numbers. A lot of mathematicians have thought about the Ulam Spiral. If it was something as simple as it being odd numbers, it would have been discovered.
+Houshalter As I said, I didn't claim this video to be wrong, I just claim this video to be not convincing enough as it was presented here.
+Sander Deryckere That's a slippery road if you ask me. When you graph random odd numbers, it isn't completely random anymore : you have introduced a bias.
Then why stop at eliminating numbers divisible by 2 ? Why not eliminate the numbers divisible by 3 ? Primes are never divisible by 3 so that would be a better comparison. Then why not add the numbers divisible by 5 ? And 7 ? And so on.. By eliminating more and more divisors, you'll end up with the graph of prime numbers, with the same pattern shown in this video (or at least a subset of it, keeping in mind we pick inside it at random).
Surely the pattern will start to emerge somewhere along the way between complete randomness and your elimination by divisors process. Therefore some faint properties of the pattern should be visible in earlier iterations, like the graph of random odd numbers. So I think comparing to completely random numbers is more relevant.
+mens sana but it's easy to show that there's a relation between diagonals and oddness of a number. It's not the case for multiples of 3.
And if you see the same pattern for whatever multiples you leave out, did you really find a pattern for prime numbers then?
There are more patterns I could find for prime numbers. Like patterns in the final digit of a number (which almost never even or 5). But would you classify that as a pattern for prime numbers, or as a pattern for multiples of 2 and 5?
Again, I'm not saying this video is false, and there are probably statistical methods to see if there's a pattern there or not. But as it is, it's not very convincing to me.
mens sana Randomness doesn’t implies equality distribution nor lack of any pattern , you know nothing about basic statistics.
The Sachs spiral looks like a combination of a basketball and a Death Star. I like it.
ive ventured into the deep and dark world of intense boredom
Massive Balloonknot 1.49 AM
How are prime numbers boring
I first heard of this when I was 12. I said "but they look like a garden"! And yes, a lot of French garden designs look just like that.
Am I the only one who thinks this is hiding a depth so complex that we can't comprehend it and finding it creepy as hell? Yeah? Okay...
That narrows it down a little bit, but not enough to close the book on the Ulam spiral. The interesting part of the pattern is that some odd diagonals have few primes, while others have many.
Quick question: When we would make this spiral with the number base of 12 instead of our base 10 system, would there be patterns and when yes how woud they look?
I'm really interested if those patterns are connected to the way the universe is or only to the way our base 10 counting system is
Magnus exactly what I thought.
George Lubomirov When I get time I'm going to make a base 12 spiral and post it here for you
It's not going to make a difference. The only thing writing a number in a different base does is change how it is written. The values are still the same, regardless of how you right it, so there will be no difference in the pattern.
Yeah, after a bit of googling I understood that :)
I learn so much from just watching 30 seconds of numberphile
The plural of formala is formulAE and not formulAS!
formala is the plural of formalin.
You are gAE
Not if the world "formula" gas been absorbed in english
Prime numbers are located on equations all over Ulam's Spiral with this form 4x² + ax (a is a whole number). A lot of these equations are 45 degrees diagonals on Ulam's Spiral while others have other angles (at least at some parts). It is obvious that all non prime numbers are placed on these diagonals. Therefore prime numbers on Ulam's Spiral are just the holes left by the drawing of all those equations.
I think its obvious that these spirals occur....
every prime is represented as 6k+(or-)1
so primes can't be everywhere unlike his "random" example..
2=6k+-1 ?
@@VikeingBlade excluding 2 and 3
This is silently blowing my mind.
mommy im scared
great explanation by James.. I hope I'm not wrong with his name.... Even a tiny matter ll be explained.... Great teacher.... his students ll be more benefited.... thanku for ur struggle to create a topic and study it and explain in very simple manner....
Amazing ! You remind me some of my discussions about prime numbers with a dear friend of mine when we were at high-school.
If you start with some other configuration, you also get lines of prime numbers like in the ulam spiral.
For example, if you make the Ulam spiral, but start with 0 instead of one, you will get diagonals of primes., which is especially interesting because the graph itself (in terms of what numbers surrounds other numbers) can be very different than the Ulam spiral, especially as you go farther out.