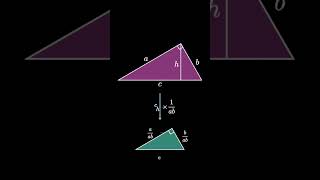
Regular dodecagon area (visual proof without words)
Вставка
- Опубліковано 6 тра 2023
- This is a short, animated visual proof demonstrating that the area of a regular dodecagon inscribed in the unit circle has an area of exactly 3.
If you like this video, consider subscribing to the channel or consider buying me a coffee: www.buymeacoffee.com/VisualPr.... Thanks!
This animation is based on a proof by Roger B. Nelsen from the January 2015 issue of The College Mathematics Journal page 10 (doi.org/10.4169/college.math.... ).
After I created this, I found another wonderful animation of this same visual proof : • Area of dodecagon | Be... (though the animator there does not cite the original visual proof from Nelsen).
#math #manim #visualproof #mathvideo #geometry #mathshorts #geometry #mtbos #animation #theorem #pww #proofwithoutwords #proof #iteachmath #dodecagon #area #dissection
To learn more about animating with manim, check out:
manim.community








Wow, this method is even better than the short making a square with side length √3, since it doesn't use Pythagoras.
And that was already one of my favourite videos!
How do you compare it to the third version : Area of a dodecagon
ua-cam.com/users/shortsuxL7K2IZBf8?feature=share
@@MathVisualProofs
Quite a difficult comparison.
From a regular viewer's perspective, I definitely like the symmetry of this proof and the fact that the pieces feel simpler.
But the version in the link sets a clear goal, making the proof easier to follow.
As for rigour:
The version in the link is way less rigorous, because the fits aren't obvious.
This proof has every length very clearly as either 1 or x. The construction follows simply from SSS similarity.
@@caspermadlener4191 love the thought you’ve put into this!
@@MathVisualProofsthe linked video is private
@@VishramKidPG123 thanks. Made alternate version: ua-cam.com/users/shortsuxL7K2IZBf8?feature=share
There's also something kind of neat about the dodecagon being cut into 12 pieces, and the squares each being made of 4 pieces
This is why the formula for the area of a circle is (pi)(r)^2. Because pi is very close to 3r^2 which is how you find the area of this shape!!!! So cool!!!
Wow, this is really well done. Thank you for this gem
We might not be able to square the circle, but at least we can cube the regular dodecahedron 🤷♂️
Another lovely visualization explicated
Wait so does that mean the generic formula is 3r^2?
no, that's just for the regular dodecagon inscribed in a circle
Yes!
@@walter7825 Well, literally every dodecagon can be inscribed in a circle. So yes, this is the formula for the area of a dodecagon.
@@wanderinwolf3804 i meant to say that the formula works for a regular dodecagon only, also not every dodecagon can be inscribed in a circle
@@walter7825 true! Only regular decagons can be inscribed in a circle..
Umbrella ?
Would you ever consider doing a visual representation of Laplace transformations? Perhaps illustrating it in the context of Routh-Hurwitz stability criterion?
I second this
Wow😍
Let me just mention the channel "Think twice" here, they also did this proof a few years ago in a similar style
It’s in the description :) they didn’t link the original source though.
@@MathVisualProofs Maybe that's on me, but I don't think I can see your description here 👀
@@pengin6035 You should be able to. But it is not obvious in shorts. You have to click the three vertical dots in the upper right corner next to the camera icon and then you can click the description. It's one of the many things I dislike about shorts because I try to be pretty careful about providing attribution if at all possible, but I am sure most people don't know how to find the description for shorts... so no worries :) I do like that version by ThinkTwice
@@MathVisualProofs Oh I knew that and I did that, but for me it is empty. But I also dislike this about shorts, you're not alone 😅
However it seems like this is a bug in UA-cam, I can't see any shorts descriptions. Weird, but nothing wrong on your side :D
@@pengin6035 Oh geez. Sorry. It seems to be there for, me, but I will try to use some other device to see. I appreciate it (and sorry to explain something you knew :) ).
Good, a visual proof that is actually proved with visuals alone. Unlike that last one you made with the peeling of the circle to find the area which was not proof, only an illustration whish need mathematical proof to support it. This proof needs no maths to support it, we can all see and understand exactly how the areas are equal.
In the strictest sense... NO. To prove that "the area of a regular 12-gon inscribed in a unit-circle is 3" geometrically, one would need to show that the piece fit together with no gaps and no overlaps. Or, we can use some combination of geometry, trig & algebra to show the area to be 3. [Pretty straightforward; everyone should do it for him/herself] This is a great visual "proof" because it touches our intuition in a visually convincing way. Still, it SHOULD spur the curious among us to proving it.
There are visual foolies that deliberately take two things that **LOOK** different, but are actually the same (or the reverse: look the same but are different); for example, there's a famous puzzle where one takes a rectangle, cut it up into some pieces, rearrange and reassemble the pieces so that it APPEARS that there is missing area. [spoiler: there is a long diagonal gap that accounts for the "missing" area... but we discount the gap because (1) the area of the gap because it is "small" relative to the total area; and (2) we implicitly assume that the gap is just imprecision in the cutting or the arranging of the pieces]
What's the great music called?
this is Book of Days. Supposed to be by Enya but this is an alternate version.
Editing software name?
It looks like Manim
It looks like Manim
Area of circle =3x(radius) ^2+ 0.14..... plzz give heart & I found that circumference of circle=Radius/0.1591549......
No, what are you talking about. For a radius of two, that gives an incorrect area of 12.14. It should be 12.566…
@@brandonb6164 bro focus on circumference of circle =radius /1.591549 that is my creation