Can You Pass Cambridge Entrance Exam?
Вставка
- Опубліковано 30 чер 2024
- Entrance examination. If you're reading this ❤️.
What do you think about this problem?
Hello My Friend ! Welcome to my channel. I really appreciate it!
@higher_mathematics
#maths #math
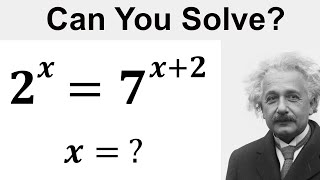








No need for math. The simple mechanical way is to keep dividing by 3 and up the factor by 1 from for each successful division.
As soon as there's a remainder of 1 that's the smallest variable; if the remainder would be 2 we have two variables at once of same value. Subtract 1 from the factor as the remainder was not divided. Keep dividing the dividend ignoring this remainder (as it is already 'factored in') until the dividend is 0.
837/3 -> 279(0)/3 -> 93(0)/3 -> 31(0)/3 -> 10(1): after 4 divisions we have rest 1 which means the original size of the rest=1 * 3³ so z=3.
Continuing with the dividend 10/3 -> 3(1) another rest one factor up; y=4.
Continuing with 3/3 -> 1(0) -> 0(1) two factors up we have another rest of 1, so x =6.
The remaining dividend is zero so we're done.
Heldere uitleg
I think the examinera are looking for the elegant answer: convert 837 to base 3 - 1011000 then by inspection x=6,y=4,z=3. I would score this solution 10/10! Trial and error 2/10 not scholarship material.
At a quick glance I started by calculating powers of 3 and quickly find 3^6= 729 by adding 3^3 = 27 and 3^4 = 81 then 729 + 27 + 81 = 837 . One solution then is x = 3, y = 4 and z = 6.
Thinking in base 3, it's easy to compute that 837 (10) = 1011000 (3), and since base representation of an integer is unique, the only solution to the problem is 3^6 + 3^4 + 3^3.
Any problem of the type "find x,y,z such that N^x + N^y + N^z = M", will have a solution iff the sum of the digits of the base N representation of M is equal to 3.
For the exam: ¿Do you have to write down your deduction or is it sufficient to give the solution and the proof 729 + 81 + 27 = 837?
More faster for my opinion: 3^x is max and
One of the terms must be greater than 1/3 of 837. Only 729 satisfies this, and leaves the sum of the other 2 terms having the last digit as 8. Powers of 3 can only end in digits 3, 7,1 and 9. Therefore perforce the reamaining terms must be 81 and 27.
Got the solution
In Cambridge, UK,it's pronounced zed!
The problem has infinitely many solutions : choose e.g. x= 0 , y=1 .Then z = ln833/ ln 3 . This way you can construct arbitrarly many solutions.
Write down the powers of 3: 1, 3, 9, 27, 81, 243, 729. From that you immediately see that all of the variables must be less than 7 and exactly one of x, y, z must be 6. Thus you reduced the problem to 3^u+3^v=837-729=108. Similarly you can notice that none of u, v can be can be greater than 4 and exactly one of them must be 4. So subtracting again 3^4=81 we reduce the problem to 3^s=108-81=27. Summing it up all the solutions are permutations of 3, 4 and 6.
Ok bat change 837-729 to 108.
@@Cagouille79 Fixed it, thanks!
837 = 9*3*31 =(3^3) (27 + 3 +1) = 3^6 +3^4 +3^0
• digits of 837 add to a multiple of 9 so divide by 9
• 3 divides 93, 31 times
• break down 31 in powers of 3
• done
This takes about 10 seconds by just thinking about the powers of 3.
Maybe more than 10.
There is more better and simply solution
Genial. Gracias-----
Bonne solution .
Radix conversion, usually from base 10 to 2, and 2 to 10, used for all computer calculations, is one of the most common calculations on earth. In this case a radix conversion from 10 to 3 is required.
Conversion of n to radix 3. The process is
1. Find the largest 3^(position - 1) < n.
2. Subtract
3. Repeat until remainder 0.
Giving 3^6 (729) + 3^4 (81) + 3^3 (27) = n (837).
Really good solution. Very quick to compute without much algebra required.
@@emilegiesler9272
Thank you for your compliment : I first wrote a radix conversion program over 50 years ago.
That one was beautiful👏👏
Did it a slightly differently, didnt factor out 3^z. Divided through by 3^3, so indices were x-3, y-3,z-3. Observed that indices must be positive, or wouldnt sum to an integer. ie x,y,z>=3. However, if they were all stricly greater than three, you could take a factor of 3 from the whole expression and divide through, which you cant because 31 is prime. Therefore one index must be precisely 0. say x-3=0, x=3. sub in, and subtract 1 from each side and you have the remaining terms sum to 30. But 30 has a factor of 3, so you can divide through to have the indices as y-4,z-4 and equalling 10. Trivially 9 and 1, which yield 5 and 13 respectively.
How is it concluded that 3^z = 3^3?
No Power of 3 is equal to 31
Excellent exercise for understanding some the equations with multiple variables. I would not think on the multiple combinations of solutions, this is what I learned today. Thank you
Such sigma math, so skibidi sus ohio vibes like that 10/10 fanum tax gyat