How Ramanujan proved his master theorem

• A RIDICULOUSLY AWESOME...
• Ramanujan's master the...
15 percent off everything using the code MATHS505 on Advanced MathWear:
my-store-ef6c0...
Complex analysis lectures:
• Complex Analysis Lectures
If you like the videos and would like to support the channel:
/ maths505
You can follow me on Instagram for write ups that come in handy for my videos:
...
My LinkedIn:
/ kamaal-mirza-86b380252

[@Calcprof]

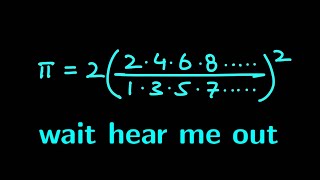
The normal proof (whatever that is) that I know is based on the operational form of Taylor's theorem: f(x+ε) = e^(ε(d/dx)) f. A gap in your proof is that you have to show, since, in the proof, g is given first, that given any φ satisfying the hypotheses, we can solve for an analytic g satisfying g(a + hr^s) = φ(s)

[@maths_505]

Not a big fan of that either. Hardy's proof using residues is brilliant beyond measure.

[@mcalkis5771]

Ramanujan seriously needs some more love. Hope yo see you cover more of his amazing work.

[@ahmetalicetin5331]

Thanks. I have been tackling with this for a while and it is nice to see a video about it from a high quality channel like you.

[@MrWael1970]

Thanks for your effort

[@123bluestorm1]

Hey, I've been following your videos for a long time now. I spent last summer watching your videos, and it has been a blast getting better at solving integrals. I do wonder if you have any recommendations for books that I can use to get familiar with the techniques you use? It would be a great pleasure, thank you so much.

[@maths_505]

I'll mention some in a Q/A video I plan on doing later this month

[@aravindakannank.s.]

we want g.h.hardys proof as soon as possible ❤

[@ashishraje5712]

Very nice

[@illumexhisoka6181]

Why is it that important when it have this many conditions ?

[@maths_505]

The conditions aren't all that bad tho.

[@Risu0chan]

I suppose we need them so that we can safely swap the integral and summmation signs (with the dominated convergence theorem, perhaps? I'm not sure)

[@csilval18]

Not a big fan of just interchanging series and integrals, at least comment on why it's possible (Fubini, dominated convergence, and why the conditions are met)

[@victormarchant217]

I can't wait to see Hardy's proof

[@RagaGian]

What kind of transformation?

[@maths_505]

Mellin transform

[@RagaGian]

@@maths_505 Thanks. That's great

[@juandiegoparales9379]

I have to see the proof by hardy!

[@adhamcomstock4409]

Balsagna chin

[@Noam_.Menashe]

I'm sorry but your r's look a lot like gammas.

[@nightmareintegral5593]

Wanna better minature?
I sended you.

[@maths_505]

Where?

[@nightmareintegral5593]

@@maths_505 i sended png on gmail

[@nightmareintegral5593]

@@maths_505 I sended png on gmail

[@ELBARTO2023-bg1rw]

😂

[@petterituovinem8412]

first

[@nullvoid12]

Can someone provide a context?

[@maths_505]

Context for what mate?

[@nullvoid12]

@@maths_505 what is this theorem about?

[@maths_505]

@@nullvoid12 it's primarily used to derived melin transforms of functions.