Modular Arithmetic: Pick the Right Number | Putnam 2001 A5
Вставка
- Опубліковано 30 вер 2024
- #Math #Putnam #NumberTheory
In this video we solve a problem from Putnam 2001.
Subscribe @letsthinkcritically !!
------------------------------------------------
I share Maths problems and Maths topics from well-known contests, exams and also from viewers around the world. Apart from sharing solutions to these problems, I also share my intuitions and first thoughts when I tried to solve these problems.
Subscribe: www.youtube.co...
Email me (address in video) your suggestions! lets.think.critically.27@gmail.com


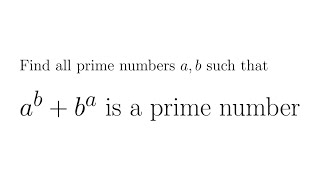






I like this kind of problems, because it is really funny when you take the mod of the variable you need to find!
ua-cam.com/video/HMHLL4YAXdc/v-deo.html
There's another pair of consecutive divisors of 2002: they're 1 and 2
yes, but 1^n-2^(n+1)=2001 has no integer solution
ua-cam.com/video/HMHLL4YAXdc/v-deo.html
Probably the most purest NT problem in Putnam ever , loved it !
ua-cam.com/video/HMHLL4YAXdc/v-deo.html
I solved it without modular arithmetic.
set n=1, no solutions (just do quadratic formula)
set n=2, you get a cubic polynomial, solve with RRT (you can disregard non-rational solutions of course)
so you find (13, 2) is a solution
and obviously a can't be bigger than 13
so you can test all possible a values between 1...12. Brute force it to show there are no solutions and you're done
actually, you'd only have to check for a up to 8, since 8^4-9^3=3367
ua-cam.com/video/HMHLL4YAXdc/v-deo.html
Excuse me why can't a be bigger than 13
.you don't k own that it could.be any positive integer o ly restriction is a^n times a has to be bigger than the subtracted part of (a +1)^n to get a positive number.did you plug I. 14 or somethingto guessand check??.
wouldnt it be faster to show that there are no solutions for n>2 by calculus?
ua-cam.com/video/HMHLL4YAXdc/v-deo.html
That’s what I thought. LHS is monotonically increasing. Rhs is constant. There can only be one solution.
@@chriswinchell1570 Well, actually LHS is not monotonically increasing. It has a maximum at n=18 and then decreases to -inf.
Good one. I got part way into this by expanding the binomial and adding 1 to both sides. The LHS then has "a" as a factor and the right hand side is 2002 so I quickly knew a|2002.
Playing around with mod 3 shows n is even.
But that's as far as I got!!!!!!!
ua-cam.com/video/HMHLL4YAXdc/v-deo.html
I also did exactly this, and I also found that a = 1 (mod 3) - i.e. that a must be one of the 8 divisors of 2002 which are congruent to 1 modulo 3. (1, 7, 13, 22, 91, 154, 286, and 2002)
I then just did the casework for these, which actually turned out to be very simple!
a = 1, a = 7 give no solutions.
a = 13 gives the (only) solution, (13, 2).
A simple calculus argument (assuming n is real) shows that the larger a is, the smaller n is for equality to hold. But since n is natural it must be exactly 1, as that is the only natural number less than 2, but this yields no solutions for a = {22, 91, 153, 286, 2002}. By the way, if we take 0 as a natural, we also get (2002,0). :)
I'm actually surprised that this is on the Putnam at all, since it's just destroyed by high school calculus and simple logic and casework, lol.
Also a=2002 and n=0
ua-cam.com/video/HMHLL4YAXdc/v-deo.html
that was also my first (good) guess. But nobody talks about it...
@@waitinblackout due to the fact that they have the set of whole numbers, which are positive integers with zero: 0,1,2 etc.
That's why (probably) he didn't take 0
The problem implies naturals, not wholes
Surely the mod 8 trick at the end is not necessary. You can just prove that 13^(n+1) - 14^n is a strictly increasing function when n > 2, so it never returns to the value 2001.
(13^(n+2) - 14^(n+1)) - (13^(n+1) - 14^n) = (13^(n+1) - 14^n)*13 + 14^n
This is guaranteed to be positive if 13^(n+1) - 14^n > 0, which we know holds true for n=1, so by induction it's true for all n. Right?
I thought so, but it's not right. 14^n is asymptotically bigger than 13^(n+1), so for big enough n, 13^(n+1)
When I solved it I was like ok but then I realised it was Putnam problem holy shit lol
ua-cam.com/video/HMHLL4YAXdc/v-deo.html
My solution before watching the vid:
(a)^(n+1) - (a+1) ^(n) + 1 = 2002
Since (a) is factor of left hand side of eqn (using binomial) therefore "(a) is a factor of 200"__1st eqn.
Now, given eqn can be written as:
(K-1) ^(n+1) - k^(n) + 1 = 2002 [ where k=a+1]
Again we have k as factor of LHS, so "k=(a+1) is factor of 2002__2nd eqn"
Now using our 1st and 2nd eqn we can say a(a+1) ia a factor of 2002.
We can write 2002 = 1*2*7*11*13
Or 2002 = 13*14*11
So a = 1 or a =13.
Clearly a= 1 gives no solution(couz LSH become -ve)
So a = 13
Finally, putting a = 13 in the eqn can making some logical guess for n,
We get 13^3 - 14^2 = 2001,
Therefor a=13 and n=2.
ua-cam.com/video/HMHLL4YAXdc/v-deo.html
Hi can u tell me how approxh to solve putnam problam
that was problem A5? lolz
ua-cam.com/video/HMHLL4YAXdc/v-deo.html
This is a good problem, combining a few ideas. I got as far as the 13,14 bit but didn't think of mod 8.
Why would anyone thinknof mod 8..just use mod 2 since 2002 is zero mod 2
It is intuitive actually since 3² - 1 = 8
Nice✌🏻
ua-cam.com/video/HMHLL4YAXdc/v-deo.html
I can't remember: Is calculus allowed on the Putnam? If it is, you might consider the following for the proof that n = 3 is the only valid value of n:
Let f(x) = a^(x+1) - a^x, with a = 13 in this case.
Then f'(x) = lna((x+1)a^(x+1) -xa^x) > f(x) > 0 for all x≥1. Similarly, f''(x) > 0 for all x≥1.
Therefore f is increasing at all natural x, so f(x) = 2001 can only be true at x = 3.
Admittedly, I might have skipped a couple of steps in the middle, but how's that?
great job, thanks for sharing
ua-cam.com/video/HMHLL4YAXdc/v-deo.html
Finally a competition problem!
ua-cam.com/video/HMHLL4YAXdc/v-deo.html
Why did you use from zero measure for a?
Because a is natural number, right?!
ua-cam.com/video/HMHLL4YAXdc/v-deo.html
👍👍👍
ua-cam.com/video/HMHLL4YAXdc/v-deo.html