
- 212
- 59 096
dR. bAbAk
Sweden
Приєднався 17 лют 2009
I publish mathematics and physics educational videos on this channel from the advanced high school level to the university level.
I have taught mathematics and physics for over 30 years, from high school to university. I have held a Ph.D. in mathematical physics from Stockholm University since 2017. I am the head of the Mathematics Department of the Arena Academy, a Swedish high school in Stockholm. I also partly teach at the Mathematics Department of KTH, Royal Institute of Technology, Stockholm, Sweden, and the Physics Department of Stockholm University.
The following is another UA-cam channel on which I upload my lectures at Arena Academy.
ua-cam.com/users/MathematicsatINITCollege
I have taught mathematics and physics for over 30 years, from high school to university. I have held a Ph.D. in mathematical physics from Stockholm University since 2017. I am the head of the Mathematics Department of the Arena Academy, a Swedish high school in Stockholm. I also partly teach at the Mathematics Department of KTH, Royal Institute of Technology, Stockholm, Sweden, and the Physics Department of Stockholm University.
The following is another UA-cam channel on which I upload my lectures at Arena Academy.
ua-cam.com/users/MathematicsatINITCollege
Problems and Solutions, Group Theory, Basics, Problem 4
In this video, I walk you through a practical and approachable problem in introductory group theory.
#maths #abstractalgebra
#maths #abstractalgebra
Переглядів: 51
Відео
2D-Motion, Problem 1
Переглядів 17916 годин тому
A nice problem in 2D-Motion. #calculus #mechanics #classicalmechanics #projectiles #physics
Problem 5.4, Classical Mechanics, R. Douglas Gregory
Переглядів 25514 днів тому
In this video, I discuss the solution to problem 5.4 in the book "Classical Mechanics, R. Douglas Gregory, Cambridge University Press, 2006".
Problem 5.3, Classical Mechanics, R. Douglas Gregory
Переглядів 33014 днів тому
In this video, I discuss the solution to problem 5.3 in the book "Classical Mechanics, R. Douglas Gregory, Cambridge University Press, 2006".
Harmonic Oscillator, Problem 1 #shorts
Переглядів 26614 днів тому
#shorts #physics #mechanics #kinematics #maths
Problem 40, Section 6.5, Page 370 (Calculus, A Complete Course, 10th Edition, Adams & Essex)
Переглядів 32821 день тому
🔍 Stuck on a Problem in This Book? Let Me Help! 🔍 Struggling with a tough problem in this textbook? Don't fret! 🤔💡 Drop a comment below this video, and I'll do my best to make a dedicated video for you! 📚✏️ 🚀💬 Don't forget to like and subscribe! 🌟🔔 In this video, I solve problem 40, Section 6.5, Page 370 in the book "Calculus, A Complete Course, 10th Edition, Robert J. Adams and Christopher Ess...
Problem 39, Section 6.5, Page 370 (Calculus, A Complete Course, 10th Edition, Adams & Essex)
Переглядів 26321 день тому
🔍 Stuck on a Problem in This Book? Let Me Help! 🔍 Struggling with a tough problem in this textbook? Don't fret! 🤔💡 Drop a comment below this video, and I'll do my best to make a dedicated video for you! 📚✏️ 🚀💬 Don't forget to like and subscribe! 🌟🔔 In this video, I solve problem 39, Section 6.5, Page 370 in the book "Calculus, A Complete Course, 10th Edition, Robert J. Adams and Christopher Ess...
Problem 38, Section 6.5, Page 370 (Calculus, A Complete Course, 10th Edition, Adams & Essex)
Переглядів 23421 день тому
🔍 Stuck on a Problem in This Book? Let Me Help! 🔍 Struggling with a tough problem in this textbook? Don't fret! 🤔💡 Drop a comment below this video, and I'll do my best to make a dedicated video for you! 📚✏️ 🚀💬 Don't forget to like and subscribe! 🌟🔔 In this video, I solve problem 38, Section 6.5, Page 370 in the book "Calculus, A Complete Course, 10th Edition, Robert J. Adams and Christopher Ess...
Problem 4.31, Classical Mechanics, R. Douglas Gregory
Переглядів 15621 день тому
Problem 4.31, Classical Mechanics, R. Douglas Gregory
Problem 37, Section 6.5, Page 370 (Calculus, A Complete Course, 10th Edition, Adams & Essex)
Переглядів 41321 день тому
Problem 37, Section 6.5, Page 370 (Calculus, A Complete Course, 10th Edition, Adams & Essex)
Problems and Solutions, Group Theory, Basics, Problem 3
Переглядів 12121 день тому
Problems and Solutions, Group Theory, Basics, Problem 3
Problems and Solutions, Group Theory, Basics, Problem 2
Переглядів 50421 день тому
Problems and Solutions, Group Theory, Basics, Problem 2
Group Theory, Basics, Problem 2, #shorts
Переглядів 26121 день тому
Group Theory, Basics, Problem 2, #shorts
Introductory Kinematics, Problem 1 #shorts
Переглядів 25528 днів тому
Introductory Kinematics, Problem 1 #shorts
Group Theory, Basics, Problem 1, #shorts
Переглядів 24028 днів тому
Group Theory, Basics, Problem 1, #shorts
Problems and Solutions, Group Theory, Basics, Problem 1
Переглядів 1,2 тис.Місяць тому
Problems and Solutions, Group Theory, Basics, Problem 1
Problem 4.18, Classical Mechanics, R. Douglas Gregory
Переглядів 696Місяць тому
Problem 4.18, Classical Mechanics, R. Douglas Gregory
Mathematical Logic, Predicates and Quantifiers, Part 2
Переглядів 9874 місяці тому
Mathematical Logic, Predicates and Quantifiers, Part 2
Mathematical Logic, Predicates and Quantifiers, Part 1
Переглядів 3304 місяці тому
Mathematical Logic, Predicates and Quantifiers, Part 1
Mathematical Logic, Propositions Algebra
Переглядів 1034 місяці тому
Mathematical Logic, Propositions Algebra
Mathematical Logic, Logical Equivalence
Переглядів 8814 місяці тому
Mathematical Logic, Logical Equivalence
Mathematical Logic, Propositions and Logical Connectives, Part 2
Переглядів 5635 місяців тому
Mathematical Logic, Propositions and Logical Connectives, Part 2
Mathematical Logic, Propositions and Logical Connectives, Part 1
Переглядів 3065 місяців тому
Mathematical Logic, Propositions and Logical Connectives, Part 1
Problems and Solutions, Definite Integrals, Problem 4
Переглядів 5709 місяців тому
Problems and Solutions, Definite Integrals, Problem 4
Problems and Solutions, Definite Integrals, Problem 3
Переглядів 6509 місяців тому
Problems and Solutions, Definite Integrals, Problem 3


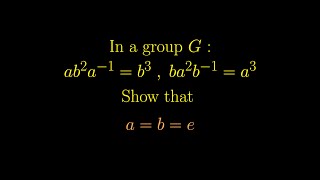






Great .. Thank you very much
@@najibhh8912 You are welcome 🙏
Great .. Thank you
Welcome 😊
Very nice. Can you explain what motivated your initial decision to play around with b⁹, and how it was you had the confidence to keep going when it looked halfway through as though the expressions were just getting more complicated rather than less?
Thank you for your thoughtful question! What you see in the video is the final, polished version of the solution, but getting there involved a lot of trial and error-scribbling on scratch paper, failing, reworking, and refining. This process is very common in mathematics, as the final solution often hides the messy, behind-the-scenes efforts. When working on abstract algebra problems, especially during my undergraduate studies in pure mathematics, I learned that intuition is often limited, and solving such problems requires persistence and experience. The decisions to explore specific paths, like working with b^6 and b^9, were motivated by the relationships between the given powers (b^2 and b^3) and how they naturally connect to higher powers like 6 and 9. That said, even in retrospect, I sometimes feel I might have overcomplicated the problem. That’s why I invite viewers to share their insights-it’s always possible there’s a simpler solution I overlooked. Collaboration and different perspectives are invaluable in mathematics.
@@dR-bAbAk Thanks for your reply. I suppose what puzzles me most of all is that, in any situation where I might be trying random things out for a problem like this, regrouping products in different ways to try to make use of the given identities to find some simplification or cancellation, if I ever found myself writing down fourth or sixth powers of an element - let alone the ninth! - (given that in the statement of the problem the highest power was the third), I would automatically assume that the track I was on was very much the wrong one, and I cannot conceive that I would have the obstinacy or self-belief to persist. I also wonder how results like this get discovered in the first place: after all, if one finds such a problem in a textbook, one is generally safe to assume that it is actually true, and I can see that that might give one the confidence required to carry on. But what would motivate someone to pursue such arcane avenues if one didn't already have this assurance? Having said all that, and reviewing your solution and your remarks on the relationship between 2, 3, 6, and 9, I think I can now at least conceive of a hint that might possibly have put me on the right track. Namely to focus on the fact that (writing * for inverse here, for legibility) (ab²a*)³ = (ab³a*)².
@russellsharpe288 I see your point. I have never seriously delved into designing novel problems. Personally, I prefer working on a given problem rather than creating a beautiful one-I don’t think I’m particularly talented in that regard.
🎉
Thank you!
Thank you very much 👍
You are welcome 🙏
I loved this. I stopped the video and tried to prove it myself. After struggling for a while, I persevered and struggled a while longer, eventually proving it myself. Then I watched the video, and found that you had done it a different way. So I get a bonus extra lesson: there is more than one way to do it!
Great! I am happy for you.
Thank you very much 👍👍
You are welcome
Great job .. Thank you
Thank you too!
Thank you very much for all your videos which helped me a lot to understand different mathematical topics.. Really appreciated..
You are most welcome
As usual.. fantastic.. Thank you
Thank you so much.
This is overly complicated, you can get the same result in like 2 lines
@@TC159 can you please elaborate on how?
@dR-bAbAk sure, do you have an email, so I can send compiled LaTeX to once I'm home?
@@dR-bAbAk I don't think my other comment went through. So please excuse me if the message isn't really clear on what I mean. a*b = a+b-ab can be factored as 1-(a-1)(b-1) this gives a clue on how to prove your result. What I'll do next is essentially provide an isomorphism (of semigroups) but due to its simple nature it could be redone without it being done explicit. Take phi: x -> 1-x (a mapping from R to R). This map is clearly bijective. Notice now that phi(a*b) = phi(a+b-ab) = 1-a-b+ab = (1-a)(1-b) = phi(a)phi(b). Hence phi is a semigroup isomorphism, with the image space having the regular real number multiplication. In particular, we know R to be a group if we remove 0.
@@TC159 Thank you for your instructive comment. I truly enjoyed your elegant idea of using isomorphism to solve the problem, and I appreciate you sharing it with me. To explain my approach, I would like to outline three points: 1. Although I did not explicitly mention it in the video, I was implicitly assuming that I was using only the theorems, definitions, and concepts covered in the first chapter of any standard undergraduate Abstract Algebra textbook. Therefore, I did not expect the audience to be familiar with the notion of group isomorphism at this stage. 2. If you were to explain your idea in a video to make it clear to your audience, I believe it would still require approximately the same amount of time as my video, considering time as a good measure of complexity. You would need to verify the associativity of the binary operation, explain the construction of the isomorphism, and prove that it is indeed an isomorphism. I fully agree that for an experienced person, once your idea comes to mind, the rest can follow almost instantly. This is why I acknowledge that your approach is more powerful than the one I presented. However, from a teaching perspective, I often advocate for solutions that involve following standard steps. This approach ensures that learners can solve many problems, even if their solutions are not the most innovative or elegant. From my experience of many years in mathematics, I understand that the most exciting moments come not when we find standard solutions but when we discover elegant and extraordinary approaches. The ability to do the former relates to the effort we put into our learning, while the latter often depends on innate talent. This seemingly paradoxical contrast between what we enjoy the most and what we can actually achieve is perhaps one of the greatest driving forces in life, and mathematics is no exception. Unfortunately, current scientific research supports the idea that we have limited control over the latter. This brings me to my final point. 3. I simply could not see your solution 😊 My apologies for becoming too philosophical. Thank you again for your thoughtful comment and for contributing to this discussion.
Hello, thanks for the video. This could just be a personal issue but I found the board a little difficult to read since the text is small. My only constructive criticism would be to make text relatively larger. Nonetheless, great video!
Thanks for the instructive comment. I agree with you. I will try write larger.
marvelous video
Thank you. I am glad that you found it useful.
I learn a lot from your videos and this video like other videos you published,Very informative and very helpful for all people who likes to learn Abstract Algebra.. Thank you very much
I am delighted that you find my videos helpful. Thanks for the encouraging comment!
@@@@
Helo 👍🌽🖐
Hello! 🙂
Thank you Babak for the amazing video :)
You are welcome. I am happy that you liked it. By the way, I didn't know that you are also following my videos on this channel as well.
Thank you, the video helped me a lot!!! God bless you!
I am happy you found it helpful. God bless you too!
Excellent explanation 👍
Thanks 🙏
29:39 I missed a factor of 3 in the denominator. This will slightly affect the details of the upcoming calculations but won't change the overall approach or the key results.
thanks a lot. wish every instructor one day to be as you.
You are welcome. Thanks for your kind comment.
Are there will be first order theory, interpretations etc.?
Hopefully, it will come.
anna thank u anna suuper anna u i lobe u anna plsz anna okka footo anna pleees anna
keep going ♡
Thanks for the encouragement. I will!
Hi sir how are you doing? I am your subscriber ❤
Hi, I am doing well. I hope the same for you. My pleasure!
Your viewers by enjoyed this video of a model. 0:15 ua-cam.com/video/wrBsqiE0vG4/v-deo.htmlsi=3RF3qV49JIG_gtNN
As somebody about to go into calc 2 in second semester, those partial fractions give me a vague sense of terror (along with polar coordinates)
Don't worry! You just need to practice. It is not as hard as it looks. Good luck with your studies.
At 12:58, I mean superficial :)
Just finished watching your videos on Abstraction in mathematics. Those videos were great. Thank you for sharing on UA-cam. Do you have any plans to make video on how to read and understand mathematics ? Or do you know any books which can teach me that.
I'm thrilled to hear that you find the videos helpful, and I truly appreciate your encouraging comment. While my channel may not have garnered a large audience yet, your support keeps me motivated. It is challenging to stay enthusiastic throughout projects, especially when faced with a smaller audience. As for creating videos on how to read and understand mathematics, it's not in my current plans. However, I can recommend some excellent books that might help you in that regard: 1. A Logical Introduction to Proof, by Daniel W. Cunningham (www.amazon.com/Logical-Introduction-Proof-Daniel-Cunningham/dp/1461436303/ref=tmm_hrd_swatch_0?_encoding=UTF8&qid=1703261511&sr=1-1) 2. Mathematical Writing, by Franco Vivaldi (www.amazon.com/Mathematical-Writing-Springer-Undergraduate-Mathematics/dp/1447165268/ref=sr_1_1?crid=2M2NO9TKQFT32&keywords=mathematical+writing&qid=1703261451&s=books&sprefix=mathematical+writin%2Cstripbooks-intl-ship%2C297&sr=1-1) 3. Transition to Advanced Mathematics, by Danilo R. Diedrichs, and Stephen Lovett (www.amazon.com/Transition-Advanced-Mathematics-Textbooks-ebook/dp/B09YVTHXZH/ref=sr_1_8?crid=1JF881LHOLNLL&keywords=transition+to+advanced+mathematics&qid=1703261005&s=books&sprefix=transitio%2Cstripbooks-intl-ship%2C328&sr=1-8) I hope you find the books helpful. Good Luck!
@@dR-bAbAk Thank you for your feedback. Your videos are really great with positive aura. Wish you all the best. God bless you.
Imagine spending your life on this waste that has helped no one, ever
That you are using UA-cam platform is in its own an indication that this has already helped you 🙂. Without these mathematical concepts, these level of technology would be impossible!
free balstaen
I adore your videos
Thank you. I am happy that you like them.
Very good
Thanks!
Thank you I got so stuck 😅
Welcome
"PromoSM" 👌
At 15:32, I should have written "=" rather than "<=".
We are very interested . Please produce more videos. We will try to popularize these lectures as far as possible by us. Thank you so much.
I am glad you like it. I would appreciate it if you could popularize my videos. This definitely encourages me to work more enthusiastically.
Another good example of abstraction is numbers, we use them to discuss and quantify our possessions. If I were to say “seven cars” you can start to imagine seven cars in your head. Essentially abstraction is a way, or rather the process of when you drop and forget physical as well as concrete details that do not relate to the phenomenon we are trying to comprehend.
Yes, true. I ran out of time and could not cover that. Now I intend to have one more session on "Abstraction" before switching to the next topic of Mathematical Logic.
Thanks please update more videos on QM
You are welcome. Right now, I am busy with other projects, but I will do my best to do so.
Is that right?
Yes, it is. Don’t you think so?
The correct exponent of the denominator in the final answer should be a five. I mistakenly wrote six.
I am sorry for the video being a little bit shaky. I hope that it is not too much disturbing.
??????
Is that so puzzling? 🙂
@@dR-bAbAk ...no señor...escribí algo que no se transmitió...tarde me di cuenta del error...gracias igual Señor
This is good, I expected him to use the sec into tan trig sub, but this seems more streamlined and intuitive as well. 🤙
As it's multiple choice - even with a rough sketch it's easy to see that the area is definitely more than 2, which eliminates all answers but one, No calculus needed.
You are right. I should have been more careful about the choices of the options 😊
@@dR-bAbAk For a non multiple choice question, maybe extend the range to -1 to 1 instead of 0 to 1, and the insightful can reduce the calculus needed (by symmetries) and reduce the risk of tripping up on a lost - sign.
@@michaeltempsch5282 Of course, for a non multiple choice question, getting the exact answer 17/6 without using calculus, or any other exhaustion method is not possible. So, I don’t think in that case, I need to change anything for a “shorts” video. Actually, 17/6 represents the area of the given region by how we define the notion of the area in calculus. Area is defined by a definite integral.
@@dR-bAbAk Absolutely, you can't eliminate calculus completely, but seeing that you don't need to involve the y= -x part at all, and that the rest is equal to 2x the integral of x²+2 from 0 to 1 does simplify things... (IMHO at least). And I wasn't thinking in terms of shorts.
@@michaeltempsch5282 Thanks for your constructive comments.
Nice
Lol
At 3:11, I mistakenly kept the factor of 1/3 on the left side. That is not correct. Of course, I calculated the integral correctly.
Robert California teaches math?
Do you think I look like him? 🙂
I used a different substitution for my answer, letting 1-x^3 in the integral be equal to t. It simplified the first limits and made the rest really easy since you basically got the same integral twice as a result.
Thanks for the comment. Do you mean when computing I(y)? If so, I chose that substitution because I prefer to have no surds in my integrand after the substitution. If I understood you right, after your substitution, the integral, up to a factor, becomes $\int_{1}^{y^3}\sqrt{t-y^3} dx$. I agree that the limits are simpler, but the integrand contains a square root. Technically speaking, one must introduce another substitution to solve the new integral. Of course, since $y^3$ is a constant, the primitive function will be 2/3(t-y^3)^(3/2). To appreciate the substitution that I used in the video, try to solve the integral $\int_{0}^{1}x^2\sqrt[5]{1+x} dx$. To compute this, I hope that you agree that introducing 1+x to be t^5 rather than t makes life after substitution easier from an integration point of view. Still, the price I should pay is to work with limits 1 and $\sqrt[5]{2}$ rather than with simpler limits 1 and 2, as in the case of the latter substitution.