
- 8
- 30 106
Shubham V Deshmukh
India
Приєднався 25 тра 2017
Conditional Formatting in MS Excel: Highlight Matched Data in list A comparing list B
Highlight Matched Data In MS Excel: Conditional Formatting
Highlight the matched data in list A comparing list B.
Highlight the matched data in list A comparing list B.
Переглядів: 276
Відео
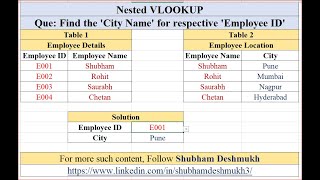
Nested VLOOKUP
Переглядів 1673 місяці тому
🚀 Master Nested VLOOKUP in Excel! 🚀 🔍 Tired of sifting through data? Nested VLOOKUP can be your ultimate time-saver! Check out my latest video where I break down the steps to efficiently use this powerful Excel function. 📊 Whether you're a beginner or looking to enhance your Excel skills, this tutorial is for you. Learn how to streamline your data lookup process and become an Excel pro! 🎥 Watch...
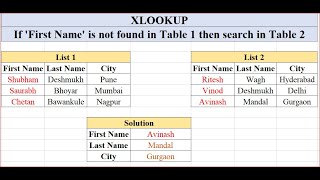
Nested XLOOKUP in MS Excel
Переглядів 383 місяці тому
Nested XLOOKUP in MS Excel: If 'First Name' is not found in Table 1 then search in Table 2
Finite Difference Method.
Переглядів 3604 роки тому
Finite Difference Method is one of the Numerical Method which gives most accurate results as compared to other Numerical Methods. Online Equation Solver Link: www.math.odu.edu/~bogacki/cgi-bin/lat.cgi?c=sys Subdomain Method:ua-cam.com/video/qHBf7uSZmts/v-deo.html Collocation Method: ua-cam.com/video/u8dVrzxTvSA/v-deo.html Petrov Galerkin Method: ua-cam.com/video/qHBf7uSZmts/v-deo.html Finite Di...
Petrov Galerkin Method - Weighted Residue Method.
Переглядів 3,5 тис.4 роки тому
Petrov Galerkin Method is one of the Numerical Method to solve Differential Equation approximately. Subdomain Method:ua-cam.com/video/qHBf7uSZmts/v-deo.html Collocation Method: ua-cam.com/video/u8dVrzxTvSA/v-deo.html Petrov Galerkin Method: ua-cam.com/video/qHBf7uSZmts/v-deo.html Finite Difference Method: ua-cam.com/video/cB8_riC18CA/v-deo.html
Subdomain Method - Weighted Residue Method.
Переглядів 1,5 тис.4 роки тому
Subdomain Method is one of the Numerical Method to solve Differential Equation approximately. Subdomain Method:ua-cam.com/video/qHBf7uSZmts/v-deo.html Collocation Method: ua-cam.com/video/u8dVrzxTvSA/v-deo.html Petrov Galerkin Method: ua-cam.com/video/qHBf7uSZmts/v-deo.html Finite Difference Method: ua-cam.com/video/cB8_riC18CA/v-deo.html
Collocation Method - Weighted Residue Method.
Переглядів 21 тис.4 роки тому
Collocation Method is one of the Numerical Method to solve Differential equation approximately.
#ThresherMachine. | Human Powered Groundnut Thresher Machine. | Pedal Operated Thresher.
Переглядів 3,3 тис.5 років тому
●Project Title:- "Design and Development of Human Powered Groundnut Thresher Machine." ●Introduction:- This “Human Powered Groundnut Thresher Machine” separates the groundnuts from the roots of the groundnut plant. The main objective of this manually operated model is that it can be affordable by any small scale farmers in terms of cost and can be used in power shortage area. The small scale fa...






The way you explain is so good, thanks so much
Glad it was helpful!
Hi bro please provide all your notesof finite element analysis please
whta bibliografy do you used?
Your name is shoom dishoom ? 😅
Make a video for last squer method weighted residuals. Please
please provide me a reference book
Nice video to grab the method...
Great teaching style
Sir, can we choose any point as gauss point?
Here, the limit is 0 to 1. We need two gauss points. So, we need to divide 0 to 1 into three equal parts to get two gauss points (shown at 9.07 minutes in the video). So, points (1/3) & (2/3) divide limit into three equal parts and hence two gauss points are obtained.
Sir can you explain how you found that gauss points,??? 1/3 and 2/3?
Here, the limit is 0 to 1. We need two gauss points. So, we need to divide 0 to 1 into three equal parts to get two gauss points (shown at 9.07 minutes in the video). So, points (1/3) & (2/3) divide limit into three equal parts and hence two gauss points are obtained.
@@shubhamvdeshmukh7625 Ohk....Thank You So Much Sir🙏😊
How did we understand that we need 2 gauss points?
This is so good. After breaking my head on reading theory, this simple explanation made more sense. Thank you so Shubham :)
Hey, can you make a video with FEM in the same way of this video ? Your explanation was nice
Thank you!
Very nice, simple, and lucid lecture about the point collocation method. I became interested in finding out how the method of collocation works because I recently learned to use the solve_bvp function of SciPy for Python and it uses collocation to solve the BVP. The collocation method isn't usually mentioned in numerical methods books. The shooting and finite difference methods are the ones usually mentioned. The collocation method is mentioned in only one of the books I have and only in passing without detailing how it works and no examples.
Good Luck!
How find the exact soulution
The ode for this problem is a 2nd-order, linear, non-homogenous ODE with constant coefficients. For a non-homogenous ODE, you can use the method of undetermined coefficients (MUC) or method of variational parameters (MVP). Since the we have constant coefficients for this one, MUC is applicable. The forcing function here is just a constant, -1, so your steady state solution is of the form yss = k. k = -1 for this problem. The total solution is composed of the homogenous solution and the non-homogenous solution (y = -1). For the homogenous solution, you just equate the sum of y and its derivatives to zero and substitute y=e^(at) in the ODE and solve for a.
Thank you, very short and simple explanation
Thank you sir
How we are choosing Gauss points here?
same doubt i had as well
You can choose any point for the collocation. What matters is that those collocation points satisfy the governing differential equation, which you do by substituting those points into the ODE.
Here, the limit is 0 to 1. We need two gauss points. So, we need to divide 0 to 1 into three equal parts to get two gauss points (shown at 9.07 minutes in the video). So, points (1/3) & (2/3) divide limit into three equal parts and hence two gauss points are obtained.
Commendable job dear sir
Thank You Sir!
Good job
Tnank You.
Contact number
Good info
Thank You so much.
Awesome bro. God bless you
Thank You so much 😊😊
Nice bro
Thanks Aman Bhai!
Awesome bhai👍
Thanks Vikrant!