
- 408
- 151 914
math&physics with intuition
Приєднався 27 тра 2011
Here I share my videos/lectures on scientific subjects such as mathematics, modern physics (Relativity, Quantum Mechanics, etc), but also engineering.
why is quantum gravity so hard?
Why is quantum gravity so challenging?
Quantum gravity seeks to unify quantum mechanics and general relativity, but it faces profound difficulties due to its mathematical structure.
At its core lies the Einstein-Hilbert action, which describes gravity as a geometric theory. Using natural units, the strength of gravitational interactions is tied to the Planck mass, an extremely large energy scale.
Small perturbations around flat spacetime reveal that the theory involves an infinite series of interaction terms. These terms grow increasingly significant at higher energies, making the theory harder to interpret.
The main obstacle is that gravity, in its quantum form, is a non-renormalizable theory. This means that the infinite divergences it produces cannot be consistently managed with a finite number of adjustments, posing a fundamental challenge to developing a complete and predictive framework for quantum gravity.
This post was inspired by professor David Tong’s notes.
#QuantumGravity #GeneralRelativity #TheoreticalPhysics #Einstein #Science #Physics #Math #quantumfieldtheory #mathematics #mathematician #lovemath #mathlover #physicslover #quantumphysics #CurvedSpacetime #QuantumFieldTheory #TheoreticalPhysics #MathematicalPhysics #Quantum #PhysicsCommunity #Patreon
Quantum gravity seeks to unify quantum mechanics and general relativity, but it faces profound difficulties due to its mathematical structure.
At its core lies the Einstein-Hilbert action, which describes gravity as a geometric theory. Using natural units, the strength of gravitational interactions is tied to the Planck mass, an extremely large energy scale.
Small perturbations around flat spacetime reveal that the theory involves an infinite series of interaction terms. These terms grow increasingly significant at higher energies, making the theory harder to interpret.
The main obstacle is that gravity, in its quantum form, is a non-renormalizable theory. This means that the infinite divergences it produces cannot be consistently managed with a finite number of adjustments, posing a fundamental challenge to developing a complete and predictive framework for quantum gravity.
This post was inspired by professor David Tong’s notes.
#QuantumGravity #GeneralRelativity #TheoreticalPhysics #Einstein #Science #Physics #Math #quantumfieldtheory #mathematics #mathematician #lovemath #mathlover #physicslover #quantumphysics #CurvedSpacetime #QuantumFieldTheory #TheoreticalPhysics #MathematicalPhysics #Quantum #PhysicsCommunity #Patreon
Переглядів: 8
Відео
Semiclassical gravity
Переглядів 454 години тому
Semiclassical gravity is an approximation to the theory of quantum gravity in which one treats matter and energy fields as being quantum and the gravitational field as being classical. In semiclassical gravity, matter is represented by quantum matter fields that propagate according to the theory of quantum fields in curved spacetime. For a detailed walkthrough of the derivations, visit either t...
Derivation of the Unruh effect: Scalar field in curved space, Rindler vacuum, Minkowski vacuum
Переглядів 1099 годин тому
This video is an excerpt of a course that is currently being published on Patreon. The Unruh effect reveals that an accelerated observer perceives the Minkowski vacuum as a particle-filled state. In the non-inertial frame, the definition of vacuum differs, leading to the striking realization that acceleration alters the perception of quantum states. This insight bridges quantum field theory, sp...
QUANTUM EFFECTS IN GRAVITY LEC.1: Euclidean action for a scalar field coupled to gravity
Переглядів 10414 днів тому
This is the first among a series of lectures which explore the quantum corrections to General Relativity through effective actions in curved spacetime. The series of lectures delves (among other things) into the zeta function regularization method for infinite determinants, the heat kernel formalism, and how quantum effects lead to corrections involving the Ricci scalar 𝑅 and Ricci tensor 𝑅𝜇𝜈. ...
Transformation of a vector field according to the Lorentz algebra
Переглядів 64Місяць тому
Lorentz Lie Algebra of Vectors and Spinors In the framework of the Lorentz Lie Algebra, by applying a 2π rotation of a 4-vector around the z-axis one recovers the initial vector (as expected). However, the story for spinors is fascinatingly different. Under the same 2π rotation, spinors transform to minus their initial value-a striking property that distinguishes spinors from vectors and reflec...
Considerations on operators, quantum mechanics, Schrodinger equation
Переглядів 104Місяць тому
We derive the time-dependent Schrödinger equation starting from a state and then applying a unitary transformation. 📽️ Watch the video to delve deeper into these equations. This video is also part of a course titled “Master Variational Calculus & Advanced Mathematical Methods”. #Relativity #Physics #FieldTheory #feynman #mathematics #mathematician #lovemath #mathlover #physics #physicslover #qu...
Derivation of the Lie algebra of the Lorentz group
Переглядів 98Місяць тому
In quantum theory, symmetries are represented by unitary (or anti-unitary) operators. This video dives into the derivation of the Lorentz Lie algebra and its connection to quantum scalar fields. The key topics include: ✔️ Unitary operator relations for Lorentz transformations ✔️ Derivation of commutation relations for the angular momentum and boost operators This derivation in group theory is s...
Lorentz and Poincare groups, representations, angular momentum, Lie algebras
Переглядів 227Місяць тому
Infinitesimal Poincare transformations of fields describe how physical quantities transform under translations and Lorentz transformations, forming the basis of relativistic quantum field theory. In this post, we analyze the transformation of a field with a Lorentz index, exploring its infinitesimal change, including contributions from spacetime dependence and index transformation. Using the ge...
From the path integral to the effective action, renormalization group and running of couplings
Переглядів 218Місяць тому
In quantum field theory, understanding how interactions change with energy scales is key to predicting particle behavior across different regimes. One way to do this is by examining the “effective action” at a given energy cutoff scale, denoted by Λ. At this scale, the effective action incorporates all interactions for energies below Λ, allowing us to study how particle fields behave over speci...
Functional derivatives and generalization of Euler Lagrange equations in QFT
Переглядів 585Місяць тому
Understanding Functional Derivatives in Quantum Path Integrals Functional derivatives are essential in the study of quantum path integrals, helping us calculate expectation values and make connections between classical and quantum mechanics. This example shows how setting up these derivatives can yield equations that resemble classical physics with quantum effects added. #QuantumMechanics #Path...
From Path Integrals to Perturbation Theory and then to Feynman Diagrams
Переглядів 5362 місяці тому
This video seeks to show the fundamental relationship between path integrals, perturbation theory, and Feynman diagrams. These diagrams offer an insightful graphical approach to perturbation theory, emerging seamlessly from path integral formalism. In this analysis, we expand the path integral for a particle in a potential field. Through successive expansions, each term encapsulates specific in...
How convolutions in the path integral lead to the Schrodinger equation
Переглядів 4702 місяці тому
This post delves into the path integral formulation of quantum mechanics. For a free particle, the process involves evaluating convolutions through time slices and applying the Fourier transform, leading to the derivation of the Schrödinger equation. This mathematical approach starts from the classical action to arrive at the quantum evolution. #QuantumMechanics #PathIntegrals #SchrodingerEquat...
Heuristic Derivation of Path Integrals from Classical Field Theory (including Schwinger Principle)
Переглядів 2623 місяці тому
A heuristic derivation of the path integral, starting from the Schwinger dynamical principle. This approach bridges classical field theory and quantum mechanics by considering small variations in the action. The Schwinger principle is derived by relating changes in the action to quantum transitions. This forms the foundation of the path integral formalism, where the sum over all possible field ...
Reynolds transport theorem: derivatives of time-dependent volume integrals
Переглядів 1193 місяці тому
The time derivative of a volume integral often appears in physics, particularly in the context of conservation laws and field theories. For example, in electromagnetism, the continuity equation relates the time derivative of the charge density to the divergence of the current density. The derivation shown in the video is an informal way of thinking about the transport theorem (which is related ...
Gradient in spherical coordinates (derivation using concepts of tensor calculus and linear algebra)
Переглядів 1324 місяці тому
Presented here is a detailed algorithm for computing the components of the gradient in spherical coordinates. Although this is a simple exercise usually seen in basic multivariable calculus courses, the pictures illustrate some concepts which might be inferred from tensor calculus. For further insights, refer to the accompanying video where these relations are rigorously proven and implemented ...
Derivation of the strain tensor in spherical coordinates
Переглядів 1494 місяці тому
Derivation of the strain tensor in spherical coordinates
Fourier series expansion for thin plates
Переглядів 1054 місяці тому
Fourier series expansion for thin plates
Physics of thin plates derived from the variational principle (bending and twisting moments, etc)
Переглядів 634 місяці тому
Physics of thin plates derived from the variational principle (bending and twisting moments, etc)
Classical Theory of Thin Plates derived from the Action Principle
Переглядів 1204 місяці тому
Classical Theory of Thin Plates derived from the Action Principle
Minimal surfaces in calculus of variations
Переглядів 1394 місяці тому
Minimal surfaces in calculus of variations
Markowitz Model for risk minimization in a financial portfolio
Переглядів 854 місяці тому
Markowitz Model for risk minimization in a financial portfolio
Derivation of the strain tensor in the theory of elasticity
Переглядів 1594 місяці тому
Derivation of the strain tensor in the theory of elasticity
Black Scholes equation: mathematical derivation
Переглядів 1124 місяці тому
Black Scholes equation: mathematical derivation
Interesting Fourier series in 2 dimensions
Переглядів 625 місяців тому
Interesting Fourier series in 2 dimensions
Maupertuis principle derived from the more general action principle
Переглядів 3905 місяців тому
Maupertuis principle derived from the more general action principle
Poisson brackets and analogies with Quantum Mechanics
Переглядів 2435 місяців тому
Poisson brackets and analogies with Quantum Mechanics
Calculation of Inverse Laplace Transform using residues
Переглядів 1325 місяців тому
Calculation of Inverse Laplace Transform using residues
Lorentz transformations and the Invariant Element in Special Relativity (Mathematical Derivation)
Переглядів 1305 місяців тому
Lorentz transformations and the Invariant Element in Special Relativity (Mathematical Derivation)
Intro to the Laplace Transform from the Fourier Transform
Переглядів 826 місяців тому
Intro to the Laplace Transform from the Fourier Transform





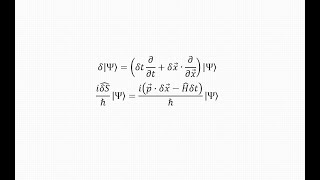



hi! love the channel. one recommendation i’d have is making more playlists i think it’d help with people finding the vids they want
These vids are quite helpful. Thank you -- and looking forward to more in the New Year. Best wishes.
I don't understrand the procedure, why do we take the dagger of the lagrangian equation?
Porque esto no es una unificación de la relatividad general con la mecánica cuántica??
With this kind of approach, we still have a semi-classical theory, because the gravitational field serves as a background for quantum fields, we have not quantized the gravitational field (in the sense that we have not computed quantum amplitudes by integrating over the metric tensor). In particular, if one dares to compute quantum amplitudes related to the gravitational field (by using the path integral for instance), it becomes impossible to remove the infinities that arise without introducing an infinite amount of couplings (this boils down to the non-renormalizability of gravity). The lecture series presented here "QUANTUM EFFECTS IN GRAVITY" aims to show that the gravitational action is affected by quantum corrections which become more and more important as we move towards the high-energy regime (high curvatures). We simply lose the predictive power of the theory with this approach.
1:00 Defined Fij as curl of magnetic potential 4-vector phi and an antisymmetric tensor. Are the two facts (chosen as curl of phi, and, antisymmetric tensor) independent, or, does one choice lead to the other?
2:00 Is the permutation equation ( del-Fij/del-xi) valid for any 4x4 tensor, or valid for any antisymmetric tensor, or valid because it was defined as curl of a 4-vector phi?
8:45 "sqrt(-g) is 1 in our frame of reference". Why? What is g? gij i guess is the metric tensor which is used to get F-upperIndex from the already defined F-lowerIndex.
@@rgudduu g represents the determinant of the metric tensor. This lecture is an excerpt taken from a section of one of my courses. That section is dedicated to Einstein's article: “The Foundation of the General Theory of Relativity”, so this video is not completely self-contained, because it uses concepts discussed in previous lectures. You might read the article or check out the course (I am not interested in selling anything, but all your questions could have "simple" answers if you dig deeper into tensors, whether you study by yourself or take whatever course you are interested in).
The "curl" should indeed be interpreted as an antisymmetric tensor, the two facts are not independent, one leads to the other.
@@rgudduu the "permutation equation" (related to Maxwell's equations) is valid for any anti-symmetric tensor written as a curl. Try to do the calculation yourself by substituting the expression of Fij written as a curl into the "permutation equation", and show that you obtain 0=0 (which means that the equation is satisfied). I have provided more details in a course related to the "covariant formulation of classical electrodynamics".
But if gxy = gyx then it would become 0=0 which makes it a identity.here we can see clearly see that to write [fdxdy]=(gxdx+gydy) Mix partial derivatives of g and f has to be 0 which makes our situation more inevitable
Not understable
It depends on your level, with some effort it can be done, to the point that this can become "easy" to understand. It's all relative
thanks for connecting lots of dots and making it a holistic explanation
how 23:36?
What that equation is telling you is that the number of particles between 𝑥 and 𝑥+𝑑𝑥 at a later time 𝑡+𝜏 depends on the displacement of neighboring particles from nearby positions at the earlier time 𝑡. Intuitively, as the displacement Δ becomes larger, the probability 𝜑(Δ) decreases, meaning that particles far from 𝑥 contribute less. Thus, the main contributions to the particle count at 𝑥 come from particles that were close to 𝑥 at time 𝑡.
Is there any book which I can refer too?
The equation seems general; what are the assumptions needed for the full expansion to converge?
convergence is a "tricky" concept when we think of path integrals. The "awesome" thing about the physics behind them is that, even if these expressions technically diverge, we can extract lots of useful information
Do you know of the Dyson-Schwinger equation?
yes, I will make a video about it soon.
Just a minor nitpick, it can get confusing if the integration variable and the integration limit use the same symbol (like "x"). I get that it works for the simplicity of writing. Love the video though.
Thanks it helped me a lot❤
wonderful explanation ! Where can i find the proof of hilbert transform for periodic function being and integral of co-tangent ?
Sir when you were able to understand all this during you academic journey... i was unaware of probability calculus till now, I am already close to finishing up my bachelors ?
“einstein derived lorentz” wait what???😮😮😮
Can I do it without complex analysis?
Some questions: 1. At 8:21, shouldn't there be a factor of 1/2? since the inner product is expanded into the sum of 2 terms 2. At 9:01, can the operator δ be treated as a constant with respect to the basis |ψ>? (since it escapes the bra-ket) 3. At 11:11, it seems like the LHS of the two equations stay the same but the RHS of the second equation got exponentiated? and I might be mistaken here, but shouldn't an integration remove all of the "δ" in the equation, including |ψ+δψ>?
1) I see what you mean. The way to interpret the action operator inside that inner product is this: the operator acts like a differential operator (on the right state, but also on the left state). Let me remind that this is a "heuristic" derivation, so the notation is not always rigorous here. Any books on QFT that deal with the Schwinger formalism should cover this more rigorously. 2) "delta" represents the variation of the state due to a small change of the field. In general, the state changes if we perturb the field, so I would not consider your interpretation correct. "delta" can act both on the "bra" and on the "ket". 3) yes, at 11:11 we have a simple exponentiation. The variable of integration on the left is the entire inner product between the "bra" and the "ket" you see in the expression. The result should be the logarithm as written in the video (the delta in the inner product does not disappear)
Another way to think about your first question. Consider the evolution of the change in the action between two states A and B. We can write the inner product: < B | δS | A >. Based upon the considerations in the video, δS should depend only on the final and initial states, so it could be written as: δS= S_B - S_A (where S_B is an operator that acts only on state B, and S_A acts only on state A). Let's assume C is another state (that you can think of as being "in between" A and B). You can write: δS = S_B - S_A = ( S_B - S_C ) + ( S_C-S_A ) Therefore: < B | δS | A > = < B | ( S_B - S_C ) | A > + < B | ( S_C - S_A ) | A > Now, those differences in the action are going to create some small perturbations. In particular, S_B - S_C will act on < B |, whereas ( S_C - S_A ) will act on | A >. This serves as another "justification" of the formula you were confused about.
I have sometimes wondered if you can write every law of physics (thermodynamics, fluid dynamics...) with differential forms.
Hey! Thank you so much for making this video. What I attempted was, I used MoC to solve for tau's PDE, and (while I don't 100% understand it yet), but realized that tau must be a function of C, and then I had a(C) just like in the paper. But then he says a = phi(v), and I'm "in general" lost about what's happening here. Secondly, I got stuck when I tried to substitute x' = x - vt back into xi, and (where gamma = lorentz factor), got a * 1/gamma^2 * (x - vt) and I got confused about what to do with the extra gamma. Then saw your video and you absorbed it into a(v), and here too I'm clueless. Can you please help /explain this? This is the only part in the derivation I'm not 100% clear on (perhaps my total lack of theoretical exploration in real analysis is the problem here), I barely managed to learn the characteristics method from youtube. Thank you so much :)
sir please recommended a book where i find this topic related examples
Holy crap. I understood your thumbnail! My flavor preferences are chocolate, vanilla, peppermint, asparagus, charm and pistachio. Up has a strange aftertaste but strange just tastes like marshmallows.
Thanks for the video. Can you please let us know a practical example how to use Reynolds transport theorem ?
In hydrodynamics you have a Eulerian picture and lagragian picture and the transport theorem is exactly the transformation between the operators between 2 pictures
More specifically if think f as density rho the theorem gives Lagrangian derivative of mass is in fact the conservation law of mass in eular picture which is the right hand side of the equation
Elegant
Thanks for this video!!!
Tricky equations 😅 but you did the job well
Wonder if the parameter nu in the constitutive relation can be linked to the conservation of mass
Yes, Poisson's ratio can indeed be linked to the concept of mass conservation. Mass conservation can be used to evaluate it. Mathematically, if a material is stretched along the x-axis, causing a strain 𝜖_𝑥, the resulting strains in the perpendicular y and z directions are given by: 𝜖_𝑦=𝜖_𝑧=−𝜈𝜖_𝑥 ν is Poisson's ratio, which is typically a positive number for most materials. Mass conservation implies that during the deformation of a material, the mass of the material remains constant. For a given volume element of the material, if we assume the material is incompressible, then its density remains constant, which implies that any increase in one dimension must be exactly compensated by a decrease in other dimensions to maintain the same volume. Consider a small cubic element of the material with an initial volume 𝑉0=𝐿𝑥 𝐿𝑦 𝐿𝑧, where 𝐿𝑥, 𝐿𝑦, and 𝐿𝑧 are the initial lengths along the 𝑥, 𝑦, and 𝑧,axes, respectively. After deformation, the new dimensions become 𝐿𝑥′=𝐿𝑥(1+𝜖_𝑥), 𝐿𝑦′=𝐿𝑦(1+𝜖_𝑦), and 𝐿𝑧′=𝐿𝑧(1+𝜖_𝑧) The new volume 𝑉′ after deformation is: 𝑉′=𝐿𝑥′𝐿𝑦′𝐿𝑧′=𝐿𝑥(1+𝜖_𝑥)⋅𝐿𝑦(1+𝜖_𝑦)⋅𝐿𝑧(1+𝜖_𝑧) For small strains, the volume can be approximated as: 𝑉′≈𝑉0(1+𝜖_𝑥+𝜖_𝑦+𝜖_𝑧) For mass conservation in the case of an incompressible material, the volume must remain constant, so 𝑉′=𝑉0 This implies: 𝜖_𝑥+𝜖_𝑦+𝜖_𝑧=0 Substituting the relationship between longitudinal and transverse strains (using Poisson's ratio): 𝜖_𝑥−𝜈𝜖_𝑥−𝜈𝜖_𝑥=0 This implies that for incompressible materials, Poisson's ratio 𝜈=1/2
@@math.physics thank you for the comprehensive explanation
Ah so the equation including W is for bending?
w(x,y) is the displacement of the generic point (x,y) of the plate in the direction z perpendicular to the plate. In the classical theory of thin plates, the derivatives of w are related to stresses, strains, bending moments, twisting moments, shear forces, etc.
🎉🎉 👏👏 🥇🏅
This equation needs alot of data 😅
Could you please explain to me why physicists before Einstein could not have arrived at the final formula?
Is it used for prediction model ?
There are several applications that demonstrate the versatility of the Black-Scholes model in the financial world, particularly in derivatives trading and risk management (I don't have much experience with that though)
nagyon jó
@@plranisch9509 köszi, azt hiszem, egy év alatt szépen fejlődtem (mármint ehhez a videóhoz képest) :)
Not following you. Where is the paper I see in the cover photo so I can just read it?
can u pls do a full review of the exam paper im in supirioe terza
Interesting problem
Bit tricky for me to understand but good explanation 🎉
How can we find length of a curve
Exuse me, I have one question. This is not really related to the topic of the video. Do you know how to plot magnetic field lines in the Schwarzschild metric in wolfram mathematica? Or do you know where i can read about this? You're my last hope :( i want to learn. Thank you in advance
🎉🎉 🏅🏅
Interesting problem
Thank you i'm watching all your videos.
The nitty grity is the most beautiful, yet doesn't appear so.
🎉🎉 🏅🏅
You are a genius, I mean it seriously, and thank you so much for your work. Really amazing and so cool to explain the Einstein theories!!!
very useful video, there's a lot of false information out there about this, falsely stating that kinetic energy in QM can be negative.
Ciao, fai anche ripetizioni? dove posso contattarti? Grazie
🎉🎉 🥇🥇🏆🏅 good content
Great proof. Please do more videos.