
- 32
- 936
Sarth
Приєднався 1 гру 2015
JEE Main 2021, Common Root Condition, Quadratic Equation PYQ
Let λ≠0
be in R.
If α
and β
are the roots of the equation x2−x+2λ=0,
and α
and γ
are the roots of the equation 3x2−10x+27λ=0,
then βγλ
is equal to ________.
be in R.
If α
and β
are the roots of the equation x2−x+2λ=0,
and α
and γ
are the roots of the equation 3x2−10x+27λ=0,
then βγλ
is equal to ________.
Переглядів: 8
Відео
JEE Main 2022 Quadratic Equation, Common Root Condition Tricky Question
Переглядів 267 годин тому
If for some p,q,r∈R , all have positive sign, one of the roots of the equation (p2 q2)x2−2q(p r)x q2 r2=0 is also a root of the equation x2 2x−8=0 , then q2 r2p2 is equal to-
JEE Main 2022 PYQ Common Root, Quadratic Equations, Algebra
Переглядів 237 годин тому
Let α , β be the roots of the equation x 2 − 4 λ x 5 = 0 and α , γ be the roots of the equation x 2 − ( 3 √ 2 2 √ 3 ) x 7 3 λ √ 3 = 0 . If β γ = 3 √ 2 , then ( α 2 β γ ) 2 is equal to
JEE PYQ Common Root Quadratic Equation
Переглядів 79 годин тому
Let a , b ∈ R be such that the equation a x 2 − 2 b x 15 = 0 has repeated root α and if α and β are the roots of the equation x 2 − 2 b x 21 = 0 , then α 2 β 2 is equal to:
Common Root Condition JEE Main PYQ
Переглядів 189 годин тому
If the value of real number α 0 for which x 2 − 5 α x 1 = 0 and x 2 − α x − 5 = 0 have a common real roots is 3 √ 2 β then β is equal to
JEE Main 2024 PYQ Limits
Переглядів 119 годин тому
Let the slope of the line 45 x 5 y 3 = 0 be 27 r 1 9 r 2 2 for some r 1 , r 2 ∈ R . Then lim x → 3 ( ∫ x 3 8 t 2 3 r 2 x 2 − r 2 x 2 − r 1 x 3 − 3 x d t ) is equal to .
JEE Main 2024 Limit Plus Newton Leibnitz Plus Binomial Plus Common Root Multi Concept PYQ
Переглядів 1549 годин тому
Let a be the sum of all coefficients in the expansion of ( 1 - 2 x 2 x 2 ) 2023 ( 3 − 4 x 2 2 x 3 ) 2024 and b = lim x → 0 ( ∫ x 0 log ( 1 t ) t 2024 1 d t x 2 ) . If the equations c x 2 d x e = 0 and 2 b x 2 a x 4 = 0 have a common root, where c , d , e ∈ R , then d : c : e equals
JEE Mains 2024 PYQ Newton Leibnitz Theorem Plus Maxima Minima
Переглядів 612 годин тому
Let S=(−1, ∞) and f:S→R be defined as f(x)=x∫−1 (et−1)11(2t−1)5(t−2)7(t−3)12(2t−10)61dt . Let p= Sum of square of the values of x, where f(x) attains local maxima on S. and q=Sum of the values of x, where f(x) attains local minima on S. Then, the value of p2 2q is
Matrix Equation 2 Order JEE PYQ. Solve within seconds. Shortcut Matrix
Переглядів 512 годин тому
Matrix Equation 2 Order JEE PYQ. Solve within seconds. Shortcut Matrix
Matrix Equation 3 Order Shortcut JEE PYQ 2024
Переглядів 1214 годин тому
Matrix Equation 3 Order Shortcut JEE PYQ 2024
Matrix Equation Shortcut JEE PYQ 2024
Переглядів 1514 годин тому
Matrix Equation Shortcut JEE PYQ 2024
Dot Product Vector Algebra JEE 2024 PYQ
Переглядів 1014 годин тому
Dot Product Vector Algebra JEE 2024 PYQ
JEE Advanced 2023 PYQ Newton Leibnitz Theorem Plus Differential Equation
Переглядів 1816 годин тому
JEE Advanced 2023 PYQ Newton Leibnitz Theorem Plus Differential Equation
JEE PYQ 2024 8 April Shift 1 Binomial Coefficient Series
Переглядів 1719 годин тому
JEE PYQ 2024 8 April Shift 1 Binomial Coefficient Series
Binomial Coefficient Series JEE 2023 PYQ
Переглядів 1019 годин тому
Binomial Coefficient Series JEE 2023 PYQ
Binomial Coefficient Series JEE 2023 PYQ
Переглядів 1419 годин тому
Binomial Coefficient Series JEE 2023 PYQ
Binomial Coefficient Series IIT JEE Main 2024 PYQ
Переглядів 1621 годину тому
Binomial Coefficient Series IIT JEE Main 2024 PYQ
Arithmetico Geometric Progression JEE PYQ 2024
Переглядів 94День тому
Arithmetico Geometric Progression JEE PYQ 2024


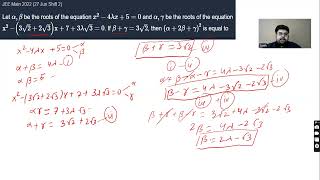






Very very nice excellent❤❤❤❤❤
👍
Excellent
Excellent explanation
❤
Excellent
Excellent
Excellent Sir
❤
❤
😄👍👍👍👍
Excellent explanation❤
Veri good
❤
❤
Excellent❤❤❤❤❤
❤
Excellent explanation
❤
Excellent explanation❤
❤
😊👍👍👍
Super❤
Very very nice
Bahut Achcha Tarika Hai padhaane ka
❤
❤
Great 👍👍👍
❤
Nice explanation
😀👍👍👍👍👍
❤
Veri good Sar
❤
Great Sir.
Bhai bahut healthy ho gaya hai ❤
helpful sir
Very good 👍 👍
Nice sir
Nice... Very informative sir...
Very useful
Nice explanation sir...😊
help ful sir
👍💯
👍💯