- 5
- 119 311
Chalk Talk
Приєднався 9 чер 2022
Math, computer science, physics, etc.
Made by Kelsey Houston-Edwards
www.kelseyhoustonedwards.com
Made by Kelsey Houston-Edwards
www.kelseyhoustonedwards.com
Learning with errors: Encrypting with unsolvable equations
Learning with errors scheme.
This video uses only equations, but you can use the language of linear algebra (matrices, dot products) to discuss lattices and learning with errors. Check out the resources below for more information.
Created by Kelsey Houston-Edwards (www.kelseyhoustonedwards.com)
Sponsored by Wire (www.wire.com)
________
Post-Quantum Cryptography: ua-cam.com/video/_C5dkUiiQnw/v-deo.html
Lattice-Based Cryptography: ua-cam.com/video/QDdOoYdb748/v-deo.html
________
Timestamps
0:00 - Introduction
0:35 - Learning without errors
1:58 - Introducing errors
3:36 - Modular arithmetic
3:59 - Encrypting 0 or 1
7:14 - Relationship to lattices
________
Modular arithmetic (wiki): en.wikipedia.org/wiki/Modular_arithmetic
Modular arithmetic (Khan Academy): www.khanacademy.org/computing/computer-science/cryptography/modarithmetic/a/what-is-modular-arithmetic
Modular arithmetic (video, blackpenredpen): ua-cam.com/video/6dZLq77gSGU/v-deo.html
LWE (expository notes): cims.nyu.edu/~regev/papers/lwesurvey.pdf
LWE (lecture): ua-cam.com/video/K_fNK04yG4o/v-deo.html
Encryption from LWE (lecture notes): courses.grainger.illinois.edu/cs598dk/fa2019/Files/lecture10.pdf
Kyber (website): pq-crystals.org/kyber/index.shtml
This video uses only equations, but you can use the language of linear algebra (matrices, dot products) to discuss lattices and learning with errors. Check out the resources below for more information.
Created by Kelsey Houston-Edwards (www.kelseyhoustonedwards.com)
Sponsored by Wire (www.wire.com)
________
Post-Quantum Cryptography: ua-cam.com/video/_C5dkUiiQnw/v-deo.html
Lattice-Based Cryptography: ua-cam.com/video/QDdOoYdb748/v-deo.html
________
Timestamps
0:00 - Introduction
0:35 - Learning without errors
1:58 - Introducing errors
3:36 - Modular arithmetic
3:59 - Encrypting 0 or 1
7:14 - Relationship to lattices
________
Modular arithmetic (wiki): en.wikipedia.org/wiki/Modular_arithmetic
Modular arithmetic (Khan Academy): www.khanacademy.org/computing/computer-science/cryptography/modarithmetic/a/what-is-modular-arithmetic
Modular arithmetic (video, blackpenredpen): ua-cam.com/video/6dZLq77gSGU/v-deo.html
LWE (expository notes): cims.nyu.edu/~regev/papers/lwesurvey.pdf
LWE (lecture): ua-cam.com/video/K_fNK04yG4o/v-deo.html
Encryption from LWE (lecture notes): courses.grainger.illinois.edu/cs598dk/fa2019/Files/lecture10.pdf
Kyber (website): pq-crystals.org/kyber/index.shtml
Переглядів: 29 039
Відео
Lattice-based cryptography: The tricky math of dots
Переглядів 47 тис.Рік тому
Lattices are seemingly simple patterns of dots. But they are the basis for some seriously hard math problems. Created by Kelsey Houston-Edwards (www.kelseyhoustonedwards.com) Sponsored by Wire (www.wire.com) Post-Quantum Cryptography: ua-cam.com/video/_C5dkUiiQnw/v-deo.html Learning with Errors: Coming January 5, 2023 Timestamps 0:00 - Post-quantum cryptography introduction 0:58 - Basis vectors...
Post-quantum cryptography: Security after Shor’s algorithm
Переглядів 20 тис.Рік тому
What’s the current status of the NIST Post-Quantum Cryptography Standardization? Find out here: csrc.nist.gov/Projects/Post-Quantum-Cryptography Created by Kelsey Houston-Edwards (www.kelseyhoustonedwards.com) Sponsored by Wire (www.wire.com) Lattice-Based Cryptography: ua-cam.com/video/QDdOoYdb748/v-deo.html Learning with Errors: Coming Jan 5, 2023 Timestamps 0:00 - National Institute of Stand...
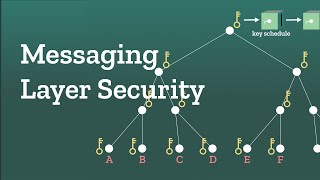
Messaging layer security: Encrypting a group chat
Переглядів 10 тис.2 роки тому
How do you keep the messages in a group chat secure? Messaging layer security (MLS). The Double Ratchet algorithm provides end-to-end encryption for text messages between two people. But securing a group chat is much harder. MLS is the first standardized multi-party “key exchange” - a protocol for communication among groups of people or devices. Resources: Video on the Double Ratchet algorithm:...
Double ratchet algorithm: The ping-pong game encrypting Signal and WhatsApp
Переглядів 13 тис.2 роки тому
How do text messaging services like Signal and WhatsApp keep your text messages secure? The Double Ratchet algorithm. Let’s say Alice wants to send Bob an end-to-end encrypted message. She uses a key to lock up the message and Bob uses the same key to unlock the message. But what if they want to send a bunch of messages back and forth? Using the same key the whole time is not very secure. It wo...
Why was I not notified you had this channel... bad youtube algorithm!
Leannon Harbors
9539 Blair Landing
It would be great to see more Americans involved in the tech industry. Imagine the same presentation from someone from India!
1016 Lemuel Point
05488 Nova Turnpike
What happened? Where are youu?
Hertha Expressway
8474 Laisha Oval
Dicki Street
Ima Lock
7351 Brennon Mission
This is a lattice? cdn.britannica.com/77/170677-050-F7333D51/lettuce.jpg
Sarina Road
Why can't you use the bad basis to make another good basis and use that to solve the closest vector problem?
Keeling Drives
4034 Walter Estates
Make more videos!!!
Thank you so much for your work, I would love to see more videos on the current NIST encryptions standards.
Hold on there my math senses tingling by the very definition of the whole number lattice that you’ve described in these examples doesn’t that mean that while it may take infinite steps to reach somewhere every whole number point on the plane or in the quote unquote probability phase space is reachable so any whole number coordinate is a valid solution. Therefore, the closest or shortest vector is one whole number unit away and thiswould hold true for n dimensions.
Thanks great vid
Great video, thanks Kelsey; subscribed.
Brilliantly explained..Thanks
she just broke my brain and my encryption 😂
Why stop posting?? When u have good presenting skills and knowledge
All of these videos are brilliant.
So well communicated. Excellent.
hopefully you create more of this great content!
This is a phenomenal video. Thank you so much for take the time to clearly explain a complex topic. I'm very grateful for your work!
Why can't the bad basis simply be orthonormalized?
best series of videos that explain lattice based crypto for masses.
How could Bob create the list of all lattice points using bad basis? If everyone having bad basis can create the lattice, what is stopping them from finding the closest lattice point just by visual inspection?
Really thankful for this explaination ❤️
the best explanation of lattice in youtube 🔥
nice work! thanks : )
What an amazing explanation!!! I believe you should teach Mathematicians how to teach!
noooooooooooo why are you gone again?!? why did I not find the channel earlier? whhhhhy edit: oh, I am so sad
This video is so cool 😎 thx
Well-articulated! Thank you.
Well-articulated! Thank you.
Well-articulated! Thank you.
This only works with very short messages. It’s not generalizable to, say, a one page letter. It’s equivalent to sending a blurry image that the recipient can sharpen but so could a mitm. I’m not so sure this is as unsolvable as you think, and if it were, both Alice and Bob would need a way to share the actual errors securely in the future.
such a beautifully well done video. Thank you for taking an intimidating concept and making it accessible.
this was amazing!
very pleasant to watch.
What about AES 256?
that is also vulnerable
@@neuekatze1 I don't think so. It will still offer 128 Bits of security which is still very high.
5:15 but couldnt malkob(bobs bully) just calculate that 30x+67y+53z+24w=19(mod 89) is 0 and then check if it is equal to 0
Very clear explanation! Thank you!
Thank you so much. It's so simple and understandable
It is unclear how F gets its private key at 6'16''. It is also unclear why the rachet can go up the tree as well as down the tree.
It’s a bit confusing in the graphics but F must derive its own Public Private key pairs itself first, give Alice the public key, then Alice will wrap the group secrets (tree private keys) with Franks public key so that F can join the group chat. F gets its welcome message directly from Alice. Basically you can use any method to give F the welcome message.
Also think of the ratchet as the “propagation path” for a new key. The ratchet doesn’t HAVE to go unidirectional on the tree. The ratchet is in the direction of any new key that’s being propagated.