Відео

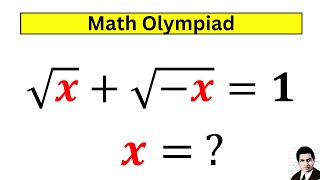
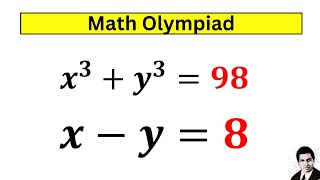
Where did m=2 comes from?

x + xy + y = 54 x + xy + y + 1 = 54 + 1 x(1 + y) + (y + 1) = 55 (y + 1)(x + 1) = 55 (y + 1)(x + 1) = 5.11 y + 1 = 5 y = 4 x + 1 = 11 x = 10 x + y = 14

Please check, the positive solution is not valid.

x=z+4 & y=z-4; (z+4)^3+(z-4)^3=2(z^3+48z)=98; z^3+48z-49=0. By inspection z=1. x+y=2z=2.

(x,y)=(7,5) or(-7,-5) or (5i,-7i)

I can answer immediately. Then I showed my work. I factored (x^2 - y^2) into (x + y)(x - y), which may not have been necessary. I used the quadratic formula, which takes longer than factoring by grouping, but it worked.

Nice problem. Similarly... Let u = a² and v = b². Find z = a³ + b³ u + v = 28 u² + v² = 584 (u + v)² = 584 - 2uv or uv = ((u + v)² - 584)/2 = (28² - 584)/2 = 100 (u + v)³ = u³ + v³ + 3uv(u+v) or u³ + v³ = (u + v)³ - 3uv(u+v) = 28³ - 3•100•28 = 13,552 z² = (a³ + b³)² = a⁶ + 2a³b³ + b⁶ = u³ + v³ + 2(√(uv))³ = 13,552 + 2,000 = 15,552 z = 72√3 ----------------- in general if a² + b² = c₁ and a⁴ + b⁴ = c₂ then a³ + b³ = √[ c₁(3c₂ - c₁²)/2 - 2(√[ (c₁² - c₂)/2] )³ ]

Easy solution method. Substitute x=y+2 and rearrange to 2*4*2*y(y^2+4)=0, which yields y=0 & y=±2i, and x=2+y=2 & x=2±2i.

Let y = 2x/(x+2) then x^2+y^2 = 5 & 2 x - 2 y = xy squaring both sides 20 - 8 xy = (xy)^2 xy = 2 , -10 case 1 xy = 2 x^2 - x - 2 = 0 x = - 1 , 2 case 2 xy = - 10 x^2+5x+10 = 0 x = (- 5 + i√15)/2 , (- 5 - i√15)/2

So STUPID, what ia the CRAZY answer and miss leading JUNK 🖤🖤🖤🖤

x - y = 17 (1) √x + √y = 17 (2) x = 81 y = 64 x = (√x)^2 y = (√)^2 x - y = 17 (√x)^2 - (√y)^2 = 17 (√x+√y).(√x-√y) = 17 17.(√x-√y) = 17 √x - √y = 1 (3) 2 e 3 √x + √y = 17 √x - √y = 1 ------------------- 2√x = 18 √x = 9 x = 81 (1) x - y = 17 81 - y = 17 y = 64

Well that was a waste of time watching something absolutely of no use in real life.

You made a mistake during your last quadratic. C was -2 but you put +2. Your final answer is less complicated if you fix this

👍

Draw a circle of radius |a| centered on the origin of the complex plane. Mark a=|a|i at the top of the circle and -a=-|a|i at the bottom of the circle where a>0 is real. Then √a=√|a|(√2/2)(1+i) & √(-a)=√|a|(√2/2)(1-i) and √a+√(-a)=√|a|√2=4. Squaring both sides gives 2|a|=16 or |a|=8 and a=8i. Check: √(8i)=√8*√i=2√2(√2/2)(1+i) and √(-8i)=√8*√(-i)=2√2(√2/2)(1-i). √(8i)+√(-8i)=2√2(√2/2)(1+i)+2√2(√2/2)(1-i)=2+2=4.

Is this a olympiad level question?like seriously?

This question frightened 300K+ examiners: m³ + 11m = 30; m =? m³ + 11m - 30 = 0, (m³ - 2³) + (11m - 22) = 0 (m - 2)(m² + 2m + 4) + 11(m - 2) = (m - 2)(m² + 2m + 15) = 0 m - 2 = 0; m = 2 or m² + 2m + 15 = 0, (m + 1)² = - 14 = (i√14)²; m = - 1 ± i√14 Answer check: m = 2: m³ + 11m = 2³ + 11(2) = 8 + 22 = 30; Confirmed m = - 1 ± i√14: m² + 2m + 15 = 0, m² = - 2m - 15 m³ = - 2m² - 15m = - 2(- 2m - 15) - 15m = 30 - 11m, m³ + 11m = 30; Confirmed Final answer: m = 2; Two complex value roots, m = - 1 + i√14 or m = - 1 - i√14

NICE

NICE

Thanks

Substitute x=y-1/2 into the given equation and rearrange to (y^2-1/4)(y^-9/4)-48/16=(y^2)^2-(10/4)y^2-39/16=0 y^2=[(5/2)±(8/2)]/2=13/4 or -3/4. y=±√13/2 or ±i√3/2 and x=(-1±√13)/2 or (-1±i√3)/2

The equation to solve is (1) m³ + 11m = 30 Of course you can start by bringing the constant from the right hand side over to the left hand side, but it will not be clear to many beginning students why you would then split up 30 into 8 + 22 to proceed. It is clear that the left hand side of (1) is _strictly increasing_ on the real number line, which implies that this equation can only have _one real solution_ meaning that its other two solutions will be complex. We can start looking for rational solutions using the _rational root theorem_ which guarantees that any potential rational solution of (1) must be an _integer_ which is a divisor of the constant term 30. Moreover, we can see that the left hand side is _negative_ for any negative value of m, so (1) cannot have any negative real solutions and _a fortiori_ not any negative integer solutions. Therefore, we only need to test the positive divisors of 30, which are 1, 2, 3, 5, 6, 10, 15, 30. Then, we quickly find that m = 2 is a solution since (2) 2³ + 11·2 = 30 Now, since both sides of (2) are equal, we can subtract (2) from (1) to get (m³ − 2³) + 11(m − 2) = 0 where the two terms at the left hand side have a common factor (m − 2) which we can take out to get (m − 2)(m² + 2m + 2² + 11) = 0 Of course, the complete solution of this cubic equation is now easy and can proceed as shown in your video.

Why not 25 squared while squaring x-y

Add required to the main problem.It was misleading to find x+y or x,y..

√x=25/2+z and √y=25/2-z; (25/2+z)^2-(25/2-z)^2=50z=25; z=1/2 x=(25/2+1/2)^2=13^2=169; y=(25/2_1/2)^2=144

√(25(5+√24))=5√(5+√24)=5√(2+3+2√2√3)=5√(√2+√3)²=5(√2+√3)

The equation to solve is 4x⁴ + 3x³ − 2x² + 3x + 4 = 0 This is a palindromic quartic equation. Of course I am familiar with the method you demonstrate for solving palindromic equations by converting this into a quadratic in x + 1/x, but for quartic palindromics I prefer completing the square twice, which is closely related to Ferrari's method for solving quartics in general. This does not require a substitution. Here is how I would solve this equation: 4(x⁴ + 1) + 3x(x² + 1) − 2x² = 0 4(x⁴ + 2x² + 1) + 3x(x² + 1) − 10x² = 0 4(x² + 1)² + 3x(x² + 1) − 10x² = 0 (2(x² + 1))² + 2·2(x² + 1)·(³⁄₄x) + (³⁄₄x)² − (³⁄₄x)² − 10x² = 0 (2(x² + 1) + ³⁄₄x)² − ¹⁶⁹⁄₁₆x² = 0 (2x² + ³⁄₄x + 2)² − (¹³⁄₄x)² = 0 (2x² + ³⁄₄x + 2 + ¹³⁄₄x)(2x² + ³⁄₄x + 2 − ¹³⁄₄x) = 0 (2x² + 4x + 2)(2x² − ⁵⁄₂x + 2) = 0 2x² + 4x + 2 = 0 ⋁ 2x² − ⁵⁄₂x + 2 = 0 x² + 2x + 1 = 0 ⋁ 64x² − 80x + 64 = 0 (x + 1)² = 0 ⋁ (8x − 5)² = −39 x = −1 ⋁ x = (5 + i√39)/8 ⋁ x = (5 − i√39)/8

Change 11 as 9 or,20 as 30.

Why mn is 30 if it was given 20.

My solution, before watching your video: (x + 2)(x + 3)(x + 4)(x + 5) = (x − 2)(x − 3)(x − 4)(x − 5) (x² + 7x + 10)(x² + 7x + 12) = (x² − 7x + 10)(x² − 7x + 12) (x² + 7x + 11 − 1)(x² + 7x + 11 + 1) = (x² − 7x + 11 − 1)(x² − 7x + 11 + 1) (x² + 7x + 11)² − 1² = (x² − 7x + 11)² − 1² (x² + 7x + 11)² − (x² − 7x + 11)² = 0 ((x² + 7x + 11) − (x² − 7x + 11))((x² + 7x + 11) + (x² − 7x + 11)) = 0 14x(2x² + 22) = 0 x(x² + 11) = 0 x = 0 ⋁ x² + 11 = 0 x = 0 ⋁ x = 11i ⋁ x = −11i

this solution is wrong. (x-3)^4=7^4 --> 4th root of each side is equal thus x-3=7 --> x=10 and as we must have +- of the roots it;s +-10

((x-3)^2)^2-(7^2)^2=0 , (x^2-6x+9+49)(x^2-6x+9-49)=0 , (x^2-6x+58)(x^2-6x-40)=0 , x= 3+7i , 3-7i , 10 , -4 , I liked the task!

The equation to solve is x² + (3x/(x − 3))² = 16 Since (x − 3)² = x² − 6x + 9 we have x² = (x − 3)² + 6x − 9 so we can rewrite the equation as (x − 3)² + 6x − 9 + (3x/(x − 3))² = 16 Adding 9 to both sides gives (x − 3)² + 6x + (3x/(x − 3))² = 25 Now observe that the left hand side is a perfect square a² + 2·a·b + b² = (a + b)² with a = x − 3 and b = 3x/(x − 3) since 6x = 2·(x − 3)·(3x/(x − 3)) = 2·a·b is twice the product of a = x − 3 and b = 3x/(x − 3) and also note that 25 = 5² so we can write the equation as ((x − 3) + (3x/(x − 3))² = 5² Applying the equal squares property A² = B² ⟺ A = B ⋁ A = −B this gives (x − 3) + (3x/(x − 3) = 5 ⋁ (x − 3) + (3x/(x − 3) = −5 Multiplying both sides of both these equations by x − 3 to get rid of the fractions this gives (x − 3)² + 3x = 5(x − 3) ⋁ (x − 3)² + 3x = −5(x − 3) x² − 6x + 9 + 3x = 5x − 15 ⋁ x² − 6x + 9 + 3x = −5x + 15 x² − 8x + 24 = 0 ⋁ x² + 2x − 6 = 0 Completing the square for both these quadratic equations gives (x − 4)² − 16 + 24 = 0 ⋁ (x + 1)² − 1 − 6 = 0 (x − 4)² = −8 ⋁ (x + 1)² = 7 (x − 4)² = (2i√2)² ⋁ (x + 1)² = (√7)² and again applying the equal squares property to both these equations we have x − 4 = 2i√2 ⋁ x − 4 = −2i√2 ⋁ x + 1 = √7 ⋁ x + 1 = −√7 x = 4 + 2i√2 ⋁ x = 4 − 2i√2 ⋁ x = −1 + √7 ⋁ x = −1 − √7 and the equation is solved.

(0+2+4+6)/4=3. Substitute x=y-3 into the given equation and express as (y^2-1)(y^2-9)-9=y^4-10y^2=0. Thus, y^2=0 & y^2=10 and x=-3 twice & x=-3±√10

just use quadratic formula

6=x+(1/x)+x²+(1/x)²+x³+(1/x)³ Scrutinizing x=1 Algebraically, let x+(1/x)=u x²+(1/x)²=[x+(1/x)]²-2 =u²-2 x³+(1/x)³=[x+(1/x)]³-3[1+(1/x)] =u³-3u Therefore 6=u+u²-2+u³-3u u³-8+u(u-2)=0 (u-2)(u²+2u+4+u)=0 u=2 --> x+(1/x)=2 x²-2x+1=0 --> x=1 u³+3u+4=0 which is positive defiinite

xsqrt(x)+sqrt(x)=10 (x+1)sqrt(x)=2×5 [{sqrt(x)}²+1]sqrt(x)=2×(2²+1) sqrt(x)=2 --> x=4

sqrt(x)+sqrt(-x)=2 Squaring: x+2sqrt(-x²)+(-x)=2 2xsqrt(-1)=2 xi=1 --> x=1/i =-i

Simple ! Find Log on base 10 for 54 divide by log 3 on base 10! Look in log tables and you have solution! If you are after numerical answer!

I dont even understand your language, yet I was able to follow your instructions. Thank you for this video, helped me a lot

sqrt(x+1)+1-sqrt[(x-1)/x]=0 sqrt(x+1)=-1+sqrt[(x-1)/x] Squaring: x+1=1+[(x-1)/x]-2sqrt[(x-1)/x] x=[(x-1)/x]-2sqrt[(x-1)/x] Multiply by x: x²=(x-1)-2xsqrt[(x-1)/x] =(x-1)-2sqrt[x(x-1)] Put all terms in one side: (x²-x)+2sqrt(x²-x)+1=0 a quadratic equation in sqrt(x²-x) [sqrt(x²-x)+1]²=0 --> sqrt(x²-x)=-1 Squaring x²-x-1=0 x=½[1±sqrt(5)) Noting that 0<x=<1, x=½[1-sqrt(5)]

The question is badly written. The dot for multiplication sign looks like a decimal point.

√9 + √8 √9 = 3 √8 = 2√2 3 + 2√2 √(a + b)^2 = √a^2+b^2+2ab 2ab = 2√2 ab = √2 a^2 + b^2 = 3 > √2.√1 = √2 a = √2 b = √1 = 1 (√2)^2 = 2 2 + 1 = 3 √(√2+1)^2 √2 + 1

As per the thumbnail, the question isn't for me so I didn't solve it 😂😂❤❤

Msc level quadratic equations lao yr Tab ayega maza 😎

(X-1/2)² krne pe ye equation mil jayega

Rehan de bhai ... (.x/5)^ x= 5 ^ 25 Compare power n base both gives x= 25 Fastest ..

(x/5)^x = 5^5^2 (x/5)^x = 5^25 x/5 = 5 x = 25 (25/5)^25 = 5^25 5^25 = 5^25 x = 25

Y=X^2+1, X(Y-2X)/（Y^2+X^2-2XY）=2/9， 9XY-18X^2=2X^2+2Y2-4XY，20X^2-13XY+2Y2=0， （4X-Y）（5X-2Y）=0

Y^3+5=Y^3+Y^2-5Y-（Y2+Y-5）+6Y=6Y，X+5/Sqrt（X）=Y^2+5/Y=（Y^3+5）/Y=6Y/Y=6