
- 16
- 19 450
EJ Falconi
United States
Приєднався 28 вер 2022
Videos related to math, economics, philosophy, and computer science mostly.
Is mathematics a product of our perception of time?
In this video, I attempt to explain the philosophy of mathematics known as intuitionism, which was introduced by Dutch mathematician L.E.J. Brouwer.
0:00 Intro
1:01 First Act of Intuitionism
2:58 Intuitionism's objection to the Law of the Excluded Middle
4:38 Proof of Negation vs Proof by Contradiction
6:00 Second Act of Intuitionism (choice sequences)
7:46 Lawlike vs lawless
9:53 Brouwer vs Hilbert
10:24 Conclusion
Music used:
The Dark Glow of the Mountains by Chris Zabriskie is licensed under a Creative Commons Attribution 4.0 license. creativecommons.org/licenses/by/4.0/
Source: chriszabriskie.com/darkglow/
Artist: chriszabriskie.com/
Thanks for watching.
#brouwer #philosophyofmathematics #logic #nominalism #realism #intuitionisticlogic
0:00 Intro
1:01 First Act of Intuitionism
2:58 Intuitionism's objection to the Law of the Excluded Middle
4:38 Proof of Negation vs Proof by Contradiction
6:00 Second Act of Intuitionism (choice sequences)
7:46 Lawlike vs lawless
9:53 Brouwer vs Hilbert
10:24 Conclusion
Music used:
The Dark Glow of the Mountains by Chris Zabriskie is licensed under a Creative Commons Attribution 4.0 license. creativecommons.org/licenses/by/4.0/
Source: chriszabriskie.com/darkglow/
Artist: chriszabriskie.com/
Thanks for watching.
#brouwer #philosophyofmathematics #logic #nominalism #realism #intuitionisticlogic
Переглядів: 6 069
Відео
What if all of mathematics is just an elaborate fiction?
Переглядів 7 тис.Місяць тому
In this video, I attempt to explain the philosophy of mathematical fictionalism, which is a type of mathematical nominalism. 0:00 Intro 0:23 Explaining mathematical fictionalism 2:48 Hartry Field and Science Without Numbers 5:04 A motivation of fictionalism 6:01 Fictionalism's challenges 7:20 An upside to fictionalism 8:00 Conclusion Credits: ua-cam.com/video/L0xM_vLtaqg/v-deo.html ua-cam.com/v...
Does the number two exist?
Переглядів 1 тис.2 місяці тому
In this video, I attempt to explain the philosophies of mathematical realism and moderate realism. I also explain what the The Quine-Putnam Indispensability Argument is. 0:00 Mathematical Platonism/Realism 3:09 Moderate/Aristotelian Realism 5:23 Quine-Putnam Indispensability Argument 7:11 Support for QPIA: Naturalism and Confirmational Holism 9:04 Conclusion #philosophyofmathematics #philosophy...
Solving an Initial Value Problem Using Separation of Variables (Example with Inverse Tangent)
Переглядів 29Рік тому
In this video, we solve an ODE IVP using the method of separation of variables. #mathematics #calculus #differentialequation
Solving an ODE Using Separation of Variables (Example with Long Division)
Переглядів 45Рік тому
I show you how to solve an ODE using separation of variables. What's the trick here? #mathematics #calculus #integration
Axioms of Rational Choice | Economics
Переглядів 278Рік тому
In this video, I talk about the three axioms of rational choice: completeness, transitivity, and continuity. 0:00 Intro 0:34 Completeness 1:26 Transitivity 2:09 Continuity 3:39 Conclusion #economics #rationalchoicetheory #mathematics #logic
Abstract Algebra | Binary Operations, Binary Structures, & Isomorphism
Переглядів 1,2 тис.Рік тому
In this video, I try to explain what are binary operations, binary algebraic structures, and isomorphisms. Thanks for watching. Music used: Breakfast in Paris by Alex-Productions | onsound.eu/ Music promoted by www.chosic.com/free-music/all/ Creative Commons CC BY 3.0 creativecommons.org/licenses/by/3.0/ #abstractalgebra #isomorphism #mathematics
Codomain, Image, Range and Pre-image Explained | Functions
Переглядів 3,6 тис.Рік тому
In this video, I try to explain the difference among the following: codomain, image, range, and preimage. Thanks for watching. Music used: Breakfast in Paris by Alex-Productions | onsound.eu/ Music promoted by www.chosic.com/free-music/all/ Creative Commons CC BY 3.0 creativecommons.org/licenses/by/3.0/ #codomain #functions #mathematics
Set Theory | Equivalence Relations Explained
Переглядів 134Рік тому
In this video, I try to explain what are equivalence relations. Music used: Wild Strawberry by Purrple Cat | purrplecat.com/ Music promoted on www.chosic.com/free-music/all/ Creative Commons Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0) creativecommons.org/licenses/by-sa/3.0/ #equivalencerelations #settheory #mathematics
Set Theory | Injection, Surjection, and Bijection Explained | Functions
Переглядів 208Рік тому
In this video, I try to explain injection, surjection, and bijection. Thanks for watching. Music used: Breakfast in Paris by Alex-Productions | onsound.eu/ Music promoted by www.chosic.com/free-music/all/ Creative Commons CC BY 3.0 creativecommons.org/licenses/by/3.0/ #surjection #bijection #mathematics
Calculus | Preservation of Inequality Explained
Переглядів 149Рік тому
In this video, I try to explain what the Preservation of Inequality is in calculus, and why it's important. Music used: Wild Strawberry by Purrple Cat | purrplecat.com/ Music promoted on www.chosic.com/free-music/all/ Creative Commons Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0) creativecommons.org/licenses/by-sa/3.0/ #calculus #preservationofinequality #mathematics
Calculus | Intermediate Value Theorem Explained
Переглядів 251Рік тому
In this video, I explain the Intermediate Value Theorem, as simply as possible. Music used: Wild Strawberry by Purrple Cat | purrplecat.com/ Music promoted on www.chosic.com/free-music/all/ Creative Commons Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0) creativecommons.org/licenses/by-sa/3.0/ #calculus #intermediatevaluetheorem #mathematics
Calculus | The Formal Definition of a Limit Explained
Переглядів 345Рік тому
Calculus | The Formal Definition of a Limit Explained



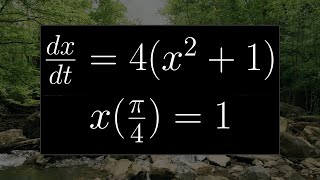





Have to love the meaningless philosophical babble.
I've always taken issue with the "every digit is a chioce" interpretations of math, because you can prove that the expansion in base 6 of 2/5 is 0.222... repeating and that any deviation from that infinite series gives you the wrong answer. You can get the entire number in 0.4 in base 10, but suddenly you comsider the fact that the reals might exist and 0.4000000... becomes an infinite series of choices? This just isn't how people think of the number 0.4.
Beautiful video. Thanks for sharing ❤. Lately I’ve been pondering a lot about the effect of our perception of time in our worldview and this great video came at the right time.
To P or to not-P? Thats the actual question lol
Once great happiness come substantial positive exponents and fantastic. Thank you with many proportion.
3:32 that seems to imply the meaning of truth is undecided
Its the opposite project of Frege, Husserl, Hilbert. But language has been understood to be possible if there are innate structures. This means a monkey s possibility of speaking with its hands its limited. Robin Williams saw Koko a gorilla, he already had inaugurated and patented 🖖 a greeting, a character that spoke an alien language, but this language has a physical counterpart. And yes we can see black holes and inconmensurable parts of them, but they are beyond our capacity to process them, even if we have them in presence as a "whole/part". Realities that seemed mathematical artifacts turned with gravitational waves true physical phenomena. Any physical object is not present as a whole. Its open to future investigations. So i dont have a posture in a realm thats not mine. Thanks for the videos!!
Mathematics and all that man create are artifice, no matter how strong it’s illusion, and will one day to crumble in to the sands of a forgotten empire. As Ozymandious wept so to will aA creatures, great and small learning still to place importance on such temporal interests.
It's blowing my mind that people think humans invented math, it's really not true, aliens would have the same mathematics but with different notations. When you do math, you really don't decide what happens, the concepts are already there and you can't change them, wether you want it or not. All you can do is see them or not see them.
Apparently as an intuitionist all real valued functions are continuous. This may not be very useful?
Time I.S. Information System timing our thought processes. 010
Intuitionistic logic is just another logic system like propositional calculus except good for types
If numbers are the product of a process, as such, then the numbers you are talking about are not the real numbers. They're just rational numbers. And it's certainly sensible to make the claim that real numbers don't exist, for it's impossible to reference unambiguously any real number that doesn't fall in a stricter category. But I would argue that even if you don't believe real numbers exist due to the intuitionist perspective, there are many irrational and transcendental numbers that still do exist. As you mentioned, there are processes that unambiguously reference Pi. Pi is not the digits that result from a finite expansion of that process, but the process is an unambiguous reference to the true nature of Pi. You can apply algebra to the limit behavior of the process, and maintain a consistent and logical system. Furthermore, the conclusions that result from these systems have sensible and applicable value to real world engineering, so that's further evidence that these systems have truth value. But for the other 100% of real numbers that don't fall into a stricter category, you can't unambiguously reference a single one. You can't do algebraic manipulation on something you can't reference. So you can't draw conclusions about specific examples. So for all practical purposes, these numbers might as well not exist.
Regardless of whether some P can or can't be proven or disproven by, the fact remains: Given P, P is either P or ¬P There isn't a third ontological category. (Sorry for my informal notation😅) ...Why the prioritization of the human perspective of P? Are you (the intuitionalists) saying that what makes a thing to be is whether we perceive it? This makes nonsense of the coherence of our perception. How can there be consistency in the things we observe, and especially what we observe in common, if perception is prior to object perceived? Why isn't consciousness always as incomprehensible as an acid trip?
✨pwahcess✨
This is danger matter for our laws and all our opinion and belief made systems, its obious the ilusions like good and evil are just made up by us but is humanity ready for thar huge pill
Mathematical processes, like all processes, are based on motor programs in the motor cortex, linked to the conscious frontal cortex through the prefrontal cortex. So are counting and time..Also infinity. Potential infinity is like walking without a termination test without an end state. Actual infinity has a forced end state. Motor programs can be nested, but there's a limit. I can understand transfinites up to א 4 but that's about it. Boolean logic is in a different area, the topographic maps (terrible term) at the very surface. They handle vision, feeling, route planning, and abstract concepts such as containment. A logical choice is like walking through a forest avoiding trees. Sets can be handled both ways. Most process them as containment, but how do you deal with sets that have themselves as subsets? Use motor programs as directed edges in a graph from set to element and put a cycle. This is why diagrams work differently. I like brains. Maybe I am a zombie. I am Dead Man, after all.
why do you have pointless buzzing sound in background? Its so annoying
The question of adding music to my videos is always something I wrestle with after editing them. I like the idea of no music, but then the video sounds almost empty without it. For this video, I was trying to go for an ambient type of sound that would be faint in the background and not that noticeable, which I guess I failed on. Your critique has been noted. I'll keep that in mind for the future. Thank you.
Ah. Ok. This is why Im so unpopular.
New favourite channel. Youre on a wavelength, keep it up.
You have two arms, add two more and you have forearms... or another person standing next to you, but now you have four forearms or put simply, twenty fingers.
You can prove “p or not p” via reductio: take some already proven true proposition x. Assume “not (p or not p)” for the undecidable p. Get “(p and not p)” from your assumption. Use this contradiction to derive
If a fact only "becomes true" when it is proven, them your not talking about reality. You're talking about something else.
"Our experience of time" is an attempt to make it sound derivative, as if time doesn't exist.
What does it mean for time to exist though? It's "what clocks measure" but beyond that, we don't know what it is at all. We can't even experience it directly, we only ever infer it.
Time is emergent, it doesn't exist on its own
@@manso306 we experience time ALL THE TIME. Why do you think you weight your sentences with the words in a specific order? Try reading your sentences in a random order of words. Does it still have the same meaning? Time is that some things can be considered "before" and others "after". We have continuous visceral experience of time, but you've apparently disconnected part of your mind, which is possible.
@@MadolynGabriel do you mean it doesn't exist outside the universe? It doesn't need to. That's a false requirement. Nothing real exists outside the universe.
@@TreeLuvBurdpuwhat you're describing is (obviously) inferring time from thoughts that happen
Math is constructed from reality. So, yes.
You really don't know about that, although it's feasible that math is embedded into reality as the possibilities of configurations of the neuronal system in our brain, it might be the opposite and reality which is built upon math and just our brain which can decrypt the conceptual world using neuronal system. It's really not provable and not that important, but there certainly seem to be a possibility that the conceptual world is not built upon the real world but encrypted into to it and such that real entities like brain can partially decrypt that.
@ethanjahan780 when you say "you really don't know about that", you're saying what I know might not correspond with reality, right? Because we have the same test in math, and that is how math was developed.
@TreeLuvBurdpu, I'm sorry I don't understand what you mean in your comment.
@@ethanjahan780 there was an autocorrect wrong word.
Donald Duck in "Mathmagic Land" was the first thing that came to mind.
autopoesis
Interesting. Sounds like David Hume set to math.
At 5:36 intuitionistic logic (IL) is defined as requiring a demonstration of the inability to construct something as proof of its opposite (assumedly, this says that proving P requires direct construction of P rather than simply an inability to construct its opposite), and classical logic (CL) is defined as proving P by an inability to construct its opposite ( ¬P). It sounds like IL and CL are actually indistinguishable since you could always substitute q= ¬P as a workaround. Maybe this isn't a complete definition?
It basically amounts to a rejection of ~~P => P, which is classically valid but not intuitionistically. You can assume sqrt 2 is a rational number and conclude an absurdity intuitionistically, and derive the statement "sqrt 2 is not rational" That statement however doesn't tell you how to actually construct the square root of 2 as an irrational number
Mathematics doesn't use logic. It's a made up language
Mathematics is the science of problem solving. I don't see where you are going with this. You seem to be limiting the type of problems that can be addressed.
That's right, excluding the law of excluded middle is just limiting tools for truth. But there is still a nice will under that, to construct explicitly mathematical concepts, which can be cool.
It is truly remarkable and uncanny how applicable math continues to be toward describing and predicting reality. That is my one hangup about believing fictional-mathematics is true. It's as if the fictional idea of isometry sprang out of the story we created, infecting our world with structure, order, and multiplicity the same way that mathematics uses structure, order, and multiplicity. Plus, one must consider that our conception of "2" isn't any less concrete than our conception of "tree" or "sun". A pair of apples has "2ness" just as much as it has "appleness" because both depend on a conceiver and categorizer to arrive at both descriptions. (And that pair of apples simultaneously lacks "2ness" from other conceptions and categories, such as from an atomic perspective or the bushel perspective).
It would seem like we can deconstruct intuitionism into 2 distinct independent concepts : -Rejecting excluded middle. -Rejecting existence of the conceptual world. The two are really independent, I don't know why they are packed together.
Conceptual? I read it as a rejection of objective criteria for what number goes where. But to be fair, the whole point and protest of this philosophy is rather abstruce, honestly; what is even the insight?
I like the word abstruse, I would go further into risky words and say that it's essentially irrelevant. Even though constructive mathematics is nice, preventing one from usage of excluded middle is just excluding free tools for truth. Furthermore, Rejecting existence of the conceptual world and saying that it is embedded into real material world really is irrelevant to one's experience of mathematics and lies more into the category of "fun thoughts without any consequences".
Intuitionists don't reject the existence of the conceptual world, they just reject that it exists outside of our minds.
@antoniusnies-komponistpian2172, what you're saying is what I mean by rejecting existence of the conceptual world. What would be accepting it is to postulate existence of another world (of concepts) which would exist independently of the real world and our minds (it would not be located anywhere in the real world tho). But the thing is that either ways you experience thinking in the same way and neither one of the options is provable in any way. So as I was saying, it might be fun to think sometimes about it, but it doesn't really lead anywhere.
@@ethanjahan780 Why aren't minds part of the real world?
What a limiting point of view…. [I’m as much in favour of constructivist mathematics as anyone else, because I want to actually know the answer… But mathematical progress would be greatly slowed if one insisted on this, or many of the other intuitionist self-imposed restrictions.]
There is a common misconception in this video when talking about proof by contradiction in the chapter „Proof of Negation vs Proof by Contradiction“. The basic structure of proofs of propositions like ¬P are the same in classical and intuitionistic logic. In both systems you will assume P and derive absurdity from it. The difference lies in proofing P. In intuitionistical logic you can't instead just proof ¬¬P like you can in classical logic.
Question: is it the case in classical logic that P and ¬P are the only options in whatsoever first order logical proposal one makes? Because I find that methodological presumption to be worthy of critique. It presumes that the minds of the interloqutors making the propositions have sufficiently grasped the nature of the subject/continuum they are discussing so as to be _absolutely_ certain that P is a meaningful and valid proposition in the first place. Real logic, i.e. the praxis of the theory, is vulnerable to human error.
@@john-paulgies4313 I'm not sure what exactly you are talking about. But I think that your assertion isn't really discussed by mathematicians (but may be discussed by philosophers). In mathematics we don't really think about propositions as sentences like „The weather is good“ which would be very subjective and ambigious. Instead we only think about perfectly constructed propositions, like ∃x:(∀n∈ℕ:x=2·n}). Those statements are by the nature of their construction well constructed.
He's a constructivist, lol...
Also there is no way to create a natural direction or progression from numbers 1,2,3 etc. They are just symbols. We use them in the sequence because it was hammerd into us in school. We can extend the sequence in the same spirit and feel like something increases, but that's absolutely not given. It can be time, length, a dimension. There is no saying for this dimension there are positive, negative, rational irrational or complex numbers. So you have to start with measuring and can then postulate numbers..
Its not intiutionist but realist. Mathemantics is a simulation language and some of its numbers can only be generated using algorithms. If you want to state fact you can not assume algorithmic steps have been performed that have not been performed. The beauty of this view is that it aligns perfectly with engineering and physics. It basically tells maths to realize its not a realm of its own, its just a simulation language for reality. Sure you can count the colors of racehorces and do statistics, that has nothing to do with the race or its outcome. Likewise there's many things you can say about maths that are practically irrelevant.
Interesting video but please don't use this background sound. It's OK with small laptop speakers but it's really annoying with systems that have a subwoofer!
Noted. I'll keep that in mind for the future. Thank you.
Basically Buddhism.
What else could it be? Is a creation, as every piece or art is.
I have no clue if I'm stupid or if this is stupid
It is stupid. We are teaching in middle school where math comes from, most people are just not paying enough attention.
Where does it come from?
@blausgschpangschtvohindere2210 Primitive physical observations of nature.
Could be both (no offense; I don't know you). All I can speak to is that the idea seems to be an underdeveloped critique of abstraction motivated by a poor understanding of its right relationship with the external world.
@@lepidoptera9337Is this a contradiction to Intuitionism?
Basic Buddhism
Do you think these povs (dharmic povs) have within them the ability to shift the pov of the mathematical pov to solve problems within it?
explain what this has to do with buddhism, with references in the pali canon
Great video. At times I saw parallels to ''Wolfram's Physics'' and him wanting to replace math with computation there. He has this concept of computational irreducablity. The idea basically says as time marches on, it creates and updates the universe, inclusively the observer, who is a part of it, and for most things there are no mathematical shortcuts to know the future state of the universe. Therefor you also can't compute it faster than the universe computes it via it's update-function, since your state updates only as fast as the universe does. So now I am thinking about, how these two ideas, Intuitionalism in math and this physics hypothesis maybe complement each other, because it would be like the universe would be creating new mathematics through its computationally irreducable process that includes that observer doing the math 🤔 ... It's maybe a bit far-fetched.😊 (edit: I mean philosophically Wolfram's Physics, doesn't satisfy me ... but from as a different view on physics its interesting )
Wow, sounds interesting
Yes, Wolfram is a guy who has a hammer and sees the world as consisting of nails.
Man confuses basic fact that math needs time to make (like everything else) with idea that time makes math lol you’ll love the ‘time causes gravity’ theory too 😂
"Time causes gravity" is clearly retarded. Obviously, it's the fourth dimension which causes time 🙄 duh, people
My ex👩🎓 was an intuitionist. It is not a science. I decided to divorce, because her intuitionism👩💻 was unbearable.
You’re kidding, surely?
If you did nothing that contributed to the divorce, then good for you 🙂↕️
That doesn't seem like an insurmountable obstacle to the married life. Did she make certain demands of your relationship that were violent against your common life based on this philosophy? Like, insisting that lying to you is okay because intuitionism proves it?
That's pretty funny😂
good choice, man.
This mental location of numbers would imply each of us has a separate number 2 in his/her head. Which seems absurd, considering we use "2" the same way and it is the shared use which reflects the meaning.
Read about the psychological relativity of color. We can't prove I see the same "red" in my head as you, but we can agree a given color is "red", not by some intrinsic "redness" but by the relations it establishes with other colours and its surroundings. Just like in cathegory theory numbers aren't derived from prior elements but from the structure of morphisms between them (think of the different properties of "2" in Z, Z3 or R)
@@alicwz5515 That's just what the "redness" of red is; that's what the "twoness" of 2 is: we see the same red and know the same 2 because our qualitative perception of red, our quantitative understanding of 2, is convergent, coherent, univocal.
@alicwz5515 intrinsic redness can be found in viewing light in the 620 - 750 nanometer range of wavelengths
Imagine the location of "2" as a meal people make from a list of ingredients. No 2 people's meals will be exactly the same due to different utensils, slightly different amounts of ingredients, and random mixing. Everyone might agree that you brought a lasagna to the potluck and agree that it should be served with green beans, but it's impossible to have brought the "same" lasagna as someone else. I do think that "the real numbers" also has a location, and claiming they only exist as a process is just denying the existence of a real concept.
this is really good and thought provoking, thankyou for making it
Thank you
Traveler, there is no path, the path is made by walking. --Antonio Machado (Spanish Poet) Time doesn't exist, what does exist is the perpetual unfolding and evolution of the universe. There is only NOW.
If you're asking where the fundamental axioms of mathematics come from, at least we should be able to agree that deductive reasoning from axioms will not suffice! This method of deducting certainties fails with axioms. If we're not to solve this problem, perhaps we could try to resolve it, instead. This is not a mathematical question, this is the science of mathematics. Time has something to do with it, as does energy, and physics. As does psychology and neuroscience, as what good's an unintelligible axiom? As does sociology, and economics, as what good is an axiom that only one person uses? The very process of coming up with axioms is based on doing instead of knowing. It's these huge gaps in knowledge about our doings that require scientific resolution, instead of solution.
Sure, inventing an axiom is a process, but saying that the implications of that axiom are meaningless unless a certain number of people understand it and have practical use for it is strange to me. For instance, once the rules of chess are defined, it becomes a deductive certainty that you can checkmate with 2 bishops and a king.
ye if this was true we wouldn’t be talking about Gilbert but this burger mf or whatever his name is, this so called theory is not even wrong it’s just some hypothetical bs that doesn’t help to advance math
lol 😂 We’re talking about Hilbert not Gilbert or Dilbert!
@@MikeWiest for all i care i can call him retarbert lol but actually in my mother's tongue his name is slept with a g at the start so yeah it's actually just an gonest mistake at my part
Is Dumbness a product of our perception of Christopher Langan?