
- 53
- 811 920
Mulkek
Kuwait
Приєднався 8 сер 2018
Welcome to the Mulkek channel, where I explore and simplify mathematics using different ways to make it interesting! My videos are designed to help students at both high school and college levels with courses in algebra, geometry, precalculus, and calculus. I completed my Master’s in Applied Mathematics and PhD in Analysis and Computational Mathematics in Edinburgh, one of the most beautiful cities in the world.
I believe that loving math is the key to making life easier and more fun!
I deeply APPRECIATE EVERY SINGLE SUBSCRIBER, LIKE, COMMENT, AND VIEW. The love and support I get from you are sometimes overwhelming.
Hit SUBSCRIBE to catch my NEW videos first and JOIN me on this exciting mathematical journey.
I believe that loving math is the key to making life easier and more fun!
I deeply APPRECIATE EVERY SINGLE SUBSCRIBER, LIKE, COMMENT, AND VIEW. The love and support I get from you are sometimes overwhelming.
Hit SUBSCRIBE to catch my NEW videos first and JOIN me on this exciting mathematical journey.
a^2-b^2 - Algebraic proof of a square minus b square
❖ Algebraic proof of a square minus b square which is a^2-b^2=(a+b)(a-b)
In this video, we provide a step-by-step algebraic proof of the difference of two squares formula:
a^2-b^2=(a+b)(a-b)
❖ a^2-b^2, which it called difference of two squares.
The link to Math Fun playlist:
ua-cam.com/play/PLPm9fyDNbwj-5bYL18GftxfvOipvmK49h.html
The link to Geometry playlist:
ua-cam.com/play/PLPm9fyDNbwj-uRAABjUUaw_TYEGwGVNWF.html&si=bsZWFp7nQhKqYGMd
The link to the Linear Algebra playlist:
ua-cam.com/play/PLPm9fyDNbwj9zUIHKYfNwkfeWWBamk-q_.html
My Website:
www.mulkek.com
Subscribe to My Channel to check out for more videos:
ua-cam.com/users/Mulkek
In this video, we provide a step-by-step algebraic proof of the difference of two squares formula:
a^2-b^2=(a+b)(a-b)
❖ a^2-b^2, which it called difference of two squares.
The link to Math Fun playlist:
ua-cam.com/play/PLPm9fyDNbwj-5bYL18GftxfvOipvmK49h.html
The link to Geometry playlist:
ua-cam.com/play/PLPm9fyDNbwj-uRAABjUUaw_TYEGwGVNWF.html&si=bsZWFp7nQhKqYGMd
The link to the Linear Algebra playlist:
ua-cam.com/play/PLPm9fyDNbwj9zUIHKYfNwkfeWWBamk-q_.html
My Website:
www.mulkek.com
Subscribe to My Channel to check out for more videos:
ua-cam.com/users/Mulkek
Переглядів: 385
Відео
a^2-b^2 - Geometrical Explanation and Derivation of a square minus b square
Переглядів 3523 місяці тому
Geometrical Explanation and Derivation of a square minus b square which is a^2-b^2=(a b)(a-b) � a^2-b^2, which it called difference of two squares. � Visualize a^2-b^2=(a b)(a-b) geometrically! � The area of a square is the product of the two sides of the square. Area of square = side x side. � The area of a rectangle can be calculated by multiplying the lengths of two adjacent sides, Area of recta...
Matrix inverse & transpose examples
Переглядів 3903 місяці тому
❖In this video, we explore Matrix inverse & transpose examples, showing how these concepts are applied in linear algebra. *Example 1* Let A=[1 2;1 3] and B=[1 -1 2;3 2 0]. a) Find if possible, A^2 - (2A)^T. b) Find C if (B^T C)A^(-1) = B^T. *Example 2* Let A=[2 -2 -1;3 -1 1] and B=[1 0;1 -4;2 -5]. Find a matrix C such that CA=B^T. *Verification for Example 2* To ensure the correctness of the so...
Matrix Transpose and its Properties
Переглядів 3584 місяці тому
� In this video, we have explored the Matrix Transpose and its Properties. Dive into the foundations of Matrix Transposition, a critical operation in Linear Algebra. Learn about the specific properties that define Transposition through clear explanations and see these principles applied in a practical example. *Matrix Transpose and Its Properties with Examples:* 1. Transpose of identity and zero...
Matrix inverse and its properties
Переглядів 6216 місяців тому
� In this video, we have explored the Matrix inverse and its properties. Discover what makes the matrix inverse a unique and powerful tool in linear algebra. Learn through a series of explained properties and see these theories in action through a practical example involving matrix equations. *Matrix inverse and its properties with Examples:* 1. A^{-1} is unique. 2. Reversing an inverse brings y...
Using Matrix inverse to solve two Linear Systems
Переглядів 5708 місяців тому
� Using Matrix inverse to solve two Linear Systems. We are using Matrix inverse to solve two Linear Systems. First: You need to write an Augmented Matrix containing the original Matrix and the Identity Matrix, Then: You need to convert the original Matrix into the Identity Matrix using Elementary Row Operations (Apply Reduced Row Echelon Form (RREF) for the left side of the Augmented Matrix). Th...
Solving two Linear Systems using the inverse
Переглядів 73111 місяців тому
� In this video, we are solving Two Linear Systems Ax=b and Ax=c using the inverse. � To find the inverse of a Matrix, we have mentioned two ways to answer. Then, we used the inverse of a Matrix to solve Two Linear Systems. � Question 1, we have solved it in two methods: The first method: You need to write an Augmented Matrix containing the original Matrix and the Identity Matrix, Then, You need t...
Find the inverse of a Matrix and solve a Linear System Ax=b
Переглядів 1,3 тис.Рік тому
� In this video, we have explained how to find the inverse of a Matrix and solve a Linear System � To find the inverse of a Matrix, we have mentioned two ways to answer. Then, we used the inverse of a Matrix to solve a Linear System. � Question 1, we have solved it in two methods: The first method: You need to write an Augmented Matrix containing the original Matrix and the Identity Matrix (which ...
Inverse of a Matrix
Переглядів 2,2 тис.Рік тому
� In this video, we have explained how to solve a linear system using the inverse of a matrix, which is a precalculus video tutorial. This video builds on our previous tutorials where we demonstrated how to find the inverse of 2x2, 3x3, and 4x4 matrices. � To find the inverse of a matrix, you need to create an augmented matrix containing the original matrix and the identity matrix (which has the ...
Inverse of a 4x4 Matrix
Переглядів 37 тис.Рік тому
� In this video, we have explained how to find the inverse of a 4x4 matrix, which is a precalculus video tutorial. The previous videos showed how to find the inverse of a 2x2 and a 3x3 matrix. � To find the inverse of a 4x4 matrix, you need to write an augmented matrix containing the original matrix and the identity matrix (which has the same size as the original matrix), Then, You need to conver...
Inverse of a 3x3 Matrix
Переглядів 3,2 тис.2 роки тому
� In this video, we have explained how to compute the inverse of a 3x3 matrix, which is a precalculus video tutorial. The previous videos showed how to find the inverse of a 2x2 matrix. � To find the inverse of a 3x3 matrix, you need to write an augmented matrix containing the original matrix and the identity matrix (which has the same size as the original matrix), Then, You need to convert the o...
Inverse of a 2x2 Matrix
Переглядів 1,3 тис.2 роки тому
� In this video, we have explained how to find the inverse of a 2x2 matrix, which is a precalculus video tutorial. � To find the inverse of a 2x2 matrix, we have mentioned two ways to answer. � The first way to answer (The first method): You need to write an augmented matrix containing the original matrix and the identity matrix (which has the same size as the original matrix), Then, You need to c...
Negative powers of a matrix
Переглядів 4,2 тис.3 роки тому
� In the video, we learn about the negative powers of a matrix. � The tutorial starts by calculating A^(-1), A^(-2), and A^(-3), then moves on to formulating a general formula for A^n where n is any negative integer. By using this formula, we compute A^(-2025) � The negative power A^n of a matrix A, where n is a negative integer is defined as the matrix product of n copies of the inverse of A To f...
Powers of a matrix
Переглядів 28 тис.3 роки тому
� In the lesson, we have explained the Powers of a matrix. � The power A^n of a matrix A for n a nonnegative integer n is defined as the matrix product of n copies of A, where A is a square matrix (for example the size of A can be 2x2, 3x3, and so on). A^0 is defined to be the identity matrix of the same size, where A^0=I_n ( I_n is nxn an identity matrix with the same size as A). � The number of ...
Gauss Jordan Elimination & Reduced Row Echelon Form | RREF
Переглядів 7 тис.3 роки тому
� To solve a linear system of equations by Gauss Jordan elimination, we have to put the augmented matrix in Reduced Row Echelon Form which is called RREF. � This Linear Algebra video tutorial provides a basic introduction to the Gauss-Jordan elimination which is a process that involves elementary row operations with 3x3 matrices which allows you to solve a system of linear equations with 3 variab...
Gaussian Elimination & Row Echelon Form | REF
Переглядів 16 тис.3 роки тому
Gaussian Elimination & Row Echelon Form | REF
How to multiply matrices in Python (Spyder IDE)
Переглядів 2 тис.3 роки тому
How to multiply matrices in Python (Spyder IDE)
(a-b)^2 - Geometrical Explanation and Derivation of a minus b whole square
Переглядів 4,2 тис.3 роки тому
(a-b)^2 - Geometrical Explanation and Derivation of a minus b whole square
(a+b)^2 - Geometrical Explanation and Derivation of a plus b whole square
Переглядів 8383 роки тому
(a b)^2 - Geometrical Explanation and Derivation of a plus b whole square
How Multiply Matrices? Find all values of k, if any, that satisfy the equation
Переглядів 6 тис.3 роки тому
How Multiply Matrices? Find all values of k, if any, that satisfy the equation
Determine if Equations are Linear or Nonlinear
Переглядів 8 тис.4 роки тому
Determine if Equations are Linear or Nonlinear
Find the values of k which give, one Solution, no Solution, or infinitely Many Solutions
Переглядів 39 тис.4 роки тому
Find the values of k which give, one Solution, no Solution, or infinitely Many Solutions
Determine which values of k will give, one Solution, no Solution, or infinitely Many Solutions
Переглядів 135 тис.4 роки тому
Determine which values of k will give, one Solution, no Solution, or infinitely Many Solutions
Connection between row equivalence & the inverse
Переглядів 3,3 тис.4 роки тому
Connection between row equivalence & the inverse
Example of row equivalence & elementary row operations
Переглядів 51 тис.4 роки тому
Example of row equivalence & elementary row operations
Solving three linear systems Ax=b with same coefficients
Переглядів 1,2 тис.4 роки тому
Solving three linear systems Ax=b with same coefficients


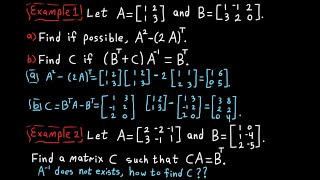






You literally saved me😭😭
On those last two equations to form the identity matrix the one below is supposed to equate to R2 not R1 3:42
Thanks, I'm watching it in 2024 and trust me it made the whole stuff so simple
what if the second and third rows are all 0? does it include having infinite solutions?
If the second and third rows are all 0s, yes, it usually means there are infinitely many solutions. This happens because there aren’t enough equations to find all the variables (x_2 and x_3).
THE VOICE FILTER... OUCH
Thank you..
You're so welcome! 😇
You're just amazing💖💖
Thank you so much! I’m really glad you enjoyed the video 😇
Nice! Amazing! Fantastic!
Thank you so much! I’m thrilled you enjoyed the video! 😊
I think that it is not neccesarry to perform R1-2R2 -> R1 . Is I am right ? If wrong then correct me . Please
You're absolutely right! It's not necessary to perform R_1-2R_2 ---> R_1 if you observe that applying R_3 + 2R_2 -> R_3 leads to [0 0 0 0|1] ], which indicates no solution. Great observation! 👍
you saved me you have no idea
I’m so glad to hear it helped! Thanks for watching & good luck with your studies 😇
idk why this has so low views. pretty good at explaning easily
Thank you so much! I’m glad you found the explanation easy to follow. Hopefully, more people will find it helpful over time! 😇
Thanks
Glad you liked it 😇
we need to do row echelon form or reduced?
For this problem, you can use row echelon form to determine the type of solution. Reduced row echelon form is also an option, but it’s not necessary unless you want further simplification. Good luck, and feel free to ask if you have any more questions 👍
Habibi very good teacher mashallah
Thank you so much & Glad you liked it
Augustine Canyon
Thanks a lot, but please tell me how to solve the equation a^2-5. I couldn't find a solution.
Thank you for your comment! Just to clarify, did you mean k^2−4 instead of a^2-5? Let me know, and I'd be happy to help 😇
Tysm. The book decided to not explain this but still put excersises about this topic. I also have a test tomorrow so you're an absolute life saver👍
You're very welcome! I’m glad the video was helpful. If you’re interested in more practice, feel free to check out my other video on a similar topic: "Find the values of k which give one Solution, no Solution, or infinitely Many Solutions", and here is the video link: ua-cam.com/video/61vt1nDHOKo/v-deo.htmlsi=3Dt2q1Q91RAzlJeq I'm planning to create more videos like this in the future, so stay tuned! 😇
Amazing explanation thanks a bunch!!! ❣
Thank you so much! I’m so glad you enjoyed the explanation 😇
my goat
Thank you so much & I’m so glad you found the video Greatest of All Time 😇
Imagine this guy is better than my prof in uni
Thank you so much! I’m really glad you found the video helpful 😇
thankyou this helps me alot
You're so welcome & I’m really glad you found the video helpful 😇
thank you so much ! great video
Glad you enjoyed it!
The most underrated content to ever be 😊
Thank you so much for your encouraging words! I’m thrilled to hear you enjoyed the content. Your support is incredibly valuable to me 😇
@@Mulkek you are welcome, I look forward to watching your upcoming videos, I can't wait 😄😂😄
Thanks bro
Thanks for watching, and I'm glad you liked it 😇
Thanks
You're so welcome
Wow! This is the most enriching statistics lesson I've ever had. You tackled matrices perfectly. Thank you! I'm your new follower.
I’m so glad you found the video enriching. Your support inspires me to continue creating content that makes a difference. Thank you so much for your kind words & for following 😇
Please upload a video on (a+b) (a-b) =a square - b square on a geometical shape???
Thank you for your suggestion! I will definitely make a video on the Geometric Explanation and Derivation of a² - b² = (a+b)(a-b) very soon. It will be the next upload, so hit SUBSCRIBE to catch it first! Stay tuned 😇
Nice lecture Software name plzz
thank you so muchh i neeedded dat
So glad it helped you! Thanks for watching 😇
👍🏽
Glad you liked 😇
Ofcourse the video was awesome and ofcourse it was very helpful
Thank you so much & I'm thrilled to hear that you found the video awesome and helpful 😇
thanks it was that simple
Glad to hear you found it simple & Thanks for watching 😇
What level is this for gcse?
Thanks for your question! This video covers topics from Linear Algebra that are typically taught at the College or University Level, so it's more Advanced than GCSE. However, in some countries, the introduction to matrices, including operations like Addition, Subtraction, Multiplication, and Solving Systems like Two Equations with Two Variables, is part of the High School Mathematics Curriculum. If you're looking to understand the basics of Matrix Operations, you might find my other videos in the *Linear Algebra playlist* helpful. These include *Scalar Multiplication of Matrices* ua-cam.com/video/SK1jBwFh4t4/v-deo.htmlsi=Cf2mOTFBGfjMCldD *Adding and Subtracting Matrices* ua-cam.com/video/4WS9xCU07C0/v-deo.htmlsi=HTVnlWn15xefi66X *Multiplying Matrices* ua-cam.com/video/-_1QKxx_sus/v-deo.htmlsi=CrVenkYrVb1aob0i *Solving Two Linear Systems Using the Inverse* ua-cam.com/video/ZOFOx3g8Oq0/v-deo.htmlsi=DsoG0HgBsqfgELaA *Linear Algebra Playlist* ua-cam.com/play/PLPm9fyDNbwj9zUIHKYfNwkfeWWBamk-q_.html These topics might provide a good foundation and are definitely worth checking out if you're interested in Foundational Mathematics. Let me know if you have any other questions 😇
thank you teacher
You are so welcome 😇
You simplified this in just 20 mins😮. I didn't understand it in our 3-hour lecture at school, and now I fully understand.
Wow, that’s fantastic to hear😇! I’m so glad the video helped clarify things for you. It’s amazing what we can sometimes accomplish in just a short time with the right approach. Keep up the great work, and if you have any more questions as you continue to explore mathematics, feel free to ask. Thanks for watching and sharing your success with me! 😊
Your video are wonderful
Really good explanation!Hoping for more videos
Thank you so much for your kind words! I'm glad you found the explanation helpful. Stay tuned, more videos are on the way soon😊
im guessing this is why we don't do inverse of a 4x4 at A-level, inverse of a 3x3 without a calculator takes enough time by itself
You're absolutely right, calculating the inverse of a 4x4 matrix by hand can be quite time-consuming and complex, which is why it's often not covered at A-level without the aid of technology. It's great for deepening your understanding of matrix operations, though! If you ever decide to tackle it, patience and practice are key. Thanks for watching and sharing your thoughts 😇
Very nice, thanks.
Most welcome
Thank you
Thank you for watching 😇
Thank you. ❤
Thank you for watching 😇
I've been here b4; the video was already liked. Now i'm back with a new course where i need to relearn this XD
Welcome back! I'm glad to hear that you find the video helpful for your new course as well. It’s always good to revisit and reinforce these concepts. Best of luck with your studies, and if you have any questions, feel free to ask & thanks for watching again 😇
Wow well understood
I'm happy to hear that & glad you found it helpful 😇
Thankyou so much buddy 🫡
You're welcome! I'm glad you found the video helpful. Thanks for watching & for your kind words! 😊
Can't we just directly prove R1 = 2(R1) R2 = R2 + R1 And by doing tgis with A matrix we can derive B... I mean this will save a lot of time Will that be considered right?
If you do R2 = R2 + R1 for matrix A, the second row will become [4, 6], which is not equal to the second row in matrix B: [5, 8]. So, this way is not sufficient to show that matrices A and B are row equivalent. Let me know if you have any more questions or need further clarification; feel free to ask & good luck with your studies 😇
Legend 💯
Thank you so much! I’m really glad you enjoyed the video. Your support means a lot! 😇
Thank you
You're so welcome
amazing summary ,please make one of trigonometry<3 ;-;
Thank you for the great feedback! I'm thrilled you enjoyed the video and appreciate your suggestion for a trigonometry video. It’s a fantastic idea, and I'm definitely considering creating a similar summary for trigonometry concepts. Stay tuned, and good luck with your studies! 😇
thanks alot!!! :)
You're so welcome😇
Gracefully acknowledged!!! I am the first one to comment!!
Thanks for being the first to comment! Really appreciate it 😇
sir can you help me with a certain question
Of course, I'd be happy to help! Please share your question here, and I'll do my best to provide a clear explanation. Additionally, I'll consider addressing these types of questions in more detail in future videos. Looking forward to assisting you!