Відео

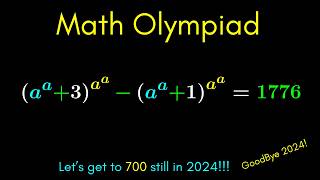
Very bad solution. It's easy to see a series of substitutions (1+x) = t, then y=1/t, then u=2y-1, which in 3 lines leads us to biquadratic u^4 + 6u^2 +1 = 8*13/14 Last substitution is because one can see that f(y) = f(1-y), therefore y=(u+1)/2 and y-1 = (u-1)/2

Try leaving a question at the end of the video so that we can attempt it and then solve it in the next. Also, expand the questions to include other topics calculus and geometry, etc, rather than these types of problems only. 🎉

Almost identical to one of your previous problems. If the right side = n/(n+1), let m = √(4n +1) then the solutions are (m - 1)/(m +1) and (m + 1)/(m - 1). So for n = 72, m = 17 and the solutions are 16/18 and 18/16 or 8/9 and 9/8.

Or substitute u = x + 1/x The equation reduces to (u + 1)/(u² -1) = 1/(u - 1) = 6/7 or u = 13/6 x = 2/3 or 3/2

Or let u = (10 + 3√11) and v = (10 + 3√11) uˣ + vˣ = 398 uv = 1 and v = 1/u uˣ + 1/uˣ = 398 u²ˣ - 398uˣ + 1 = 0 Let w = uˣ w² - 398w + 1 = 0 w = 199 ± 60√11 w = (10 + 3√11)² or (10 + 3√11)⁻² w = uˣ = (10 + 3√11)ˣ = (10 + 3√11)² or (10 + 3√11)⁻² x = ±2

Amazing!

That ±2 is magical hhahhaha

Nice content 🎉 Pls continue with this type of work until your channel explodes ❤ Keep it up

Nice bro 👍

Good luck with your channel. You're going to need it.

I'm happy to be among the first 1000 subscribers of this channel 🎉

Cool Math Problem. Thanks a lot.

Nice

?!?

I prefer the author’s solution

Great❤

The solution has some fundamental mistakes as by default definition of ln function has positive real domain. So this solution is not correct.

Ridiculous!

If you took x^2022 common (x+1+1/x)/(x²+1+1/x²)=6/7 u+1/u²-1=6/7 u-1=7/6 u=13/6 x+1/x=13/6 A bit quicker

By knowing this 3^3+4^3=91=6^3-5^3, problem is easily defined

LOL, take a look once again beginning and the end. " Simplify" 😅

what's simplified about it?

Sorry but how do you know that you can take the ln of -π , isn't in the domain ?or you can do it.Why can a negative number raised by a positive number be positive?

What abt x_3 to x_2023

Cool solution, but your handwriting could use some work.

if a=4 ,4^4=256>91 therefore a<4, if a=2, 2^2+3^2=4+9=13, therefore a>2, the only possible answer is a=3

Notice that the roots we found, x₁ = 2/3 and x₂ = 3/2, are reciprocals of each other. This is not accidental. How could we have predicted this?

My thinking is that √x+√(-x) = √x ± i√x = (1±i)√x => √x = 10/(1±i). No substitutions here, just brute forcing it.

I think its easier to square both size of the equation

The writing is hard to understand.

By inspection I would say that x=50i, so x and -x lie on opposite sides of a circle centered on the origin of the complex plane. Then √x=(5√2)(√2/2)(1+i) and √(-x)=(5√2)(√2/2)(1-i) and √x+√(-x)=(5√2)(√2/2)+(5√2)(√2/2)=10.

p=π^sen²x p²+π=p(π+1) p²-p(π+1)+π=0 (p-π)(p-1)=0 π^sen²x=π π^sen²x=1 sen²x=1 sen²x=0 senx=1 senx=-1 senx=0 x=πn/2, n is natural

Wrong solution. Strictly speaking, (a) is not a natural number. One can guess a=3 (as I did) and further proof that it is the only solution because of the function is monotonic for, say, a>2.

Let y= 7^x, giving the cubic y + y^2 + y^3 = 14. By inspection, y = 2 is one solution. Therefore, (y - 2) is one factor of the cubic. Divide the cubic by (y - 2) to find the other, quadratic factor, which can be solved using the quadratic formula. Now knowing the values of 7^x, you can find x by applying the logarithm function.

You rewrote a lot of material by mouse that could have been copied and pasted.

That is a pretty nice algebra problem.

Why is my message hidden?

by inspection on the thumbnail, just casually note that 3⁴-4³=17

You can differentiate to find the function in the LHS is strictly increasing for a>=2. Thus, the equation cannot have more than one solution, and a=3 works, so it must be the only one.

you can use the Newton binomial to factorize this and get to a being a divisor of 18, so a=2 or 3 or 9. Then it is straightforward.

I guess you just try 3 is the fastest methods

Great problem, but ugly writing... Please take a calligraphy course. For π, you can write it with 3 straight lines. Also, see your keyboard, the digit 1 is write with 2 straight lines, one vertical and one oblique, 1 ≠ I. And, lowercase x is handwrote as curved 𝑥, not straight uppercase X. For the solving: as cos² 𝑥 = 1 - sin² 𝑥, if you set X to π^(sin² 𝑥), the equation becomes X + π/X= π + 1 (note that I use uppercase X). As π^(sin² 𝑥) is never 0, X is never 0 and then the equation becomes X² + π = X(π + 1). This quadratic equation has 2 solutions: X = π or X = 1 (the discriminant is (π - 1)², so it is greater than 0). So π^(sin² 𝑥) = π or π^(sin² 𝑥) =1, so sin² 𝑥 = 1 or sin² 𝑥 = 0. For sin² 𝑥 = 1, 𝑥 = π/2 + kπ, with k ∈ ℤ. For sin² 𝑥 = 0, 𝑥 = kπ, with k ∈ ℤ. Conclusion: 𝑥 = kπ/2, with k ∈ ℤ.

since a an integer, reducing mod a gives 17=-1 (mod a) so a is a factor of 18. reducing mod a+1 we get (-1)^a+1=17 mod a+1 so a+1 is either an odd factor of 18 or an even factor of 16 writing down the values 18:1,2,6,3,9 16:2,4,8,16 so a=1,2,3 is the only possibilities and we can check by hand 1,2 isnt and 3 is a solution

You can write all the solutions you found as “x = kpi/2”

you assumed that a^((a+1)/2)+(a+1)^(a/2) is an integer (knowing that a is a positive integer). This assumption is generally wrong and accidentally works for this specific case

Is this really imo problem?

Thanks Mr, but you missed this solution : x_3 = kπ , k€Z where sinx=0

NIce resolution!

Nice question keep going

very intersting, few sugessting increase your audio,