
- 111
- 1 146 098
Arneauxtje
Приєднався 14 жов 2011
Visualizations of (hyper)complex dynamical systems, most of them otherwise known as Fractals.
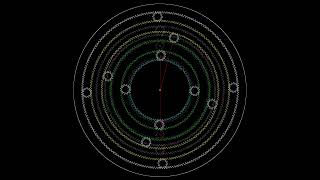
And yet another planetary gear clock, last one, I promise
Can't believe I didn't think of this setup before; this must be one of the most straightforward and compact drivetrain arrangements for displaying seconds, minutes and hours.
Technically it's not a full-fledged planetary gear since the satellite wheels only run on a planet wheel while not simultaneously on an outer ring wheel, but who cares.
Technically it's not a full-fledged planetary gear since the satellite wheels only run on a planet wheel while not simultaneously on an outer ring wheel, but who cares.
Переглядів: 1 102
Відео
Yet still another planetary gear clock design
Переглядів 1945 місяців тому
This one's rather sneaky. The planet wheels run on a twin set of satellite wheels with a small difference in gear teeth number, but on the same pitch circle, by tweaking the gear module a bit. The static wheel has less teeth than the moving one, and as a result the latter one turns clockwise.
Yet another planetary gear clock design
Переглядів 3156 місяців тому
I consider this to be an improvement on a design made years ago, where the satellite wheels are driven from a center stack of gears. In this case, the yellow satellite wheel drives the green and cyan ones, which makes for a more efficient set-up. As per the previous design, the planetary gears tell the time. The whole assembly can be actuated at the center wheel or any of the two satellite whee...
Another planetary gear clock design
Переглядів 2577 місяців тому
Let's hope UA-cam's video re-encoding policy doesn't mess this one up. The satellite wheels indicate the time; the yellow wheel shows the seconds, the green wheel shows the minutes, and the cyan one the hours. The planet wheels are just there to keep everything concentric (and to maintain the whole 'planetary gear' idea). Their number is completely arbitrary, 3 is obviously the minimum, and 4 s...
Mandelbrot to Mandelbar
Переглядів 1,9 тис.9 місяців тому
Morphing the Brot to the Bar, then change the power from 2 to -2, Bar to Brot again, and bringing the power back to 2. I used a binary decomposition for displaying the set, because I felt like it.
20 different methods of inverting the Mandelbrot set
Переглядів 2,1 тис.9 місяців тому
Or: how to get from c to 1/c, and back again. First the cardioid of the main body of the Mandelbrot set is converted to a circle After the inversion the process is reversed so that when a second inversion is applied one gets back to the original image. This instance the sets are displayed by means of a distance estimation method.
Lyapunov Exponents of the series abacbc
Переглядів 1,1 тис.Рік тому
a = 4*sin(2*pi*x) b = 4*cos(2*pi*y) in which x and y are the coordinates of the image. c = 0 to 4, providing the animation
Expanded Mandelbrot set
Переглядів 2,8 тис.Рік тому
The set z = z² dz c, where d is a complex parameter. At d=0 the set reduces to the standard Mandelbrot set that we know and love. The animation has d traversing the Bernoulli Lemniscate in the complex plane, i.e.: Re(d) = cos(phi)/(1 (sin(phi))^2) Im(d) = sin(phi)*cos(phi)/(1 (sin(phi))^2) with phi from pi/2 to 5*pi/2 The set is projected on the 1/c=plane, btw.
Mandelbrot Power Sets aka Multibrot
Переглядів 53 тис.Рік тому
z = z^n c, with n from 2 to 7, to -7 and back to 2. Normally z^n = r^n * exp(n*phi) with r=sqrt(xx yy) and phi=arctan(y/x). In this video z^n = r^n1 * exp(n2*phi) with different choices for n1 and n2 for each frame. Top left: n1=n2=n as standard, other frames n1=1, n1=2n, n1=n/2 etc.
Mandelbrot power sets aka Multibrot sets
Переглядів 23 тис.Рік тому
4 different methods to eponentiate the Mandelbrot set Top left: z^2n c (the generic one) Top right: z^2 c^n Bottom left: z^2n c^n Bottom right: (z^2 c)^n with n from 1 to 5, to -5 and back to 1.
Power morph 4D Mandelbrot cross sections
Переглядів 1,6 тис.Рік тому
This is, for now, my last attempt in exploring the 4D-ness (4D-ity) of the Mandelbrot set, as it exists in (a,b,x0,y0)-space. The lefthand image shows the 3D cross section (a,b,x0) of this 4D set. And the righthand image shows the 3D cross section (a,b,y0). The animation is z=z^n c with n=1..6
Mandelbrot set with complex exponent
Переглядів 7 тис.Рік тому
This is the set z=z^b c, where b is the circle in the complex plane with origin (0,0) and radius 2. The animation is the counterclockwise traversal on this circle. To spice things up a bit, I decided to apply a binary decomposition on the escape radii.
Zoom into Newton's method fractal
Переглядів 2,6 тис.2 роки тому
A quick zoom into Newton's method fractal z = z - p(z) / p'(z) for p(z) = (z-c1)(z-c2)(z-c3), plotting c3-space. c1 = (1,0) and c2 = (-1,0) Based on this video by 3Blue1Brown: ua-cam.com/video/LqbZpur38nw/v-deo.html
Pendulum and magnets experiment in 4D space
Переглядів 1,1 тис.2 роки тому
Another pendulum and magnets chaos experiment, in which the pendulum is suspended in 4D space. The classical pendulum is suspended in 3D space above a 2D plane that holds the magnets. It yields 2D images mapping the starting points to the magnets it ends on. Mathematically there's no problem whatsoever extending this process one dimension higher. So this pendulum is suspended in 4D space and is...
The Mandelbrot set as part of the 4D quadratic formula in 3D
Переглядів 1,2 тис.2 роки тому
The Mandelbrot set as part of the 4D quadratic formula in 3D
The Mandelbrot set as part of the 4D quadratic formula in 3D
Переглядів 7762 роки тому
The Mandelbrot set as part of the 4D quadratic formula in 3D
The Mandelbrot set as part of the 4D quadratic formula
Переглядів 6 тис.2 роки тому
The Mandelbrot set as part of the 4D quadratic formula
Mandelbrot set in fisheye perpective
Переглядів 8 тис.2 роки тому
Mandelbrot set in fisheye perpective
Mandelbrot set projected on a Riemann sphere flattened out to a disc
Переглядів 10 тис.2 роки тому
Mandelbrot set projected on a Riemann sphere flattened out to a disc
Mandelbrot set projected on a flattened out Riemann-sphere
Переглядів 10 тис.2 роки тому
Mandelbrot set projected on a flattened out Riemann-sphere
Mandelbrotset projected on a rotating and shrinking Riemann-sphere
Переглядів 6 тис.3 роки тому
Mandelbrotset projected on a rotating and shrinking Riemann-sphere
Mandelbrot set projected on a shrinking Riemann-Sphere
Переглядів 9 тис.3 роки тому
Mandelbrot set projected on a shrinking Riemann-Sphere
Mandelbrot set projected on a shrinking Riemann-Sphere
Переглядів 13 тис.3 роки тому
Mandelbrot set projected on a shrinking Riemann-Sphere
Mandelbrot set projected on a rotating Riemann-sphere
Переглядів 3,3 тис.3 роки тому
Mandelbrot set projected on a rotating Riemann-sphere
Lyapunov Exponents Animation cbacbacbaa
Переглядів 2,2 тис.3 роки тому
Lyapunov Exponents Animation cbacbacbaa
Lyapunov Exponents Animation bbbacccb
Переглядів 1,7 тис.3 роки тому
Lyapunov Exponents Animation bbbacccb
Lyapunov Exponents Animation of the series (aaabbbccc)
Переглядів 1,4 тис.3 роки тому
Lyapunov Exponents Animation of the series (aaabbbccc)
Lyapunov Exponents Animation of the series (abcacbcabcbabacbca)
Переглядів 1,2 тис.3 роки тому
Lyapunov Exponents Animation of the series (abcacbcabcbabacbca)








At 0:07 you can see that the main cardioid is actually a bulb, or alternatively that all bulbs are technically minibrots
Some of my lost fractals (MbLan/Mandelbrowser): z = conj(z)^2 + 1/z + c (tricorn dust, z0 = c) (z = z^2 + c; z = conj(z)^2+c;) Tribrot z = flip(z)^(flip(2)+flip(c) (Flipbrot, convergence)
0:48 name this fractal
Hey, how dare you hurt my girl? How dare you? That's it? I will grab you. I need to take a bite.
What the heck are you strong for you?What the heck lewin what the heck
Hey you, what can I take a bite?No?Why? I don't said shut up and now
all the maldenbrots expect the second: BOOM!
BRO SCSCSC pls stop spamming
We What the fuck it's a pick up
Hey who dare How far to your hurt you're sister
no no no
someone took half the comments
My sister, my sister, my sister, my sister, my sister, my sister, my sister.Yeah , yeah , yeah , a a a my my sister
What the heck, what the heck?No, my sister, what?No, what?How dare you😊
Is this the hobbit of my sister a happy to my sister
Okay. No no no what happened to my sister😊
Zoom from fractal to Rieman sphere that with the minibrot you go to the bubble above it
Cccccc
What have you done to my sister from my Sis?How will you see your pin that?And you're doing that and freaking calling isaac
Thanks oh so cute
What the what are you doing?No no don't break my sister and my cutie
??????
What the what is this
No, no, no, no, no Lord.Don't you dare
Okay. No, no, no, no, no, no no no, no okay. Okay, I guess I don't forget that.😂😂
No no no
NO IT TURNS TO 3D NOO
Mandelbrowser
0:10
0:30 monobar reverse
One side is the fron, the other is the back
0:07 Monobar
Se is Monobar
This seems like a place to ask...how do I find any information about how the mondelbrot set may be related to spinors?
That's a really interesting question. It could be opening up new areas of investigation, or it could turn out to be trivial. Either way, my knowledge of spinors is not sufficient to say something sensible about the matter.. Hopefully somebody else can. Have you tried posing the question on forums like Quora?
Skbidi hhahahahhha
Fractal wrong!
its 3d
Do you enjoy this thema? But, instead of negotiation with specialists in it, you invent the bycicle again...
I do indeed enjoy this theme, thank you for noticing. Who are the specialists exactly? And how do I get in touch with them?
The hands are excessive
Interesting how such a beautiful thing could be rendered nearly 10 years ago.
Beautiful, thanks for that.
It's really beautiful movie! I suggest you to make NFT from that. It is very likely that someone would buy it for at least 0.2 ETH, maybe more. Good Luck :)
Ooh so that is how "God" sees us? The fabric of spacetime
W I D E
Whas this ChaosPro
This Has No 360°
Left Camera: Back Centre Camera: Sided Right Camera: Front
0:18 19th one *eclipse with glasses 15th without
This Has No 360°
That looks amazing
Thnx!
0:21 spider on the 6th
Mandelbrot zoom in vs Mandelbrot zoom out
🛸Some UFO reports sound similar to 4D objects passing through our space, like morphing rubber blobs that suddenly gain connections or lose connections. Possible clue...
Holographic Holo-Fractal Stochastic Super-Tension Shape Dynamics!.